
-

-

Possibility spaces and the notion of novelty: from music to biology
Synthese
What is a biological novelty? Is it possible to coin a sound concept of new possibility? What articulation between the concepts of novelty and function?
Abstract
We provide a new perspective on the relation between the space of description of an object and the appearance of novelties. One of the aims of this perspective is to facilitate the interaction between mathematics and historical sciences. The definition of novelties is paradoxical: if one can define in advance the possibles, then they are not genuinely new. By analyzing the situation in set theory, we show that defining generic (i.e., shared) and specific (i.e., individual) properties of elements of a set are radically different notions. As a result, generic and specific definitions of possibilities cannot be conflated. We argue that genuinely stating possibilities requires that their meaning has to be made explicit. For example, in physics, properties playing theoretical roles are generic; then, generic reasoning is sufficient to define possibilities. By contrast, in music, we argue that specific properties matter, and generic definitions become insufficient. Then, the notion of new possibilities becomes relevant and irreducible. In biology, among other examples, the generic definition of the space of DNA sequences is insufficient to state phenotypic possibilities even if we assume complete genetic determinism. The generic properties of this space are relevant for sequencing or DNA duplication, but they are inadequate to understand phenotypes. We develop a strong concept of biological novelties which justifies the notion of new possibilities and is more robust than the notion of changing description spaces. These biological novelties are not generic outcomes from an initial situation. They are specific and this specificity is associated with biological functions, that is to say, with a specific causal structure. Thus, we think that in contrast with physics, the concept of new possibilities is necessary for biology.
Keywords: Novelty, Possibility space, Biological functions, Organization, Emergence
Manuscript Citation Publisher Full textCitation
Montévil, Maël. 2019. “Possibility Spaces and the Notion of Novelty: From Music to Biology.” Synthese 196 (11): 4555–81. https://doi.org/10.1007/s11229-017-1668-5 -
No Entailing Laws but Enablement in the Evolution of the Biosphere
-

Why theorization has to make a comeback if we are to meet the challenges of the Anthropocene.
-
Principle of organization, integration of the principles and application — Precision biology: concepts and measurements
Organization constitutes an overarching hypoth- esis that frames the intelligibility of biological objects. We offer a specific characterization of organization in terms of closure of con- straints. The adoption of organization as a principle fosters an orig- inal approach to biological stability. We elaborate on its articulation with the two other theoretical principles addressed in this session and use them to discuss what it means to access empirical objects in biology. Finally, we address measurement and precision in biology.
-

Groupe 1 Epistemology: Anthropocene, exosomatization and negentropy
-
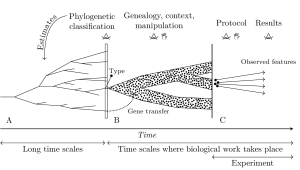
Measurement in biology is methodized by theory
Biology & Philosophy
We characterize measurement in biology from a theoretical perspective with a focus on historicity. We analyze experimental strategies and reproducibility.
Abstract
We characterize access to empirical objects in biology from a theoretical perspective. Unlike objects in current physical theories, biological objects are the result of a history and their variations continue to generate a history. This property is the starting point of our concept of measurement. We argue that biological measurement is relative to a natural history which is shared by the different objects subjected to the measurement and is more or less constrained by biologists. We call symmetrization the theoretical and often concrete operation which leads to considering biological objects as equivalent in a measurement. Last, we use our notion of measurement to analyze research strategies. Some strategies aim to bring biology closer to the epistemology of physical theories, by studying objects as similar as possible, while others build on biological diversity.
Keywords: Biological measurement, evolution, experiments, strains, symmetry, systematics
Manuscript Citation Publisher Full textCitation
Montévil, Maël. 2019. “Measurement in Biology Is Methodized by Theory.” Biology & Philosophy 34 (3): 35. https://doi.org/10.1007/s10539-019-9687-x -
Which first principles for mathematical modelling in biology?
Rendiconti di Matematica e delle sue Applicazioni
Like theoretical physics, theoretical biology is not just mathematical modeling. Instead, it should strive to find principles to frame experiments and models.
Abstract
Like theoretical physics, theoretical biology is not just mathematical modeling. Instead, theoretical biology should strive to find suitable first principles to ground the understanding of biological phenomena and ultimately frame biological experiments and mathematical models. First principles in physics are expressed in terms of symmetries and the associated conservations, on the one side, and optimization on the other side. In biology, we argue instead that a strong notion of variation is fundamental. This notion encompasses new possibilities and the historicity of biological phenomena. By contrast, the relative regularity of some aspects of biological organisms, which we call constraints, should be regarded as the consequence of a mutual stabilization of the parts of organisms. We exemplify several aspects of this framework with the modeling of allometric relationships. Our change of perspective leads to reconsider the meaning of measurements and the structure of the space of description.
Keywords: Allometry, first principles, Historicity, invariants, theoretical biology, Variability
Manuscript Citation Publisher Full textCitation
Montévil, Maël. 2019. “Which First Principles for Mathematical Modelling in Biology?” Rendiconti Di Matematica e Delle Sue Applicazioni 40: 177–89. http://www1.mat.uniroma1.it/ricerca/rendiconti/40_3-4_(2019)_177-189.html



