Ecological Models for Gene Therapy. I. Models for Intraorganismal Ecology
Biological Theory
We discuss the perspective of intra-organismal ecology by investigating a family of models of niche construction. We consider first and second order models.
Abstract
In this article, we discuss the perspective of intraorganismal ecology by investigating a family of ecological models. We consider two types of models. First-order models describe the population dynamics as being directly affected by ecological factors (here understood as nutrients, space, etc). They might be thought of as analogous to Aristotelian physics. Second-order models describe the population dynamics as being indirectly affected, the ecological factors now affecting the derivative of the growth rate (that is, the population acceleration), possibly through an impact on nongenetically inherited factors. Second-order models might be thought of as analogous to Galilean physics. In a companion article, we apply these ideas to a situation of gene therapy.
Keywords: Ecosystem engineering, Inertial dynamics, Intraorganismal ecology, Niche construction, Nongenetic inheritance
Table of contents
Reading time: ~55 min
- Introduction
- 1 First order model
- 2 Second order model
- 3 Model with two species
- 4 Discussion
- References
- 5 Appendices
- 5.1 Model of a limiting maximal per capita growth rate
- 5.2 Linearized monospecific first order system
- 5.3 Linearized monospecific second order system
- 5.4 Linearized two species first order system
- 5.5 Linearized two species second order model (without friction)
- 5.6 Linearized two species second order system (with friction)
- 5.1 Model of a limiting maximal per capita growth rate
Ecological models for gene therapy 1: models for intraorganismal ecology
Abstract
In this paper, we discuss the perspective of intra-organismal ecology by investigating a family of ecological models. We consider two types of models. First order models describe the population dynamics as being directly affected by ecological factors (here understood as nutrients, space, etc). They might be thought of as analogous to Aristotelian physics. Second order models describe the population dynamics as being indirectly affected, the ecological factors now affecting the derivative of the growth rate (that is, the population acceleration), possibly through an impact on non-genetically inherited factors. Second order models might be thought of as analogous to Galilean physics.
In the joint paper, we apply these ideas to a situation of gene therapy.
Keywords: Intra-organismal ecology
Introduction
The organism can be seen as a biome, composed of organs that are ecosystems where are played ecological and evolutionary drama Kupiec and Sonigo (2003).
This perspective draws back to the speculations of Roux (1881) and Weismann (1904)[1]) on selection occurring inside the organism. More recently, eco-evolutionary processes between cells within an organism have been considered, both to explain the existence of protection mechanisms against the proliferation of cancer cells within an organism Cairns (1975); Nowak et al ( 2003), to predict the spread of resistant phenotypes within cell populations during cancer treatments Nowell (1976); Merlo et al (2006), to describe intra-host dynamics of infectious diseases or cancers as predator-prey interactions between viruses and the immune system Nowak and May (2000); Merlo et al (2006)[2], or to apply the neutral theory of biodiversity Hubbell (2001) to gut or skin flora communities (e.g. Turnbaugh et al (2007); Roth and James (1988, 1989)).
This paper takes place in such an intra-organismal eco-evolutionary perspective. The topic we are interested in is the study of a gene therapy. Gene therapy aims at correcting a physiological dysfunction whose origin is the inadequate expression of a defective gene. In practice, patient cells are genetically modified in vitro by inserting a given gene, and then re-injected to the patient, with the aim that these modified cells replace the resident cells, or at least that they durably persist within patient’s body: that is, that cells be successfully engrafted Aiuti and Giovannetti ( 2003); Cavazzana-Calvo et al (2005). From an ecological point of view, the prospective replacement of a cellular strain by another is similar to a competitive exclusion or a drift, while modification of the cellular environment, for instance by producing a missing enzyme, is similar to ecosystem engineering Jones et al (1994) or, in other terms, to niche construction (Odling-Smee et al ( 2003), chap.5)[3]. Successful or unsuccessful engraftment qua species invasion will then depend on the details of the ecological interaction Gonzalez et al ( 2008). The aim of the present work is to determine the conditions of successful engraftment.
To this aim, we will study a family of ecological models describing the dynamics of cell populations within an organism. In the first part, we will present the family of models of competition between cells in the general, non-pathological, case. This will enable us to more easily discuss those aspects of the models that are not limited to the particular case of gene therapy.
General model of cell population dynamics
We consider that cells proliferate inasmuch as limiting constraints enable them to. More specifically, we will assume here that the population dynamics directly depends from a limiting factor
1 First order model
We consider that the limiting factor
| | (1) |
where
Equation 1 admits one (stable) equilibrium:
| |
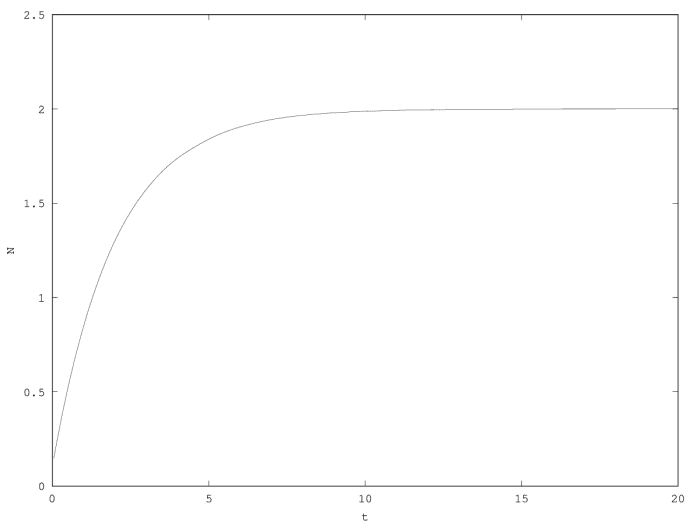
The system relaxes towards the equilibrium with a characteristic time
| |
From then on, we consider only the case where
2 Second order model
We now turn to a different type of modeling, following the works of Ginzburg and colleagues on demographic inertia Ginzburg et al (2004). We consider that the per capita growth rate now shows a certain inertia (comparable to inertia in Newtonian physics) that is perceptible at the scale of population dynamics. Put it differently, we will not separate the time-scales of the per capita growth rate dynamics and of the population dynamics.
From the biological point of view, such an inertia in the per capita growth rate can result from a dynamics in cell quality (e.g., available amount of intracellular resources or organization quantity, sensu Bailly and Longo (2009)). Then, if environmental conditions worsen, intracellular resources lead to a delay in the demographic response; conversely if living conditions get better the cells first rebuild their intracellular resources before their demographic parameters (division and mortality) get affected. Individual quality can also be transmitted to offspring, a phenomenon known in ecology as maternal effects (e.g. Mousseau and Fox (1998)).
In this model, it is the change of the per capita growth rate that depends on the per capita limiting factor
| | (2) |
The model is formally similar to the first order model, but notice that the dimensionality and the meaning of the variables has now changed. The equilibrium of equation 2 results when
2.1 A note on the analogy with physics
In this model, demographic factors (
According to equation 2, in the idealized case where
Our interpretation of demographic inertia departs from Ginzburg’s here Ginzburg et al (2004) (chap.6), who consider that the default state of dynamics is the absence of limiting factors (i.e.
By contrast, we consider here that the metabolism
Contrary to Newtonian physics however where the default state is general, the idealized equation 2 where all factors are put to zero can make sense only in very special cases where cell quality is fully heritable during divisions (e.g. some environment sensitive epigenetic marks), that is, it does not hold for intracellular resources that are shared among daughter cells. Below we will consider the impact of resource sharing among offspring, and see how it radically modifies the dynamics
2.2 Differences between inertial and non-inertial dynamics: accelerated death, overshoot
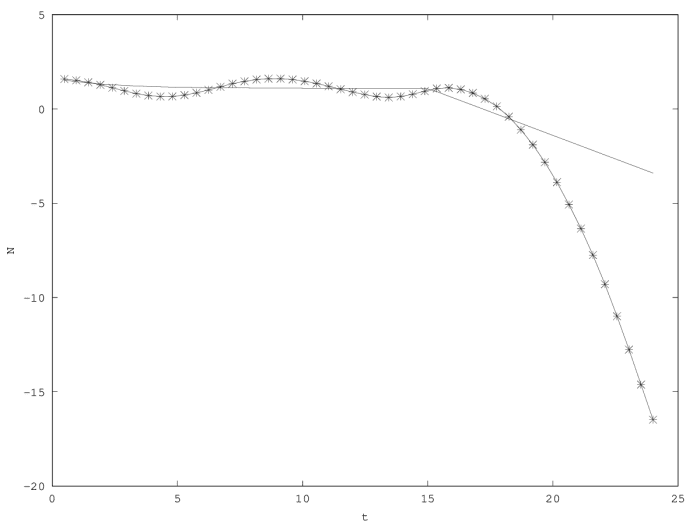
In the inertial model (equation 2), death is accelerated when the limiting factor is the strongest (i.e. set to zero): the per capita growth rate decreases and can tend towards
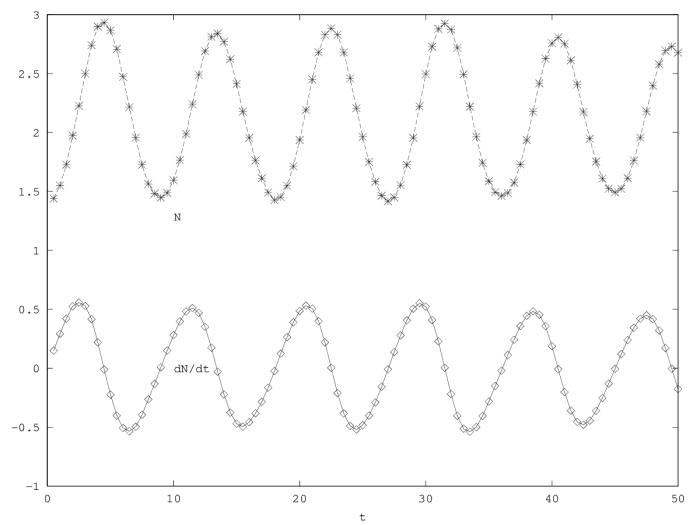
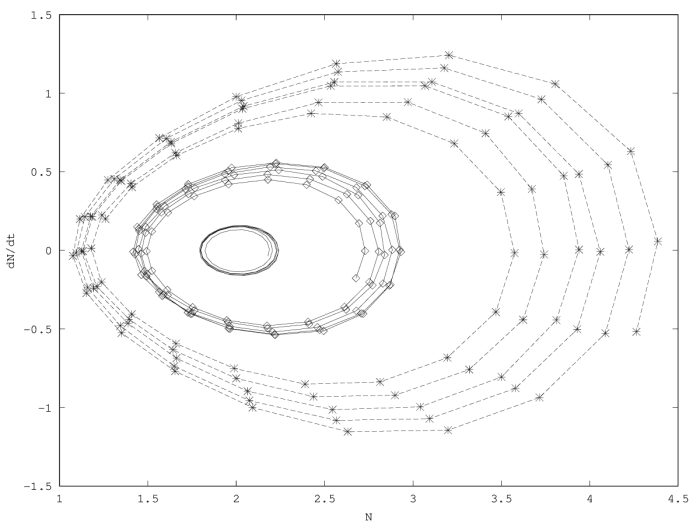
An inertial dynamics also allows to overshoot the demographic equilibrium value of the population (figure 2.2, figure 2.2). Overshoot leads to demographic oscillations around the equilibrium value with a pulsation
2.3 Friction, antifriction
In the model described by equation 2, oscillations around the equilibrium value are neither damped nor amplified. Such a behavior is structurally unstable: small modifications of the model lead to the convergence toward stable equilibrium or to divergence May (1973); Nowak and May ( 2000).
From a biological point of view, oscillations are damped when good quality cells (
| | (3) |
Equation 3 cancels out when
| |
In particular, in the case of a free fall (
Ginzburg et al (2004) p90 also modeled population dynamics with a second order equation (that is, with
Close to the equilibrium, the system with friction (
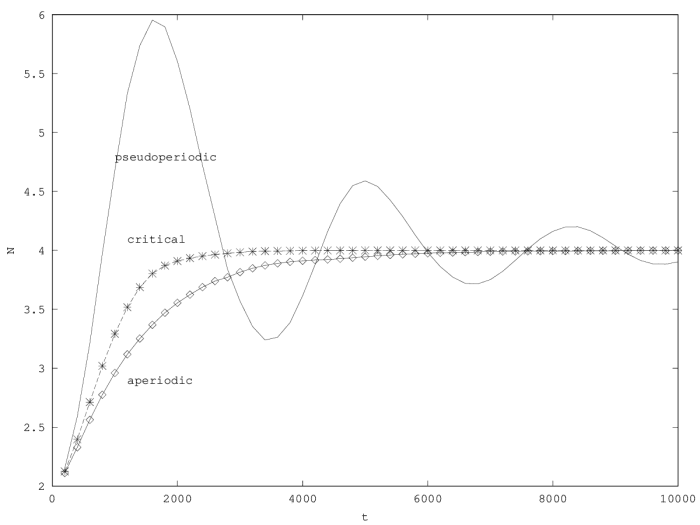
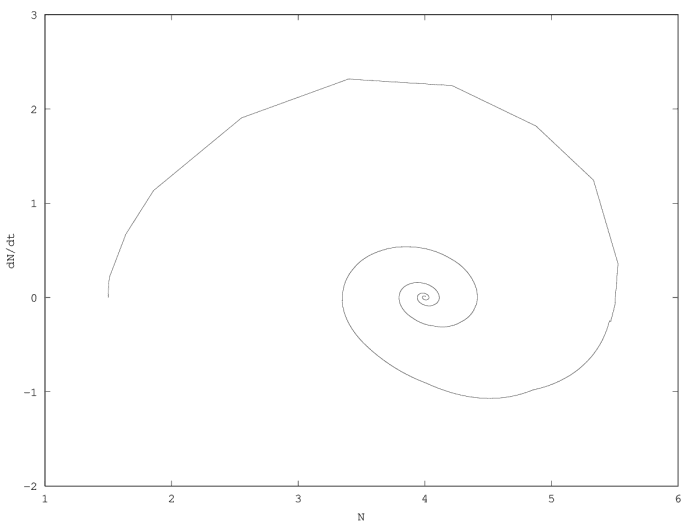
- pseudoperiodical regime with damped oscillations (
The period is given by
- critical regime (
- aperiodical regime (
Note that relaxation is slower than in the damped oscillation regime, because now friction also opposes to the return to equilibrium.
We will see how, from a theoretical point of view, the existence of friction in cell population dynamics can have therapeutic implications.
3 Model with two species
In this section we derive the models of sections 1.1 and 1.2 to describe the case of an interaction between two species (in our case, two cellular strains). These are the models we will use in the next part. Though we describe the dynamics from a general point of view in this section (that is, without making any symmetry assumption about the species in presence) we will be able to drastically reduce the number of parameters in the following part assuming that the cellular strains (genetically modified and non-modified) are identical in most respect.
3.1 First order model
We suppose that the two species interact in a competitive way via their dependency to the limiting factor
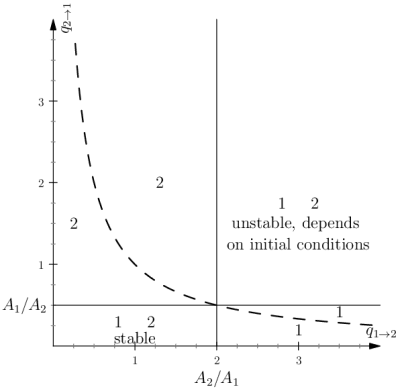
The behavior of the system, and in particular the stability of the equilibra in the space of parameters is shown in figure 3.1. The system has three equilibria: two equilibria correspond to the loss of a least one species and reduce to the monospecific case, one corresponds to the coexistence between populations
(a)
(b) the equilibrium corresponding to coexistence is given by the couple
The equilibrium is a coexistence iff
3.2 Second order model
We similarly extend the second order monospecific model to the two-species case by doing the same assumptions about the competitive interaction between 1 and 2:
The equilibrium of this system obtains for the same equilibrium values than the first order system (steady
3.3 Second order model with friction
We now add friction to the two-species model:
From then on, we will only consider cases where
4 Discussion
A model of population dynamics should exhibit three essential behaviors: decline in absence of resources, growth in non-limiting situations (
It is impossible to represent the possible actions on these three independent behaviors with only two parameters (e.g.,
Under these constraints, and to favor parsimony which is essential to our application on gene therapy (next section), we have sacrificed the behavior of the population far from the
| |
or in the version of Lotka (1925):
| |
We did not choose this model for the following reasons:
- The difficulty of interpreting the parameters Olson (1992). First,
- The unrealistic form of the density dependence Getz (1996), when
We have chosen here to model the dynamics for situations where
In this work, we limited ourselves to the ecological dimension of the cellular niche, that is, to the impact of density on competition. However, in intra-organismal ecology density-dependence has effect that are unknown in organism ecology. Physical constraints, in particular, are known to affect the differentiation of stem cells in given niches Gerecht-Nir et al (2004); Mohr et al (2006); Stevens et al (2007) as well as to affect the malignant phenotype and the response to treatments in the case of cancer Ingber and Jamieson (1985); Huang and Ingber ( 2005); Paszek et al (XXXX) and Schwartz ( 2004) chap.15. This is a new behavior by comparison with organism ecology, where the most similar behaviors would be migration and metamorphosis[9].
Last, in classical population ecology, populations, once lost, do not reappear if there is no migration nor dormant propagule bank in the environment. Thus,
The model being simple and basically describing a relaxation toward an equilibrium (at the first order, or at the second order with friction), some structural homogeneity is expected with existing models in the literature. We can notice in particular a certain formal homology (partial, except in cases where we introduce a
In this work, we focused on the structural stability of our modeling, by introducing a friction term. A strong friction makes the system tend towards a first order behavior: inertia loses its dynamical importance. In the general models presented above, friction affects relaxation but not the equilibrium stability. This will not be the case in the next section anymore.
Our model shows how the same equational form can be interpreted at the first or the second order (keeping in mind that the dimension and the meaning of the parameters change according to the order). At the first order, the system describes the growth of an organ, or, in the model with two species, the potential invasion of an organ by a cellular strain. At the second order, our model is structurally identical to that of Ginzburg et al (2004) p44 modeling the quality of individuals. This structural homology between first and second order enables to study the importance of the time-scale separation hypotheses between the individual’s quality (
The diversity of empirical results in population dynamics makes it difficult to a priori choose between the first and second order models. Qualitative results of the first order model are in concordance with some empirical results as regards the growth of an organ or of the quality of a cell (see e.g. resp. Kooijman (2000) p33:fig.2.5 and p2:fig.1.1). However the second order model is in concordance with demographic oscillations (damped, amplified, or not) and accelerated death observed in organism ecology (see the review by Ginzburg et al (2004) p92-93), and in intra-organismal ecology (Corbin et al ( 2002), see also companion paper).
Acknowledgements: This work is based on notes written up by Regis Ferrière in 2004 after a project started at the CEMRACS 2004, whose participants were Antonio Cappucio, Etienne Couturier, Michel de Lara, Regis Ferriè re, Olivier Sester, Pierre Sonigo, Christian et Carlo. The authors also whish to thank the organizers and participants of the StabEco workshop, held at the Laboratory Ecology and Evolution, University of Paris 6, on the 17/12/2010. Philippe Huneman and Minus van Baalen provided invaluable comments on earlier versions of the manuscript.
This work consists in an update of a previous work in French Pocheville ( 2010), chap. 3, realized while both A.P and M.M. were benefiting from a funding from the Frontiers in Life Sciences PhD Program and from the Liliane Bettencourt Doctoral Program. Manuscript was written while A.P was benefiting from a Postdoctoral Fellowship from the Center for Philosophy of Science, Uni- versity of Pittsburgh. M.M. is currently benefiting from a Postdoctoral Fellowship from the Region Ile-de-France, DIM-ISC.
References
- Aiuti F, Giovannetti A (2003) Structured interruptions of therapy: looking for the best protocol. Aids 17(15):2257–2258
- Akçakaya H, Ginzburg L, Slice D, Slobodkin L (1988) The theory of population dynamics—ii. physiological delays. Bulletin of Mathematical Biology 50(5):503–515
- Akçakaya HR, Arditi R, Ginzburg LR (1995) Ratio-dependent predation: an abstraction that works. Ecology pp 995–1004
- Alizon S, van Baalen M (2008) Multiple infections, immune dynamics, and the evolution of virulence. The American Naturalist 172(4):E150–E168
- Alizon S, Hurford A, Mideo N, Van Baalen M (2009) Virulence evolution and the trade-off hypothesis: history, current state of affairs and the future. Journal of evolutionary biology 22(2):245–259
- Arditi R, Ginzburg LR (1989) Coupling in predator-prey dynamics: ratio-dependence. Journal of Theoretical Biology 139(3):311–326
- Bach LA, Bentzen S, Alsner J, Christiansen FB (2001) An evolutionary-game model of tumour–cell interactions: possible relevance to gene therapy. European Journal of Cancer 37(16):2116–2120
- Bailly F, Longo G (2009) Biological organization and anti-entropy. Journal of Biological Systems 17(01):63–96
- Bailly F, Longo G, Montévil M (2011) A 2-dimensional geometry for biological time. Progress in biophysics and molecular biology 106(3):474–484
- Berryman AA (1992) The origins and evolution of predator-prey theory. Ecology 73(5):1530–1535
- Beverton R, Holt S (1957) On the dynamics of exploited fish populations. fisheries investigation series 2, vol. 19, uk ministry of agriculture. Fisheries, and Food, London
- Billy F, Ribba B, Saut O, Morre-Trouilhet H, Colin T, Bresch D, Boissel JP, Grenier E, Flandrois JP (2009) A pharmacologically based multiscale mathematical model of angiogenesis and its use in investigating the efficacy of a new cancer treatment strategy. Journal of theoretical biology 260(4):545–562
- Brawley C, Matunis E (2004) Regeneration of male germline stem cells by spermatogonial dedifferentiation in vivo. Science 304(5675):1331–1334
- Brown SP, Le Chat L, Taddei F (2008) Evolution of virulence: triggering host inflammation allows invading pathogens to exclude competitors. Ecology letters 11(1):44–51
- Cairns BJ, Timms AR, Jansen VA, Connerton IF, Payne RJ (2009) Quantitative models of in vitro bacteriophage–host dynamics and their application to phage therapy. PLoS pathogens 5(1):e1000,253
- Cairns J (1975) Mutation selection and the natural history of cancer. Nature 255:197–200
- Cavazzana-Calvo M, Lagresle C, Hacein-Bey-Abina S, Fischer A (2005) Gene therapy for severe combined immunodeficiency. Annu Rev Med 56:585–602
- Corbin IR, Buist R, Volotovskyy V, Peeling J, Zhang M, Minuk GY (2002) Regenerative activity and liver function following partial hepatectomy in the rat using 31p-mr spectroscopy. Hepatology 36(2):345–353, doi: 10.1053/jhep.2002.34742
- Courchamp F, Clutton-Brock T, Grenfell B (1999) Inverse density dependence and the allee effect. Trends in ecology & evolution 14(10):405–410
- Dingli D, Offord C, Myers R, Peng K, Carr T, Josic K, Russell S, Bajzer Z (2009) Dynamics of multiple myeloma tumor therapy with a recombinant measles virus. Cancer gene therapy 16(12):873–882
- Etienne R, Wertheim B, Hemerik L, Schneider P, Powell J (2002) The interaction between dispersal, the allee effect and scramble competition affects population dynamics. Ecological Modelling 148(2):153–168
- Fu X, Sun X, Li X, Sheng Z (2001) Dedifferentiation of epidermal cells to stem cells in vivo. The lancet 358(9287):1067–1068
- Gerecht-Nir S, Cohen S, Ziskind A, Itskovitz-Eldor J (2004) Three-dimensional porous alginate scaffolds provide a conducive environment for generation of well-vascularized embryoid bodies from human embryonic stem cells. Biotechnology and bioengineering 88(3):313–320
- Getz WM (1996) A hypothesis regarding the abruptness of density dependence and the growth rate of populations. Ecology 77(7):2014–2026
- Getz WM, Kaitala V (1989) Ecogenetic models, competition, and heteropatry. Theoretical Population Biology 36(1):34–58
- Ginzburg L, Akçakaya H, Slice D, Slohodkin L (1988) Balanced growth rates vs. balanced accelerations as causes of ecological equilibria. In: Biomathematics and Related Computational Problems, Springer, pp 165–175
- Ginzburg LR, Colyvan M, et al (2004) Ecological orbits: how planets move and populations grow. Oxford University Press New York
- Gonzalez A, Lambert A, Ricciardi A (2008) When does ecosystem engineering cause invasion and species replacement? Oikos 117(8):1247–1257
- Gould SJ (2002) The structure of evolutionary theory. Harvard University Press
- Huang S, Ingber DE (2005) Cell tension, matrix mechanics, and cancer development. Cancer cell 8(3):175–176
- Hubbell SP (2001) The unified neutral theory of biodiversity and biogeography (MPB-32), vol 32. Princeton University Press
- Ingber D, Jamieson J (1985) Cells as tensegrity structures: Architectural regulation of histodifferentiationby physical forces tranduced over basement membranes. Gene Expression during Normal and Malignent Differentiation
- Jacobs F, Metz J (2003) On the concept of attractor for community-dynamical processes i: the case of unstructured populations. Journal of mathematical biology 47(3):222–234
- Jones CG, Lawton JH, Shachak M (1994) Organisms as ecosystem engineers. In: Ecosystem Management, Springer, pp 130–147
- Kent A, Patrick Doncaster C, Sluckin T (2003) Consequences for predators of rescue and allee effects on prey. Ecological Modelling 162(3):233–245
- Kooijman SALM (2000) Dynamic energy and mass budgets in biological systems. Cambridge University Press
- Kupiec JJ, Sonigo P (2003) Ni Dieu ni gène: pour une autre théorie de l’h érédité. Editions du Seuil
- Mac Gabhann F, Annex BH, Popel AS (2010) Gene therapy from the perspective of systems biology. Current opinion in molecular therapeutics 12(5):570
- May RM (1973) Stability and complexity in model ecosystems. Princeton University Press
- Maynard Smith J, Slatkin M (1973) The stability of predator-prey systems. Ecology 54(2):384–391
- McCarthy M (1997) The allee effect, finding mates and theoretical models. Ecological Modelling 103(1):99–102
- Merlo LM, Pepper JW, Reid BJ, Maley CC (2006) Cancer as an evolutionary and ecological process. Nature Reviews Cancer 6(12):924–935
- Mohr JC, de Pablo JJ, Palecek SP (2006) 3-d microwell culture of human embryonic stem cells. Biomaterials 27(36):6032–6042
- Mousseau TA, Fox CW (1998) The adaptive significance of maternal effects. Trends in Ecology & Evolution 13(10):403–407
- Murray JM, Fanning GC, Macpherson JL, Evans LA, Pond SM, Symonds GP (2009) Mathematical modelling of the impact of haematopoietic stem cell-delivered gene therapy for hiv. The journal of gene medicine 11(12):1077–1086
- Niwa H, Miyazaki Ji, Smith AG (2000) Quantitative expression of oct-3/4 defines differentiation, dedifferentiation or self-renewal of es cells. Nature genetics 24(4):372–376
- Novozhilov AS, Berezovskaya FS, Koonin EV, Karev GP, et al (2006) Mathematical modeling of tumor therapy with oncolytic viruses: regimes with complete tumor elimination within the framework of deterministic models. Biology Direct 1(6):18
- Nowak M, May RM (2000) Virus Dynamics: Mathematical Principles of Immunology and Virology: Mathematical Principles of Immunology and Virology. Oxford university press
- Nowak MA, Michor F, Iwasa Y (2003) The linear process of somatic evolution. Proceedings of the National Academy of Sciences 100(25):14,966–14,969
- Nowell PC (1976) The clonal evolution of tumor cell populations. Science 194(4260):23–28
- Odling-Smee FJ, Laland KN, Feldman MW (2003) Niche construction: the neglected process in evolution. 37, Princeton University Press Olson M (1992) Intuition and the logistic equation. Trends Ecol Evol 7:314
- Paszek MJ, Zahir N, Johnson KR, Lakins JN, Rozenberg GI, Gefen A, Reinhart-King CA, Margulies SS, Dembo M, Boettiger D, Hammer DA, Weaver VM (XXXX) Tensional homeostasis and the malignant phenotype. Cancer Cell 8(3):241–254, doi: 10.1016/j.ccr.2005.08.010, URL http://www.cell.com/cancer-cell/abstract/S1535-6108(05)00268-0
- Phillips AN (1996) Reduction of hiv concentration during acute infection: independence from a specific immune response. Science 271(5248):497–499
- Piraino S, Boero F, Aeschbach B, Schmid V (1996) Reversing the life cycle: medusae transforming into polyps and cell transdifferentiation in turritopsis nutricula (cnidaria, hydrozoa). Biological Bulletin pp 302–312
- Pocheville A (2010) La Niche Ecologique: Concepts, Modèles, Applications (PhD thesis). URL http://hal.upmc.fr/tel-00715471/
- Roth RR, James WD (1988) Microbial ecology of the skin. Annual Reviews in Microbiology 42(1):441–464
- Roth RR, James WD (1989) Microbiology of the skin: resident flora, ecology, infection. Journal of the American Academy of Dermatology 20(3):367–390
- Roux W (1881) Der kampf der theile im organismus.
- W. Engelmann Schwartz L (2004) Cancer: Between glycolysis and physical constraint. Springer
- Shen CN, Slack JM, Tosh D (2000) Molecular basis of transdifferentiation of pancreas to liver. Nature Cell Biology 2(12):879–887
- Stevens NR, Raposo AA, Basto R, St Johnston D, Raff JW (2007) From stem cell to embryo without centrioles. Current Biology 17(17):1498–1503
- Tayi VS, Bowen BD, Piret JM (2010) Mathematical model of the rate-limiting steps for retrovirus-mediated gene transfer into mammalian cells. Biotechnology and bioengineering 105(1):195–209
- Turnbaugh PJ, Ley RE, Hamady M, Fraser-Liggett C, Knight R, Gordon JI (2007) The human microbiome project: exploring the microbial part of ourselves in a changing world. Nature 449(7164):804
- Watkinson A (1992) Plant senescence. Trends in ecology & evolution 7(12):417–420
- Weismann A (1904) Vorträge über Deszendenztheorie: gehalten an der Universit ät zu Freiburg im Breisgau. G. Fischer
- Weismann A, Thomson JA, Thomson MR (1904) The evolution theory, vol 1.
- Edward Arnold Winsor CP (1932) The gompertz curve as a growth curve. Proceedings of the National Academy of Sciences of the United States of America 18(1):1
5 Appendices
5.1 Model of a limiting maximal per capita growth rate
Let’s start from equation 1:
| |
Here the per capita growth rate tends toward infinity when N(t)/
| | (10) |
where b is a scale constant (number of cells by limiting factor units) introduced to describe the behavior of the per capita growth rate at small cell densities.
The equation for the maximal per capita growth rate
| |
This equation describes
The population tends towards an equilibrium value
| |
Thus a condition on
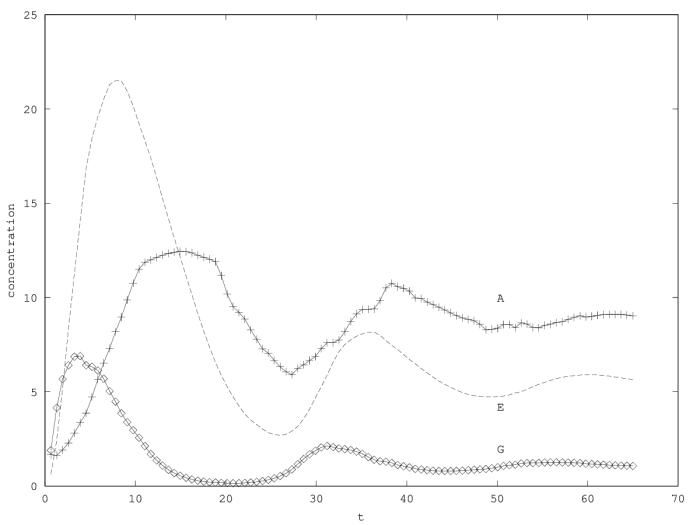
The behavior of model (1 bis) is very similar to the classical logistic model (figure 5.1).
5.2 Linearized monospecific first order system
See the two species system, with
5.3 Linearized monospecific second order system
We have:
| |
We can write the equation in function of
| |
The equilibrium obtains:
| |
We consider the behavior near this equilibrium, that is
| |
Changing the variable:
| |
We obtain:
| |
Noting
If
| |
| |
The pulsation is given by
If
| |
| |
If
| |
| |
The pseudo-pulsation is given by
5.4 Linearized two species first order system
| |
| |
Near the equilibrium, we write:
| |
| |
We get:
| |
Rearranging, we get:
| |
And:
| |
We seek for the eigenvalues of this system. They are the roots of the characteristic polynomial:
We set:
| |
| |
With this parameters, we get:
| |
| |
The determinant
| |
Thus :
| |
Thus
Thus the eigenvalues are :
| |
and:
| |
| |
It turns out that
When
If
If
In the case where
5.5 Linearized two species second order model (without friction)
The calculus is identical to the first order system, but the interpretation differs.
When
If
5.6 Linearized two species second order system (with friction)
We consider the case where
| |
where
| |
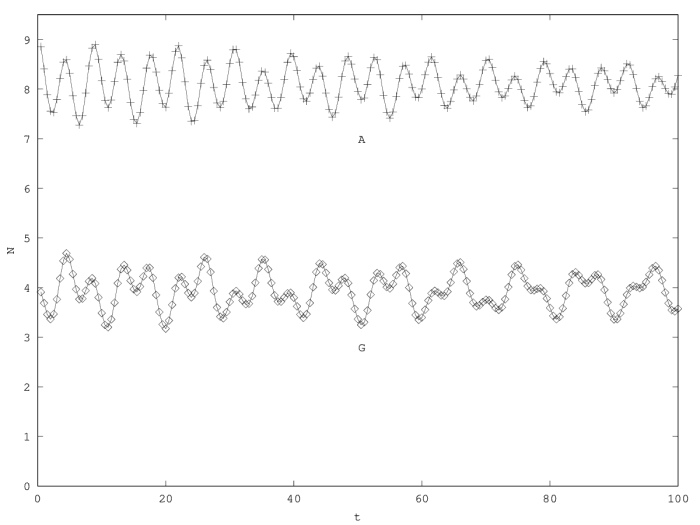
If
If
If