Ecological Models for Gene Therapy. II. Niche Construction, Nongenetic Inheritance, and Ecosystem Perturbations

Ecological models for gene therapy 2: niche construction, non-genetic inheritance, and ecosystem perturbations

Keywords: Intra-organismal ecology; niche construction; ecosystem engineering; non-genetic inheritance; inertial dynamics; gene therapy; adenosine deaminase deficiency; severe combined immunodeficiency; ADA-SCID

Introduction

In this second article, we will study the impacts of niche construction by genetically modified cells on cell populations dynamics. This will enable us to propose some recommendations and new empirical questions to the practitioner. We will show that the conclusions will depend on sensitive hypotheses on time-scale separation (or entanglement) of the considered cellular processes. We will then discuss how ecological concepts can be implemented in cell biology in general, and how extending ecology to cell biology can in turn enrich ecological questions.

Our biological model is the deficiency in adenosine deaminase (ADA), a rare monogenic disease (occurrence between 1:300 000 and 1:1 000 000) Cavazzana-Calvo et al (2004, 2005). From a biochemical point of view, ADA deficiency causes a dysfunction of the metabolism of purines characterized by the accumulation of metabolites in intra- and inter-cellular compartments, which results in particular in a premature apoptosis of lymphocytes Cavazzana-Calvo et al (2005). The lymphocyte anomaly is still not completely elucidated Gaspar et al (2009). ADA deficiency leads to severe anomalies in the immune system (that is, SCID: severe combined immunodeficiency), as well as to other systemic problems, and without treatment the disease is fatal within the first year. Three kinds of treatments are possible: hematopoietic stem cell transplantation (HSCT), enzyme injection, and gene therapy. Hematopoietic stem cell transplantation represents a good option if and only if a related and compatible donor is available (88% survival after one year, vs. 29% and 67% in the case of non-compatible or non-related donors respectively). Enzyme injection takes place every one or two weeks, using polyethylene-glycol bovine adenosie deaminase (PEG-ADA), and enables to maintain a high level of plasmatic ADA, but the restoration of the immune function is suboptimal in the long term. Last, gene therapy enables to restore the immune and metabolic function, with a complete restoration in the best cases, even without preliminary myeloablation Aiuti and Giovannetti (2003); Aiuti et al (2007)^[1]

When a patient, who is initially receiving enzyme therapy, receives an injection of modified cells within a gene therapy, there is a trade-off between continuing the enzyme treatment that enables to maintain a high level of plasmatic ADA, and discontinuing the enzyme treatment with the aim of procuring a selective advantage to modified cells, possibly due to their own enzyme production, to favor engraftment Aiuti et al (2002b)^[2]. The modeling aim of the present work is to investigate the conditions for engraftment from an intra-organismal point of view and the impact enzyme injections can have on cell population dynamics.

1 First order model

We now modify the general first order system (Equations 4-5, first article) to model in particular the intra-organismal ecological dynamics of a ADA-SCID gene therapy (see introduction). We consider that non-modified cells (i.e. the autochthons, hereafter noted $A$) and the genetically modified cells (noted $G$) are identical, except with respect to the construction of the environment (by enzyme synthesis) and the response to the enzyme (noted $E$). All cells are in competition for the limiting factor $\phi$.

G cells are supposed to have a normal dynamics Cassani et al (2009), as described by Equation 4 (first article). To facilitate model interpretation, we separate the cost of enzyme production (noted c) from the intrinsic mortality (m),

$$\frac{dG}{Gdt}=\frac{a\phi }{A+G}-m-c$$

A cells follow the same dynamics than G cells, but they do not pay the cost of enzyme production. In contrast, when the enzyme is missing in the environment, A cells undergo an additional mortality d due to the accumulation of intracellular metabolites. The presence of the enzyme lowers the additional mortality, times a scale factor denoted b. We consider that A cell detoxification by the enzyme depends on the enzyme plasmatic concentration, and not on the per capita quantity, which is assumed to be negligibly modified by the interaction with A cells^[3]. Notice that now, the model is not scale-independent anymore: multiplying the quantity G, A, E by a given factor will lower the additional mortality of A due to the increase in enzyme concentration. The dynamics for A becomes:

$$\frac{dA}{Adt}=\frac{a\phi }{A+G}-m-\frac{d}{1+bE}$$

(1)

The enzyme undergoes an intrinsic decay (with a characteristic time ${\tau }_E$), and is synthesized by $G$ cells, times an “engineering” factor (in reference to ecosystem engineering), denoted $e$. The enzyme can also be injected in a given quantity $i$. The injection frequency (once or twice a week) is of the same order of magnitude as the cell generation time (ca. five days). If injections were more sporadic, $i$ should be replaced by a Dirac comb $i\left(t\right)$.

$$\frac{dE}{dt}=\frac{-1}{{\tau }_E}E+i+eG$$

This system admits several equilibria (the stability conditions are discussed below):

1. In absence of both $A$ and $G$ cells, $E^{\ast }=i{\tau }_E$

This biological equilibrium describes the state of the system in case of a myeloablation, before the injection of modified cells.

1. $G\ast =0$, $E\ast =i{\tau }_E$ and :

$$A^{\ast }=\frac{a\phi }{m+\frac{d}{1+bi{\tau }_E}}$$

This is the hypothetical equilibrium before gene therapy or after $G$ cells have been eliminated if the graft fails.

1. $A\ast =0$, and:

$$G^{\ast }=\frac{a\phi }{m+c}$$

$$E^{\ast }={\tau }_E\left(i+e\frac{a\phi }{m+c}\right)$$

This is the therapeutic target equilibrium, where $A$ cells have been replaced by functionally supplemented $G$ cells.

1. $A\ast \ne 0$, $G\ast \ne 0$, then:

$$E^{\ast }=\frac{1}{b}\left(\frac{d}{c}-1\right)$$

$E>0$ when $d>c$. If $d<c$, there is no coexistence: non-modified autochthons always win. From a biological point of view, $d<c$ would mean that even in the absence of enzyme, the additional mortality of defective non-modified cells is inferior to the cost of producing the enzyme. If there is coexistence, the equilibrium is stable. Knowing $E\ast$ gives $G\ast$ :

$$G^{\ast }=\frac{1}{e}\left(\frac{E^{\ast }}{{\tau }_E}-i\right)$$

Substituting the value of $E^{\ast }$ in $G^{\ast }$, we find that $G^{\ast }>0$ when:

$$\frac{1}{b{\tau }_E}\left(\frac{d}{c}-1\right)>i$$

If $i$ is too large, the inequality is not satisfied and $G^{\ast }$ < 0. From a biological point of view, this means that above a certain injection threshold, engraftment is impossible. We find here the behavior empirically observed by Aiuti et al (2002b).

Knowing $G^{\ast }$:

$$A^{\ast }=\frac{a\phi }{m+c}-G^{\ast }$$

$A^{\ast }>0$ when $a\phi ∕(m+c)>G^{\ast }$ : the coexistence between $A$ and $G$ is not scale-independent, that is, it depends on the carrying capacity of the system (this comes for the scale-dependence introduced by the enzyme concentration).

We can notice that at this equilibrium, the enzyme concentration $E^{\ast }$ does not depend on the injection constant $i$: enzyme injection has merely the effect of decreasing $G^{\ast }$, because of competition with non-modified $A$ cells (also observed by Aiuti et al (2002b)). From a therapeutical point of view, enzyme injection is thus counterproductive at the equilibrium.

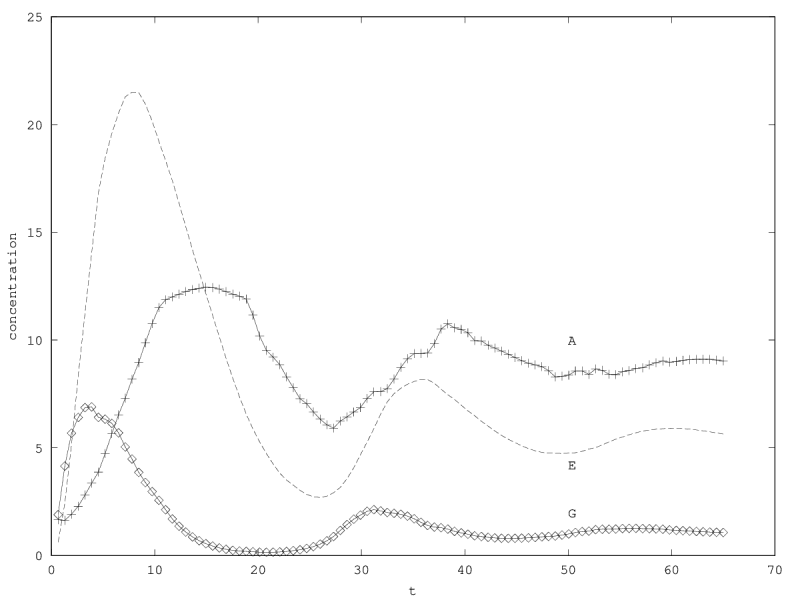
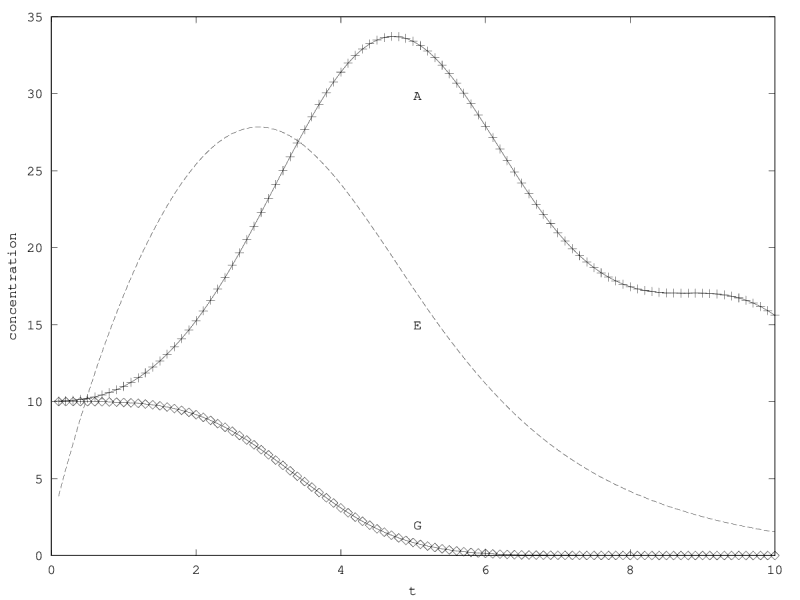
When there is coexistence, the system follows a regime of exponential relaxation, or a pseudoperiodical regime with damped oscillations (figure 1), or is unstable (see appendix 5.1). These oscillations result from the coupling of $A$ and $G$ population via the enzyme compartment, that itself has some inertia, with a characteristic time ${\tau }_E$.

2 Second order model

In this section, we modify the first-order model into a second-order model following the reasoning exposed for the general model, to be able to investigate the therapeutic impacts of a potential time-scale non-separability between the per capita growth rate dynamics ( $dr∕dt$) and the population dynamics ( $dN∕Ndt=r$). The second order system is given by:

$$\frac{dr{}_A}{dt}=\frac{a\phi }{A+G}-m-\frac{d}{1+bE}$$

$$\frac{dr{}_G}{dt}=\frac{a\phi }{A+G}-m-c$$

The equation for enzyme dynamics is as before:

$$\frac{dE}{dt}=\frac{-1}{{\tau }_E}E+i+eG$$

This system admits the same equilibria as the first order system, but its behavior in the neighborhood of the equilibria is different.

If the enzyme dynamics is fast compared to the population dynamics, we may approximate $E$ by ${\tau }_E(i+eG)$. (In ecological terms, this amounts to suppose that $G$ cells do not have any posthumous phenotypes, sensu Lehmann (2008).) The system has the same equilibria. Linearizing near the equilibrium, it turns out that the system can either oscillate around the equilibrium, or diverge with amplified oscillations (see appendix 5.2). Injection quantity $i$ can destabilize the system when $d(m+c)<4c^2$. However, if we consider that coexistence occurs when $d>c$, and that, a priori, $m\gg c$ (that is, synthesizing the enzyme is only a minor fraction of the metabolic work of a $G$ cell), such a destabilization is not expected to occur except for extreme parameters values.

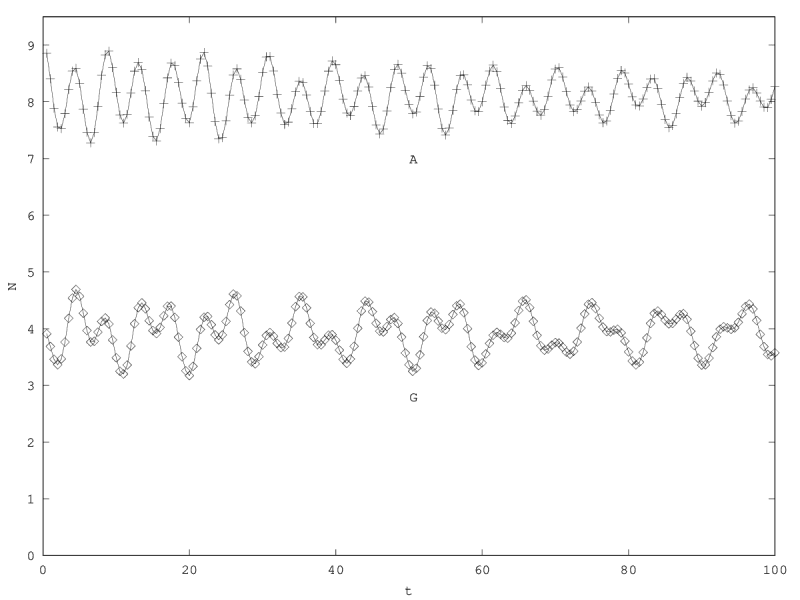
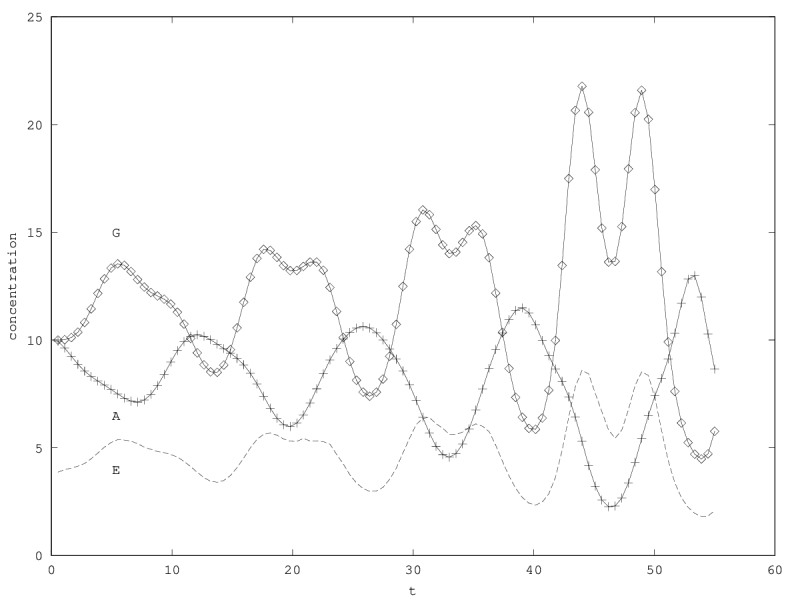
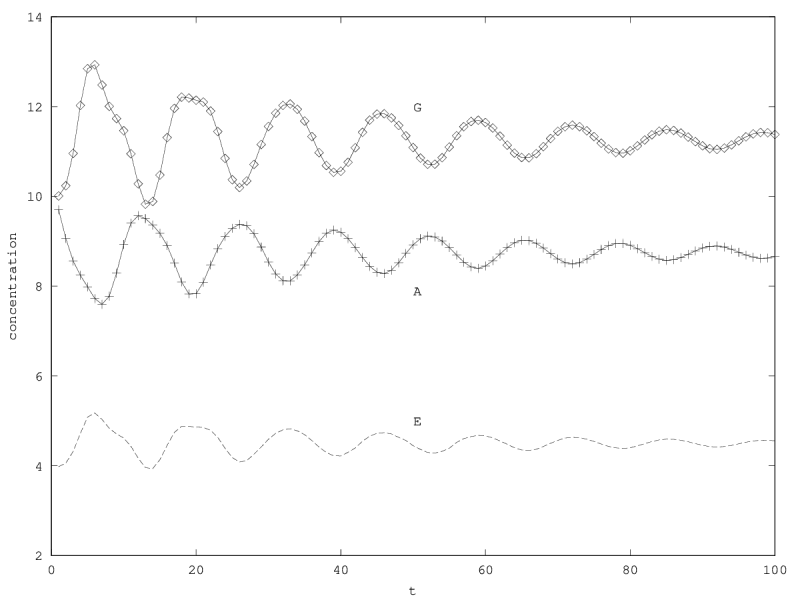
We can investigate the structural stability of the second order model by adding a friction term. (Recall that this term represents also the share of intracellular resources between daughter cells when the limiting factor has non-heritable effects, see our discution on friction in the previous article.)

$$\frac{dr{}_A}{dt}=\frac{a\phi }{A+G}-m-\frac{d}{1+bE}-f{r}_A$$

$$\frac{dr{}_G}{dt}=\frac{a\phi }{A+G}-m-c-f{r}_G$$

The equation for enzyme dynamics is as before:

$$\frac{dE}{dt}=\frac{-1}{{\tau }_E}E+i+eG$$

We will treat this case by numerical experimentation (figure 2, 2, 2). It turns out that friction counteracts the inertia introduced by the enzyme decay rate ( ${\tau }_E$). Starting from a case with amplified oscillations (without friction, figure 2), we first add a relatively low friction term (compared to the parameter $1∕{\tau }_E$ having the same dimension), and damped oscillations obtain (figure 2). Last, when increasing the enzyme characteristic time enzyme ${\tau }_E$, $G$ population crashes, which can be interpreted as an effect of the competitive advantage of $A$ cells taking advantage of the longest presence of the plasmatic enzyme (figure 2). It turns out that $f$ and $1∕{\tau }_E$, conjointly, increase the stability of the coexistence. This might be interpreted as an effect of $f$ opposing to extreme fluctuations that can drive a population to extinction and slowing down the dynamics at the same time, and an effect of $1∕{\tau }_E$ that make $A$ cells more dependent on $G$ cells. In time-scale separation terms, it can be said that coexistence is favored when the enzyme has a fast dynamics ( $1∕{\tau }_E$ important) as regards the population dynamics (slowed down by $f$).

3 Gene therapy model: discussion

This work seeks to investigate the possible perturbations of cell population dynamics with a therapeutic aim. From the therapeutic point of view, such a modeling work can be considered as a mean to optimize the research of relevant empirical variables.

3.1 Therapeutic perspectives

When considering the first order model, it appears that enzyme injection is counterproductive for ADA-SCID gene therapy, in the sense that within a stable coexistence equilibrium, injections do not increase the quantity $E^{\ast }$ of enzyme and decrease the amount $G^{\ast }$ of modified cells. This result is structurally stable. Generally speaking, let us write $𝜃\left(E\right)$ the increase in mortality of non-modified cells due to the lack of enzyme (in our model, $𝜃\left(E\right)=d∕(1+bE)$); we also write $f$ the response function to resources and $h$ the function describing the enzyme dynamics. The following system is:

$$\begin{array}{llll}\hfill \frac{dG}{Gdt}& =f(a\phi ,A+G,m)-c& \hfill & \\ \hfill \frac{dA}{Adt}& =f(a\phi ,A+G,m)-𝜃\left(E\right)& \hfill & \\ \hfill \frac{dE}{dt}& =h(E,{\tau }_E,i,e,G)& \hfill & \end{array}$$

Coexistence at the equilibrium entails that $𝜃\left(E^{\ast }\right)=c$. When the equation $𝜃\left(E\right)=c$ cannot be satisfied whatever the value of $E$, the coexistence is impossible at the equilibrium, and $A$ always win when $𝜃\left(E\right)<c$, $G$ always win when $𝜃\left(E\right)>c$.

The equilibrium is stable when $d𝜃\left(E\right)∕dE<0$. This condition means that for the equilibrium to be stable, the increase in mortality due to lack of enzyme shall decrease when the enzyme quantity increases (this condition is fulfilled in our model).

Under coexistence, $𝜃\left(E^{\ast }\right)$ determines $E^{\ast }$, which does not depend on i. $E^{\ast }$ determines $G^{\ast }$ via the function $h(E,{\tau }_E,i,e,G)$. If $h$ is increasing as a function of $i$ and increasing as a function of $G^{\ast }$ (which seems reasonable), keeping fixed $E^{\ast }$ and all the parameters in $h$ except $i$ and $G^{\ast }$, then:

$$\frac{{dE}^{\ast }}{dt}=0=\frac{\partial h}{\partial i}di+\frac{\partial h}{\partial G^{\ast }}{dG}^{\ast }$$

that is:

$$\frac{{dG}^{\ast }}{di}=\frac{-\frac{\partial h}{\partial i}}{\frac{\partial h}{\partial G^{\ast }}}$$

As $\partial h∕\partial i>0$ and $\partial h∕\partial G^{\ast }>0$ according to our biological hypotheses, it turns out that $d{G}^{\ast }∕di<0$. Thus $G^{\ast }\left(i\right)$ is decreasing, and can eventually become negative. From a biological point of view, this means that above a given injection threshold, engraftment of modified $G$ cells is impossible, and that injections lower the amount of enzyme effectively produced by $G$ cells. These two behaviors were empirically observed by Aiuti et al (2002b).

We would like to draw attention to the fact that this reasoning holds at the equilibrium only (and, also, if there is coexistence, which seems to be the case at the scale of several years). From a therapeutic point of view, it can be unavoidable to resort to sporadic enzyme injections when the patient is in bad condition Aiuti et al (2002b), to temporarily increase the enzymatic level above its equilibrium value. Notice however, that the injections should then take place on a period as short as possible (in approximately one month, the plasmatic enzyme seems to go back to its pre-injection equilibrium value despite the injections, Aiuti et al (2002b) Fig.1). In addition to the observed decrease in $G$ cells, it is possible that the synthesis of the enzyme by $G$ cells is decreased in presence of the enzyme.

3.1.1 Generalization to other gene therapies

In this study, we focused on a permanent gene therapy. However, the perspective of gene therapies also concerns transitory gene therapies. For instance, in case of a bone fracture, it is possible to modify cells in such a way that they produce osteogenic growth factors and thus improve bone welding. This kind of therapy enables a more spatially targeted treatment than the injection of an exogenous protein Baltzer and Lieberman (2004). In this case, the aim is not the invasion of a tissue by $G$ cells, but in contrast their elimination by $A$ cells: the focal transient behavior is the tissue relaxation time. Using a model in the same vein as above, and assuming that the modified $G$ cells do not benefit more from the growth factors they produce than the non-modified $A$ cells, we could write:

$$\begin{array}{llll}\hfill \frac{dA}{Adt}& =f(a\phi ,A+G,m)& \hfill & \\ \hfill \frac{dG}{Gdt}& =f(a\phi ,A+G,m)-c& \hfill & \end{array}$$ It turns out that the relaxation time is of the magnitude of $1∕c$, where $c$ is the cost of growth factor synthesis by the cell.

A similar model could be used for cancer gene therapies using mesenchymal stem cells. These cells have a positive tropism for tumors and their metastases, and can be transformed to deliver oncolytic viruses of therapeutic proteins specifically on tumoral sites, and their persistence in the patient’s organism is not necessarily wanted (see the review by Dwyer et al (2010)).

3.1.2 Demographic inertia and populations fluctuations

To our knowledge, the available data do not enable to conclude with respect to the importance of demographic inertia in the case of intraorganismal cell population dynamics. Demographic inertia, in particular inertia due to maternal effects, has been discussed in ecology (e.g. Ginzburg and Taneyhill (1994), but see Berryman (1995)). We know of no such a discussion in intra-organismal ecology.

In case of demographic inertia, the populations have their own pulsation and can oscillate around the equilibrium, in particular when they experience perturbations. Oscillatory behaviors, and fluctuations in general, are numerous in intraorganismal ecology (e.g. Wagner et al (1996); Perazzo et al (2000). Notably, some hematological disorders (some leukemias and neutropenias in particular) result in oscillatory behaviors of cell population dynamics with periods ranging from ten to hundred days depending on the disease; in this case, the temporal pattern is even part of the clinical description Birgens and Karle (1993); Haurie et al (1999); Hirase et al (2001); Hirayama et al (2003); Xiao et al (2003); Colijn and Mackey (2005).

As for ADA-SCID gene therapy, the lymphocyte number fluctuates (from a factor one to six, see Aiuti et al (2002a)) but the data are insufficient to assess the potential intrinsic period of the population dynamics. Given the state of current knowledge, we thus cannot ascribe oscillatory behaviors to an intrinsic demographic inertia, in contrast with an external forcing. However, the search for oscillatory mechanisms could answer this question, in a potentially easier way than for macro-organisms, thanks to the shorter characteristic time of demographic renewal. Notice however that in intraorganismal ecology, we could expect that the organism exerts a friction on potential oscillations of cell populations to be able to maintain a certain homeostasis. This friction would result from cell relationships with their environment and would be thus difficult to isolate in vitro.

The demographic inertia, if proven, could be of importance for cell population management (that is, in our case, for managing non-modified $A$ and modified $G$ cells populations), first because short time actions can have effects on a longer time scale, second because oscillatory behaviors could lead to destabilization or resonance effects. We have shown that in our case (second order model with injection and enzyme synthesis), the system is not destabilized by enzyme injections, except for extreme values of the parameters. (Notice however that this conclusion holds for relatively frequent injections, as more sporadic injections should be modeled by a Dirac comb, and could still lead to resonance effects with cell population dynamics, possibly to be optimized^[4].)

Generally speaking, even in the absence of external perturbations like enzyme injections, it turns out that demographic inertia can be a source of supplementary instability leading to engraftment failing.

The ecological cell niche can be a source of demographic inertia (in our model, because of the enzyme’s characteristic time ${\tau }_E$), and niche construction can result both in an amplification or, on the contrary, in a damping of oscillations. To have a better grasp on the structural origin of this effect, we can derive once more the equation of the enzyme dynamics. The second order equation is given by:

$$\frac{d^{2}E}{d{t}^2}=-\frac{1}{{\tau }_E}\frac{dE}{dt}+e\frac{dG}{dt}$$

Writing $r_E$ the speed $dE∕dt$ to help identifying structural homologies, we can write the equation of the acceleration $d^{2}E∕d{t}^2$ as:

$$\frac{d^{2}E}{d{t}^2}=-\frac{1}{{\tau }_E}{r}_E+eG{r}_G$$

It appears that $r_E∕{\tau }_E$ behaves as a friction term with respect to the acceleration $d^{2}E∕d{t}^2$. The term $G{r}_G$ represents a non-linearity that explains the complexity of the behaviors described in this paper. Generally speaking, in the linearized system the enzyme dynamics introduces first order terms that are typical of friction and antifriction, while without friction and niche construction the characteristic polynomial is of the form $P\left(X^2\right)$.

As regards the effect of the enzyme on the dynamics, we have chosen a simple model where $G$ cells are not affected by the enzyme concentration (assuming that the intracellular synthesized enzyme concentration is non-limiting), and where the additional mortality (or the additional metabolic cost in the second order model) in $A$ cells is additive to their dynamics. A more general model could consider a non-complete restauration of the cell function by gene therapy and/or where the enzyme effect is not additive with respect to the first order dynamics (that is, the function $f$ would have $E$ as a variable). In this case, $G$ cells dynamics would depend on $E$, but also, $G$ cells could have a priviledged access to the enzyme they themselves synthesize. A simple way to deal with this kind of competitive advantage would be to model the enzyme as being synthesized in an intracellular compartment ( $E_c$, accessible only to $G$ cells), with a transit to an intercellular compartment (here, the blood plasma with a concentration $E$, that would also depend on injections), where it would be both accessible to $A$ and $G$ cells^[5].

4 Conclusion

4.1 Non-equilibrium ecology

In this paper, we investigated the impact of a cell niche construction activity (the synthesis of a missing enzyme) that would not be time-scale separable from the cell population dynamics. This drove us to focus on the importance of transitory dynamics (oscillations, relaxation times) that are due to niche and demographic inertia.

Two different perspectives emerge, given that we consider that ecological interactions should be described as first or second order systems. First order systems describe demographic dynamics that are directly affected by demographic factors (resources, sources of mortality), while second order systems describe demographic dynamics that are indirectly affected, through the interplay at the individual level between metabolism and resource acquisition. At the second order, demographic factors are analoguous to forces in the Newtonian mechanics, that impact the acceleration of a movement and not its speed. In mathematical terms, a supplementary dynamic dimension is added to the definition of the niche.

Ginzburg et al (2004) (p102-103), in a programmatic conclusion, urged ecologists to identify the ecological “forces”, force here having to be understood as a cause inducing a modification of the energetic state of the individuals or of the corresponding growth rate. Among such forces, Ginzbug & Colyvan see energetics, maternal effects, and predator-prey relationships. The niche as a substrate for demographic inertia, and niche construction as an ecological force, could be added to this program.

4.2 From enrichment by ecology to ecology enrichment

In this paper, we have chosen to describe the lymphocyte population with the minimal model of an unstructured population. However, the populations of interest (lymphocyte strains) are, from an ecological point of view, metapopulations that are structured in source-sink populations because of cell differentiation, which might also be correlated to cell age (e.g., hematopoietic stem cell → lymphoid progenitor → lymphoblast → prolymphocyte → lymphocyte → T-lymphocyte, to mention just one strain). The fact that differentiated cells can de-differentiate could be modelled in a structurally homologous way than migration occuring from a sink population in ecology.

Most probably, such a highly structured cell fate, contrained by the cellular environment posed by the organism, should have major dynamical effects. Then “the organism [would be] an ecosystem, but [would be] more than an ecosystem”^[6], and intra-organismal ecology would have to be not just an application, but also a true extension of classical ecology.

Acknowledgements This work is based on notes written up by Regis Ferrière in 2004 after a project started at the CEMRACS 2004, whose participants were Antonio Cappucio, Etienne Couturier, Michel de Lara, Regis Ferrière, Olivier Sester, Pierre Sonigo, Christian et Carlo. The authors also whish to thank the organizers and participants of the StabEco workshop, held at the Laboratory Ecology and Evolution, University of Paris 6, on the 17/12/2010. Philippe Huneman and Minus van Baalen provided invaluable comments on earlier versions of the manuscript.

This work consists in a partial update of a previous work in French (Pocheville 2010:chap.3), realized while both authors were benefiting from a funding from the Frontiers in Life Sciences PhD Program and from the Liliane Bettencourt Doctoral Program. A.P is currently benefiting from a Postdoctoral Fellowship from the Center for Philosophy of Science, University of Pittsburgh. M.M. is currently benefiting from a Postdoctoral Fellowship from the Region Ile-de-France, DIM-ISC.

References

1. Aiuti A (2002) Advances in gene therapy for ada-deficient scid. Current opinion in molecular therapeutics 4(5):515–522
2. Aiuti A, Slavin S, Aker M, Ficara F, Deola S, Mortellaro A, Morecki S, Andolfi G, Tabucchi A, Carlucci F, Marinello E, Cattaneo F, Vai S, Servida P, Miniero R, Roncarolo MG, Bordignon C (2002a) Correction of ada-scid by stem cell gene therapy combined with nonmyeloablative conditioning. Science 296(5577):2410–2413, doi: 10.1126/science.1070104, URL http://www.sciencemag.org/content/296/5577/2410.abstract, http://www.sciencemag.org/content/296/5577/2410.full.pdf
3. Aiuti A, Vai S, Mortellaro A, Casorati G, Ficara F, Andolfi G, Ferrari G, Tabucchi A, Carlucci F, Ochs HD, et al (2002b) Immune reconstitution in ada-scid after pbl gene therapy and discontinuation of enzyme replacement. Nature medicine 8(5):423–425
4. Aiuti A, Cassani B, Andolfi G, Mirolo M, Biasco L, Recchia A, Urbinati F, Valacca C, Scaramuzza S, Aker M, et al (2007) Multilineage hematopoietic reconstitution without clonal selection in ada-scid patients treated with stem cell gene therapy. Journal of Clinical investigation 117(8):2233–2240
5. Aiuti F, Giovannetti A (2003) Structured interruptions of therapy: looking for the best protocol. Aids 17(15):2257–2258
6. Baltzer A, Lieberman J (2004) Regional gene therapy to enhance bone repair. Gene therapy 11(4):344–350
7. Berryman AA (1995) Population cycles: a critique of the maternal and allometric hypotheses. Journal of Animal Ecology pp 290–293
8. Birgens HS, Karle H (1993) Reversible adult-onset cyclic haematopoiesis with a cycle length of 100 days. British journal of haematology 83(2):181–186
9. Cappell B, Aiuti A (2010) Gene therapy for adenosine deaminase deficiency. Immunology and Allergy Clinics of North America 30:249
10. Cassani B, Montini E, Maruggi G, Ambrosi A, Mirolo M, Selleri S, Biral E, Frugnoli I, Hernandez-Trujillo V, Di Serio C, et al (2009) Integration of retroviral vectors induces minor changes in the transcriptional activity of t cells from ada-scid patients treated with gene therapy. Blood 114(17):3546–3556
11. Cavazzana-Calvo M, Thrasher A, Mavilio F (2004) The future of gene therapy. Nature 427(6977):779–781
12. Cavazzana-Calvo M, Lagresle C, Hacein-Bey-Abina S, Fischer A (2005) Gene therapy for severe combined immunodeficiency. Annu Rev Med 56:585–602
13. Colijn C, Mackey MC (2005) A mathematical model of hematopoiesis—i. periodic chronic myelogenous leukemia. Journal of Theoretical Biology 237(2):117–132
14. Dwyer RM, Khan S, Barry FP, O’Brien T, Kerin MJ (2010) Advances in mesenchymal stem cell-mediated gene therapy for cancer. Stem Cell Res Ther 1(3):25
15. Gaspar HB, Aiuti A, Porta F, Candotti F, Hershfield MS, Notarangelo LD (2009) How i treat ada deficiency. Blood 114(17):3524–3532
16. Ginzburg LR, Taneyhill DE (1994) Population cycles of forest lepidoptera: a maternal effect hypothesis. Journal of Animal Ecology 63(1):79–92
17. Ginzburg LR, Colyvan M, et al (2004) Ecological orbits: how planets move and populations grow. Oxford University Press New York
18. Haurie C, Dale DC, Mackey MC (1999) Occurrence of periodic oscillations in the differential blood counts of congenital, idiopathic, and cyclical neutropenic patients before and during treatment with g-csf. Experimental hematology 27(3):401–409
19. Hirase N, Abe Y, Muta K, Ishikura H, Umemura T, Nawata H, Nishimura J (2001) Autoimmune neutropenia with cyclic oscillation of neutrophil count after steroid administration. International journal of hematology 73(3):346–350
20. Hirayama Y, Sakamaki S, Tsuji Y, Matsunaga T, Niitsu Y (2003) Cyclic platelet and leukocyte count oscillation in chronic myelocytic leukemia regulated by the negative feedback of transforming growth factor $\beta$. International journal of hematology 77(1):71–74
21. Lehmann L (2008) The adaptive dynamics of niche constructing traits in spatially subdivided populations: evolving posthumous extended phenotypes. Evolution 62(3):549–566
22. Marangoni F, Bosticardo M, Charrier S, Draghici E, Locci M, Scaramuzza S, Panaroni C, Ponzoni M, Sanvito F, Doglioni C, et al (2009) Evidence for long-term efficacy and safety of gene therapy for wiskott–aldrich syndrome in preclinical models. Molecular Therapy 17(6):1073–1082
23. Netti PA, Baxter LT, Boucher Y, Skalak R, Jain RK (1995) Time-dependent behavior of interstitial fluid pressure in solid tumors: implications for drug delivery. Cancer Research 55(22):5451–5458
24. Perazzo C, Fernandez E, Chialvo D, Willshaw P (2000) Large scale-invariant fluctuations in normal blood cell counts: A sign of criticality? Fractals 8(3):279–283, doi: 10.1142/S0218348X00000329, URL http://www.worldscinet.com/fractals/08/0803/S0218348X00000329.html
25. Sangalli M, Maroni A, Zema L, Busetti C, Giordano F, Gazzaniga A (2001) In vitro and in vivo evaluation of an oral system for time and/or site-specific drug delivery. Journal of controlled release 73(1):103–110
26. Sauer AV, Aiuti A (2009) New insights into the pathogenesis of adenosine deaminase-severe combined immunodeficiency and progress in gene therapy. Current opinion in allergy and clinical immunology 9(6):496–502
27. Wagner C, Nafz B, Persson P (1996) Chaos in blood pressure control. Cardiovascular research 31(3):380–387
28. Xiao Z, Hao Y, Qin T, Han Z (2003) Periodic oscillation of blood leukocytes, platelets, and hemoglobin in a patient with chronic eosinophilic leukemia. Leukemia research 27(1):89–91

5 Appendices

5.1 Linearized first order model, with two species and niche construction (enzyme synthesis)

After linearization, we seek for the eigenvalues of the system (of dimension 3). These eigenvalues are roots of the characteristic polynomial:

$$X^3+X^2\left(M+\frac{1}{{\tau }_E}\right)+X\frac{M}{{\tau }_E}+Be\frac{c^{2}b}{d}$$

where $M=m+c$ and:

$$B=M\frac{2}{a\phi }\left(\frac{a\phi }{M}-G^{\ast }\right)$$

It turns out that in the case where there is coexistence, two scenarii are possible:

1. The polynomial has three negative roots: in this case the system converges exponentially toward equilibrium
2. or the polynomial has a negative root and two conjugated complex solutions. In this case the system is stable or unstable according to the sign of the real part of the roots. In the case where the system is stable, the regime is pseudoperiodical with damped oscillations.

The literal resolution of the polynomial can be easily realized, but the literal expression of the solutions is too complicated to be informative.

5.2 Linearized second order system with two species, enzyme construction, and time-scale separation on the enzyme dynamics

The following characteristic polynomial obtains:

$$X^2+MX+Bc\frac{2}{d}$$

where $M=m+c$ and:

$$B=M\frac{2}{a\phi }\left(\frac{a\phi }{M}-G^{\ast }\right)$$

and :

$$G^{\ast }=\frac{1}{be{\tau }_E}\left(\frac{d}{c}-1-bi{\tau }_E\right)$$

The polynomial discriminant is $\Delta$:

$$\Delta =M^2-4Bc\frac{2}{d}$$

Thus

$$\Delta =M^2\left(1-4c\frac{2}{da\phi }\left(\frac{a\phi }{M}-G^{\ast }\right)\right)$$

If $\Delta >0$, then:

$$X=\frac{-M\pm \sqrt{\Delta }}{2}$$

If there is coexistence then we have $a\phi ∕M-G^{\ast }>0$, then these two roots are negative and the system has oscillations near the equilibrium.

If $\Delta <0$, then :

$X=\frac{-M\pm j\sqrt{\Delta }}{2}$; where $j^2=-1$.

In this case the eigenvectors have a dynamics in a $\exp \left(Zt\right)$ form, where $Z^2=X$. However, the real part of the roots is negative, thus for each root one of the $Z$ has a positive real part and the equilibrium is unstable. The system diverges with amplified oscillations.

When the quantity $i$ of the injections increases, $G^{\ast }$ decreases thus $\Delta$ decreases. Increasing $i$ makes the instability closer. If $1<4c^2∕\left(dM\right)$, then increasing $i$ destabilizes the system. We then ignore which one of the two populations $A$ and $G$ will survive, which in particular depends on the initial conditions.