Biological organisation as closure of constraints
Journal of Theoretical Biology
We characterize biological organization as a closure of constraints, where constraints are defined at a given time scale and are interdependent.
Abstract
We propose a conceptual and formal characterisation of biological organisation as a closure of constraints. We first establish a distinction between two causal regimes at work in biological systems: processes, which refer to the whole set of changes occurring in non-equilibrium open thermodynamic conditions; and constraints, those entities which, while acting upon the processes, exhibit some form of conservation (symmetry) at the relevant time scales. We then argue that, in biological systems, constraints realise closure, i.e. mutual dependence such that they both depend on and contribute to maintaining each other. With this characterisation in hand, we discuss how organisational closure can provide an operational tool for marking the boundaries between interacting biological systems. We conclude by focusing on the original conception of the relationship between stability and variation which emerges from this framework.
Keywords: Biological organisation, Closure, Constraints, Symmetries, Time scales
Table of contents
Reading time: ~88 min
Biological organisation as closure of constraints
Abstract
We propose a conceptual and formal characterisation of biological organisation as a closure of constraints. We first establish a distinction between two causal regimes at work in biological systems: processes, which refer to the whole set of changes occurring in non-equilibrium open thermodynamic conditions; and constraints, those entities which, while acting upon the processes, exhibit some form of conservation (symmetry) at the relevant time scales. We then argue that, in biological systems, constraints realise closure, i.e. mutual dependence such that they both depend on and contribute to maintaining each other. With this characterisation in hand, we discuss how organisational closure can provide an operational tool for marking the boundaries between interacting biological systems. We conclude by focusing on the original conception of the relationship between stability and variation which emerges from this framework.
1 Introduction
In Theoretical Biology, an enduring tradition has placed heavy emphasis on the idea that biological systems realise what could be referred to as “self-determination”. That is, in very general terms, the capacity of a system’s constitutive organisation to contribute to the determination and maintenance of its own conditions of existence through the effects of its activity (see also Mossio & Bich ( 2014), for more details). Usually (Weber & Varela, 2002), the origin of this tradition is traced back to the characterisation of biological systems as “self-organising”, as Kant proposed in his Critique of Judgement (Kant, 1790). Over the last two centuries a number of authors, more or less explicitly inspired by Kant, have been proposing conceptual and theoretical accounts aimed at understanding the principles underlying biological self-determination.
Following Claude Bernard’s seminal work (Bernard, 1865, 1878), during the first half of the 20th century self-determination was initially investigated as homeostasis (Cannon, 1929) and mathematically expressed in terms of feedback loops by first-order Cybernetics (Wiener, 1948; Ashby et al., 1956). Homeostasis, however, is a general systemic capacity, exhibited by both biological organisms and some artefacts (as the classical example of the thermostat shows). Accordingly, recent contributions have aimed at going beyond the limitations of the notion of homeostasis in order to better capture the specificities of biological self-determination. In this respect, relevant contributions were made during the 1960s by embryology ( Weiss, 1968). Waddington, in particular, suggested that in the biological domain homeostasis should be interpreted as homeorhesis (stability of dynamics rather than stability of states), insofar as in biological systems what “is being held constant is not a single parameter but is a time-extended course of change, that is to say, a trajectory” (Waddington, 1968, p.12).
A crucial step in the theoretical elaboration of biological self-determination is the account put forward by Piaget (Piaget, 1967), whose core idea is to integrate in a single coherent picture two inherent dimensions of biological systems: thermodynamic openness and organisational closure. On the one hand, biological systems are, as von Bertalanffy ( von Bertalanffy, 1952) had already emphasised, thermodynamically open (dissipative) systems, traversed by a continuous flow of matter and energy; yet on the other, they realise closure, which refers to mutual dependence between a set of constituents which could not exist in isolation, and which maintain each other through their interactions. In Piaget’s view, biological self-determination is specifically related to closure which, through the association between division of labour and mutual dependence that it implies, captures a fundamental aspect of the idea of “organisation” as such. In a word, biological systems self-determine because they are organised, and they are organised because they realise closure.
The centrality of organisational closure and its connection to organisation, as well as its distinction from (and complementarity to) thermodynamic openness, have become givens in most subsequent accounts of biological self-determination (Letelier et al., 2011). One of the best known formulations is the one centred on the concept of autopoiesis ( Varela et al., 1974; Varela, 1979) which, among other aspects, emphasises on the generative dimension of closure: biological systems self-determine in the specific sense that they “make themselves” (auto-poiein). Precisely because of their dissipative nature, the components of biological systems are maintained only insofar as they maintain and stabilise not just some internal states or trajectories, but the autopoietic system itself , as an organised unity[1].
In spite of its qualities, however, the concept of autopoiesis (and related computational models, see McMullin (2004)) suffers in our view from a central weakness, insofar as it does not provide a sufficiently explicit characterisation of closure. Biological systems are at the same time both thermodynamically open and organisationally closed, but no details are given regarding how the two dimensions are interrelated, how closure is actually realised, what constituents are involved, and at what level of description. In the absence of such specifications, as already highlighted by previous critical interpretations of the autopoietic theory (see in particular Fleischaker (1988); Ruiz-Mirazo & Moreno (2004)), it remains unclear in what precise sense closure would constitute a causal regime which distinctively characterises biological organisation and its capacity for self-determination. In particular, closure might be generically understood as a causal regime involving some sort of circularity, fundamentally no different from the numerous examples of circular chains of transformations, that frequently occur in the natural (although not necessarily biological) world. Is there some principled difference between biological closure and all other kinds of causal cycles ?
A concerted attempt to answer this question has been made by Robert Rosen, who has explicitly claimed that a sound understanding of biological organisation should account for the distinction between closure and openness in terms of a distinction between two causal regimes. In Life Itself (Rosen, 1991), Rosen’s account of closure is based on a reinterpretation of the Aristotelian categories of causality and, in particular, on the distinction between efficient cause and material cause. Let us consider an abstract mapping
An analysis of Rosen’s account in all its richness would by far exceed the scope and limits of this paper. Let us just mention that, recently, several studies have made substantial contributions to re-examining, interpreting and developing Rosen’s ideas (Piedrafita et al., 2010; Letelier et al., 2003, 2006; Wolkenhauer & Hofmeyr, 2007). What matters for our present purposes is that closure, and therefore self-determination, is located at the level of efficient causes: what constitutes the organisation is the set of efficient causes subject to closure, and its maintenance (and stability) is the maintenance of the closed network of efficient causes.
In this paper, we develop an account of organisational closure which is directly inspired by and, we believe, consistent with the theoretical framework established by Rosen. Nevertheless, although Rosen made clear progress in the understanding of biological organisation with respect to previous formulations, we believe that his characterisation of closure is not fully satisfactory. The main limitation is that it remains too abstract, and therefore hardly applicable as a guiding principle for biological theorising, modelling and experimentation. Closure is defined by Rosen as involving efficient causes but, without additional specifications, it might be difficult to identify efficient causes in the system: what entities actually play the role of efficient causes in a biological system? How should the relevant level of causation at which self-determination occurs be characterised?
To deal with this issue, decisive insights have emerged from more recent literature which emphasise, in line with Piaget’s initial view, the “thermodynamic grounding” of biological systems ( Bickhard, 2000; Christensen & Hooker, 2000; Moreno & Ruiz-Mirazo, 1999). In particular, Stuart Kauffman (Kauffman, 2002) suggests retrieving the classic idea of “work cycle” (in the sense of the Carnot engine), and applying it within the context of self-maintaining biochemical reactions. Based on Atkins’s ideas about work, conceived as a “constrained release of energy” (Atkins, 1984), Kauffman argues that a circular relationship between work and constraints must be established in a system in order to achieve self-determination, in the form of a “work-constraint (W-C) cycle”. When a (W-C) cycle is realised, constraints which apply to the system are not independently given (as in the Carnot engine) but rather are produced and maintained by the system itself. Hence, the system needs to use the work generated by the constraints in order to generate those very constraints, by establishing a mutual relationship, i.e. a cycle, between constraints and work.
In a fundamental sense, the account of closure that we provide in this paper lies at the intersection between Rosen’s and Kauffman’s proposals. In particular, our central thesis is that organisational closure should be understood as closure of constraints, a regime of causation which is at the same time distinct from - and related to - the underlying causal regime of thermodynamic openness. It is important to underline that our purpose is by no means to provide a model of closure which would adequately capture the complexity of real biological systems. Rather, we conceive this paper as a contribution to characterise in precise terms some of the general features of closure, which might subsequently be used to develop models of biological organisation. Our aim, in other words, is to explicitly state what makes closure a distinctive causal regime, characteristically at work in biological systems[2].
The structure of the paper is as follows. In section 2, we specify the main idea which underpins our characterisation of closure. In particular, we put forward an understanding of biological self-determination in terms of spatio-temporally localised constraints exerted on physical and chemical processes. In section 3, we develop specific theoretical and formal criteria for drawing a distinction between constraints and processes, which correspond to two regimes of causation. Section 4 goes one step further, by elucidating how the idea of dependence among constraints should be conceived in the biological domain. Section 5 introduces closure, as the specific case of mutualdependence between a set of constraints. Section 6 provides a preliminary account of how closure can be used to draw boundaries between interacting biological systems. Finally, in the conclusion, we briefly discuss how the present framework conceives the relations between invariance and variation, between stability and change in biological phenomena.
2 Biological determination as self-constraint
The main aim of this paper is to understand organisational closure in terms of the mutual dependence which exists among a set of entities that fulfil the role of constraints within a system.
What do we mean by constraints? In contrast to fundamental physical equations and their underlying symmetries, constraints are contingent causes[3], exerted by specific structures or dynamics, which reduce the degrees of freedom of the system on which they act. As additional causes, they simplify (or change) the description of the system, and enable an adequate explanation of its behaviour to be provided, an explanation which might otherwise be under-determined or wrongly determined.
In describing physical and chemical systems, constraints are usually introduced as external determinations (boundary conditions, parameters, restrictions on the configuration space, etc.), which contribute to determining the behaviour and dynamics of a system, although their existence does not depend on the dynamics on which they act (Pattee, 1972, 1973). To take a simple example, an inclined plane acts as a constraint on the dynamics of an object sliding or rolling on it, whereas the constrained dynamics (the sliding) do not play a causal role in producing and/or maintaining the plane itself. In some cases, however, the constrained dynamics do play a role in determining the conditions of existence of (a subset of) the constraints acting on them; in some specific circumstances, in particular, the existence of each constraint depends on the existence of the others, as well as on the action that they exert on the dynamics. In this kind of situation, the set of constraints realises self-determination as organisational closure.
The idea behind this conception of closure is that biological self-determination occurs in the form of self-constraint. Like all open systems, be they physical or chemical, biological systems are traversed by a flow of energy and matter, which takes the form of processes and reactions occurring in open thermodynamic conditions. In this respect, organisms do not differ, qualitatively, from other natural thermodynamically open systems. At the same time, however, one of the specificities of biological systems is the fact that the thermodynamic flow is constrained and canalised by a set of constitutive constraints in such a way as to establish a specific form of mutual dependence between those very constraints. Accordingly, the organisation of the constraints can be said to achieve self-determination as self-constraint, since the conditions of existence of the constitutive constraints are, because of closure, mutually determined within the organisation itself[4].
In this paper, we base the theoretical and formal characterisation of closure on the concept of symmetry (see for example Weyl ( 1983); Goodman & Wallach (2009)). In very general terms, symmetries refer to transformations that do not change the relevant aspects of an object: symmetries and invariants (of energy, momentum, electrical charges, etc.) are therefore complementary concepts, both mathematically and physically. In describing an object, symmetries are relevant in relation to different aspects, which might not be spatial in the intuitive sense. For example, the notion that two replicates of an experiment correspond to the same kind of situation relies on an assumption of symmetry between their respective behaviours. Another example comes from classical electromagnetism, in which the transformation that inverts all charges (changing positive charges to negative ones and vice versa) does not alter the resulting behaviour, and can therefore be understood as a symmetry of the equations involved. In mathematical approaches to natural phenomena, symmetries justify the theories formulated (Van Fraassen, 1989; Bailly & Longo, 2011; Longo & Montévil, 2014). In particular, symmetries are at the core of the constitution of scientific objects: they ground their theoretical and mathematical characterisation (by defining their description space) and make it possible to write equations describing their behaviour (i.e. their specific trajectory) in those situations in which the values of the parameters and initial conditions are specified[5].
The theoretical characterisation of closure as a specific kind of symmetry provides, we submit, a principle for understanding the stabilisation of biological phenomena. One of the authors of this paper has recently argued (Longo & Montévil, 2011, 2014) that biological systems can be understood in terms of “extended critical transitions”, which mean that they form coherent structures, whose proper[6] symmetries are inherently unstable. Biological symmetries may change unpredictably, both at the individual and evolutionary scale. In contrast to the role played by theoretical symmetries in the mathematical and theoretical definition of physical objects, their instability in the biological domain underlies the fundamental contextuality, variability and historical nature of biological phenomena. In the light of these background assumptions, it follows that theoretical symmetries in biology are contingent and can have only a limited temporal range of applicability.
The theoretical framework developed in this paper aims to complement this picture by exploring how biological symmetries can display some degree of stabilisation at the relevant temporal and spatial scales. Constraints correspond to theoretical symmetries that are local, in the sense of being stable at limited temporal and spatial scales. These symmetries are related to specific dynamics and structures which constitute biological systems, and which are usually investigated (theoretically and experimentally) by biological science. For its part, organisational closure refers to the encompassing causal regime through which constitutive constraints achieve further stabilisation. Given that, ex hypothesi, biological symmetries are unstable, biological systems achieve self-determination insofar as organisational closure involves their stabilisation in the long run. As such, closure is at the core of the very constitution of biological phenomena as scientific objects.
We will come back to the relations between stability and variation in our framework in the conclusion section. Now, let us develop the notion of constraints in more explicit conceptual and formal terms.
3 Constraints and processes
The characterisation of closure relies on a theoretical distinction between two different regimes of causation, which we propose to ground in terms of a distinction between processes and constraints (exerted on the processes).
In a general sense, processes refer to the whole set of changes (typically physical processes, chemical reactions, etc.) that occur in biological systems and involve the alteration, consumption, production and/or constitution of relevant entities. Constraints, on the other hand, refer to entities which, while acting upon these processes, can be said from the appropriate viewpoint to remain unaffected by them. A given theoretical entity, as we will see, cannot be qualified as a constraint per se, but only in relation to a specific process and the relevant time scale at which this process occurs. This context- and scale-dependence is, in our view, a general feature of constraints. In this section, we suggest defining constraints as entities which exhibit a symmetry with respect to a process (or a set of processes) that they help stabilise. More formally:
Definition 1 (Constraint) Given a process
- I/
- The situations
Note
- II/
- A temporal symmetry is associated with all aspects of
Conditions I and II can be met after (properly justified) quantitative approximations[7]. The situation which fulfils conditions I-II will be expressed as
Let us now discuss each of these conditions, and the motivation behind them. We will refer to two concrete examples: the action of the vascular system on the flow of oxygen, and that of an enzyme on a chemical reaction.
- I/
- The first condition requires that a constraint exerts a causal role on the target process. In formal terms, we express this by stating that the situations with or without the constraint are different[8] (asymmetric). This must be true when considering the effects of the constraint rather than its mere presence[9].
Consider the vascular system. There is an asymmetry between the flow of oxygen when considered under the influence of the vascular system (
Similarly, there is an asymmetry between a chemical reaction when considered under the influence of an enzyme (
- II/
- A constraint, while it changes the way in which a process behaves, is not altered by (i.e. is conserved through) that process at the scale at which the latter takes place. The second condition captures this property by stating that
Again, let us consider the examples. A temporal symmetry is associated with the vascular system
Similarly, a temporal symmetry is associated with the configuration of an enzyme, which is conserved during the reaction[11]. Note that at time scales shorter than
Since they meet the two conditions, both the vascular system (with respect to oxygen transport) and enzymes (with respect to the catalysed reaction) can be considered constraints within the organism.
It is of fundamental importance to emphasise that each condition is met only at the relevant time scale and, in particular, that the time scale
The key role of time scales in the definition of constraints should not obscure the fact that the specific definition of a constraint uses other aspects also, such as the spatial scale. Indeed, in order to adequately characterise processes, and the constraints acting on them, one must consider the relevant system, and hence the relevant quantity of space (extension, volume, etc.). For example, it is necessary to consider a system large enough to include the flow of oxygen and the topology of the vascular system (thus, it must be a system of at least the same size than the vascular system itself). However, while it is of course true that constraints do depend on spatial scales, we maintain that this scale does not play a specific role in characterising constraints in the sense that, on a first approximation[13], variations in the spatial scale do not affect the symmetries which define them. In contrast, constraints are altered when the temporal scale varies. The proper symmetries of biological constraints can be broken over time and, therefore, must be actively maintained or rebuilt within the system (which, as we will see, leads to organisational closure). Moreover, as mentioned in the Introduction, constraints may be reorganised in unpredictable ways over time (Longo et al., 2012a).
A similar point holds true for the levels of description, which can be roughly thought of as the degree of “detail” or “granularity” with which a situation is described at some temporal and spatial scales. In many cases, an equivalence can be drawn between the descriptions of constraints at different levels. For instance, the vascular system can be described as a smooth surface forming a tube (its topology) or as a collection of cells clustered together in a specific way (with the same “tube” topology). Some levels of description may be more suitable than others for explanatory reasons; and yet, the proper symmetries of the constraints do not vary — again, on a first approximation[14] — when different levels of description are considered. Accordingly, levels of description do not play a specific role in the characterisation of constraints and are therefore not included in the definition.
Because of their capacity to exert a causal influence on the thermodynamic flow without being influenced by that flow, constraints have, from a thermodynamic perspective, very special features. A description of the causal role of constraints in terms of thermodynamic exchanges may possibly be relevant to understanding the intermediate steps leading to the effect (such as the sequence of alterations of an enzyme during catalysis), but would be irrelevant to understanding the overall effect, which does not involve a flow between the constraint (or more precisely, its relevant aspects as mentioned in the definition) and the constrained process or reaction.
Before moving on, let us first discuss two significant theoretical and epistemological issues, both related to the characterisation of the causal role of constraints.
The first one concerns the fact that, following our definition, a constraint alters the behaviour of a process although, strictly speaking, it does not lead in many cases to new possible behaviours for the constrained process[15]. More technically, when the set of possibilities are determined by conserved quantities, the latter cannot be altered by fluxes coming from constraints, which are themselves, by definition, conserved through (i.e. are symmetric with regard to) the process. For instance, a constraint does not play a role in the balance equation of a given chemical reaction, an equation which is based on the conservation of matter (i.e. the conservation of the quantity of every type of atom and electron). That chemical reaction would therefore be possible in principle, but so slow (or, from a molecular viewpoint, so unlikely) that it would require centuries to take place, and would be quantitatively irrelevant. The causal role of constraints (here, like enzymes) is to accelerate the reaction enough to actually achieve the result at a shorter (and biologically relevant) time scale.
By claiming that, in many cases, constraints do not generate new possibilities for the constrained processes, the above remark explicitly suggests that constraints are mostly limiting, insofar as they canalise (condition I) the constrained processes toward a specific outcome from among a set of already possible ones. At first glance, this characterisation seems to diverge from related analyses of the role of constraints in explaining biological organisation. In particular, as Juarrero (1999) has pointed out, the constraints at work in biological systems are generative, in the sense that they enable behaviours and outcomes that would otherwise be impossible. Is there a theoretical disagreement here? We believe the distinction between limiting and generative constraints corresponds to a difference in the time scale at which their causal effects are described. We maintain that the constrained dynamics or outcomes could in most biological cases occur in an unconstrained way at the relevant (very long, or infinite) time scale; yet, at biological (shorter) time scales, constraints are indeed required in order to actually achieve these specific dynamics and outcomes because they contribute to producing otherwise improbable (or virtually impossible) effects. In particular, each constitutive constraint within a biological organism enables the maintenance of other constrains as well as, because of closure, the whole system. As a result, although constraints are mostly limiting at longer time scales, they can be pertinently conceived as generative at shorter time scales: in this sense, this characterisation is perfectly consistent with our account that claims that biological organisation could not exist without the causal action of constraints.
The second issue is related to our understanding of the causal role of constraints stemming from the conjunction of conditions I and II. Condition II stipulates that, at
Even in those cases in which functional constraints, prima facie, appear (see footnote 16 above) to transmit energy, we hold that they do in fact channel an energy transfer while being conserved. Consider the example of the heart which, according to the usual description, “pumps the blood”: is this a case of a macroscopic constraint which contravenes our definition because it transmits kinetic energy to the blood? In our view, such a conclusion stems from an incorrect description of the constraints involved. To see why, let us decompose the situation in which “the heart gives kinetic energy to the blood”. Under the initial conditions, blood is located at some point in the body and energy is stored, in a chemical form, in the cardiomyocytes. After pumping (our target process), blood circulation is accelerated and the cardiomyocytes have produced chemical waste. This rough decomposition shows that “the heart”, understood as a region of space inside the organism, in fact includes entities (both the blood’s hydrodynamic state and the cardiomyocytes) which, in our framework, should be considered processes. What then are the relevant constraints? In this situation, the constraints are the elements of the complex multiscale structure of the heart that channel the transfer of the cardiomyocytes’ chemical energy to the blood’s kinetic energy. These elements include (among others) the relevant components of the cardiac cells (mitochondria, sarcomeres, myofibrils), which transform chemical energy into mechanical forces, the geometric architecture of the heart and its electric conduction structure that macroscopically shapes these forces both spatially and temporally. All these entities remain approximately (see note 7 above) conserved after a heart beat, while constraining the release of chemical energy. In short, we could refer to it as the “architecture” of the heart at this time scale, and claim that such an architecture constrains the transformation of the chemical energy (
The central outcome of the theoretical distinction between constraints and processes is a distinction between two regimes of causation. For a given effect of a process or reaction, one can theoretically distinguish, at the relevant time scale, between two causes: the inputs or reactants (in Rosen’s terms, the “material” causes) that are altered and consumed through the process, and the constraints (the “efficient” causes, at
4 Dependence
Organisational closure occurs in the specific case of mutual dependence between (at least some of) the constraints acting on a biological system. Before discussing closure as such, let us first focus on the relationship of dependence between constraints.
In the previous section, constraints are defined as entities which, at specific time scales, are conserved (symmetric) with respect to the process, and are therefore not the locus of a transfer. However, constraints are typically subject to degradation at longer time scales, and must be replaced or repaired. When the replacement or repair of a constraint depends (also) on the action of another constraint, a relationship of dependence is established between the two.
Let us consider a constrained process
This situation establishes a dependence between constraints in which constraint
Definition 2 (Dependence between constraints) Following the above line of reasoning, we define a relationship of dependence between constraints as a situation in which, given two time scales
-
- There is an object
In this situation, we say that
By way of example, let us consider the production of an enzyme. As discussed above, an enzyme acts as a constraint on the reaction it catalyses. In turn, enzymes are themselves produced by and within the cell, through the translation process: ribosomes build the primary sequence of the future protein on the basis of the messenger rna (m rna) sequence, without consuming it. Since the ribosomes and the m rna play a causal role while being conserved during this process, they both act as constraints (at a specific time scale) on the production of the enzyme. Consequently, the relationship between the enzyme, the ribosomes and the m rna can be pertinently described as a dependence between constraints (in which the enzyme depends on both ribosomes and mrna), insofar as all of these entities satisfy the definition of constraint at specific time scales, which are considered jointly.
Let us examine some relevant implications of the above definition.
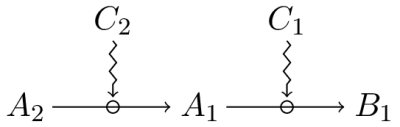
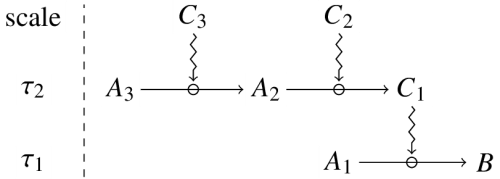
Firstly, a dependence between constraints is conceptually different from dependence between processes, which corresponds to a situation in which a set of constraints act successively on a chain of processes depending on each other[17]. In the following diagram, for instance:
process
Secondly, a relationship of dependence between constraints does not involve a thermodynamic flow between the generative and the dependent constraints. Indeed, because of condition II, the conservation of
In a general sense, dependence between constraints can be taken as the organisational principle underlying any “repair mechanisms” at work in the organism which, in addition to the wide-ranging literature on dna repair (Friedberg et al., 1995), also include the repair of all kinds of parts of an organism (Wang et al., 2009; Bergamini, 2006)[19]. Repair requires the existence of a part (
Thirdly (and this is important for preventing possible misconceptions in the next section), dependence between constraints can occur in two different ways, depending on the relations between the time scales involved: slow dependence with
In the first case
Slow and fast dependence differ in an interesting way. When the dependent constraint is faster, its stability is quite straightforward because something that changes very slowly seems to stand still from the point of view of something faster. In the opposite case, when the dependent constraint is slower (which is actually the case for many chemicals involved in development), then a sustained and stable activity of the faster process is required. As we will suggest in the following section, organisational closure necessarily requires the joint realisation of both kinds of dependence.
The last step of this section introduces the notion of direct dependence between constraints.
Definition 3 (Direct dependence between constraints)
-
- There is at least one relevant aspect of
As we will see in the following section, we argue that the notion of direct dependence plays a fundamental role in organisational closure. Although we do not provide in this paper a theoretical justification for this claim, the importance of direct dependence is related to the degree of functional integration and complexity realised by biological systems: the very existence of the dynamic organisation requires that the maintenance of each constraint subject to closure be under the direct, close control of some other constraints subject to closure. An indirect, and therefore looser, dependence would presumably be incompatible with the requirements for such a high degree of complexity and coordination.
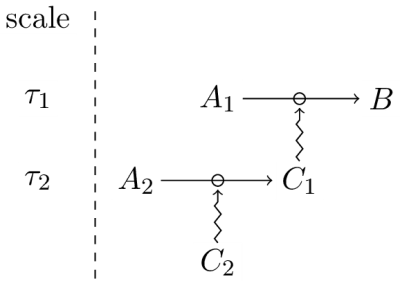
In the above example,
Consider again the example of enzyme formation. The maturation of the protein can be successively constrained by different entities; the catalysis performed by the enzyme depends directly only on the constraint exerted on the last process involved. The relevant aspect impacted in this case is the conformation of the protein or, more precisely, its ability to react to the relevant chemicals, and the last process involved is the action of other proteins on the endoplasmic reticulum, in eukaryotic cells. Accordingly, the mrna population discussed above is only an indirect generative constraint with respect to the conformation of the protein produced; in turn, it directly contributes to determining the number of proteins produced during the translation process discussed above, which is a different aspect of the dependent constraint.
5 Closure
Let us now turn to closure, which we interpret as a specific property of a system with respect to dependence between constraints.
Definition 4 (Closure) A set of constraints
-
- There is at least one other constraint
A set
-
Overall closure refers then to an organisation in which each constraint is involved in at least two distinct dependence relationships; in other words, each constraint plays the role of both generative and dependent constraint. The condition added for strict closure is aimed at ensuring that the definition applies only to one system (rather than two independent systems). In what follows we will use the generic term ’closure’ to refer to strict closure unless specified otherwise. The network of all those constraints that meet the three requirements of closure is, we hold, collectively able to self-determine through self-constraint. Note also that the second condition does not require direct dependence. The reason is that, while each constraint of
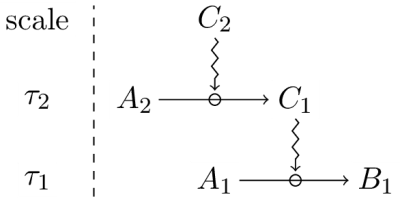
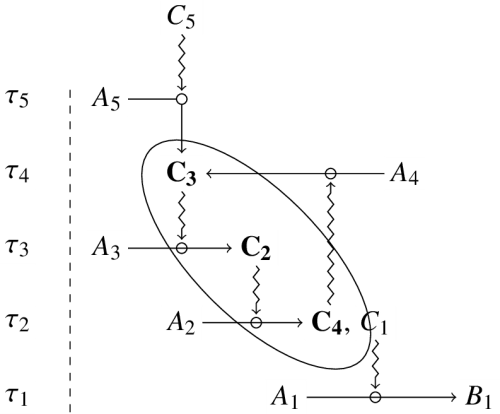
As an illustration of closure, consider the following network of dependent constraints:
In this diagram,
It should be noted that two scales must be considered for every constraint (
As mentioned in the introduction, this characterisation of closure is, of course, very general and schematic, and unable to capture the complexity of its actual realisations by biological systems. Yet at the same time it is precise enough to derive several implications.
Firstly, as argued recently (Mossio et al., 2009; Saborido et al., 2011) and mentioned briefly in section 3 above, we claim that constraints subject to closure constitute biological functions. Within this framework, performing a function is equivalent to exerting a constraining action on an underlying process or reaction. All kinds of biological structures and traits to which functions can be ascribed satisfy the definition of constraint given above, albeit at various different temporal and spatial scales. In addition to the vascular system and enzymes mentioned above, some intuitive examples include, at different scales, membrane pumps and channels (which constrain both the inward and outward flow of materials through the membrane) and organs (such as the heart which constrains the transformation of chemical energy into blood movement). Closure is then what grounds functionality within biological systems: constraints do not exert functions when taken in isolation, but only insofar as they are subject to a closed organisation.
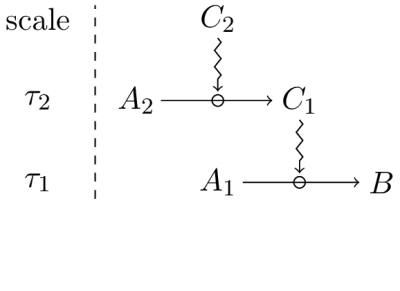
Secondly, closure should be clearly distinguished from independence, insofar as a system which realises closure is a physically open system, inherently coupled to the environment with which it exchanges energy and matter (Nicolis & Prigogine, 1977). This implies in particular that closure is a context-dependent determination, to the extent that it is always realised with respect to a set of specific boundary conditions, which includes several external (and independent) constraints acting on the system (such as, for instance, constraint
Thirdly, closure of constraints is different from the underlying open regime of thermodynamic processes since, as discussed in section 3, constraints are conserved through the thermodynamic flow at the relevant time scales. Hence, a description of closure in terms of the causal regime of thermodynamic changes would be inadequate, since it would be unable to include constraints as such and their contribution as causal factors. In particular, a description of biological organisation which does not use the causal power of constraints and their closure would amount to a system constituted by a cluster of unconnected processes and reactions, whose coordinated occurrence would be theoretically possible at very long time scales (see the discussion in section 3), but extremely unlikely (virtually impossible) at biologically relevant time scales[23].
To conclude this section, let us discuss in a very preliminary way how closure can be described in practice. As a matter of fact, although closure is different from the thermodynamic flow, it does unfold over time, mainly because the various functional constraints do not usually operate simultaneously. Moreover, as mentioned, constraints are such at different time scales, which means that closure is a multiscale causal regime. Jointly considered, these features raise the question of how a description of the closed network of dependencies can be obtained. At least two aspects should be mentioned here.
Firstly, a sufficiently long duration has to be considered, in order to include all the relevant time scales (from shorter to longer) at which each constitutive constraint can be described, providing the dynamics of the biological system continue to take place. Usually, for example, the description of an adult mammal organism requires the consideration of those constraints exerted on relevant processes with the time scales ranging between a fraction of a second (for fast neural or mechanical phenomena) and a substantial fraction of the organism’s lifespan (for slow phenomena which are nevertheless fast enough to be sustained by and within the organisation, such as the maintenance of bone structure)[24].
Secondly, once the constraints have been included, the organisation of dependencies between them must be described. This can only be done by abstracting them from the physical time in which they occur, since closure cannot be described at a given point in time, but rather requires us to consider a set of processes taking place at different time scales (some processes may not be permanent, but rather may occur cyclically as is the case with heartbeats, for example). Thus, the whole network of dependencies should be considered as one “block” extended over multiple time scales. Accordingly, closure consists of an interdependent relational network of dependencies, extracted from the dynamics of the system in physical time.
With this general characterisation in mind, we deal in the next section with the application of closure as a theoretical criterion for drawing boundaries between systems in the biological domain.
6 Closure and boundaries
In principle, closure constitutes a clear-cut criterion for drawing the boundary between a biological entity and its environment. In organisational terms, in fact, the set of constraints subject to closure define the system, whereas all other constraints (and specifically those which have causal interactions with the system), belong to the environment. Accordingly, the ascription of closure to a system calls for a “yes or no” answer, usually based on a topological (circular) property of the network of interactions (whatever the underlying mathematical framework). At first glance, this holds true for our characterisation: in our abstract example above, constraints
Nevertheless, one may wonder whether (and indeed how), without further specifications, closure can be ascribed to parts of organisms on the one hand, and to systems whose constituents are themselves organisms on the other. In other words, the question of the “lower and upper” boundaries of closure calls for a conceptual and formal treatment; in this section, we take some preliminary steps in this direction.
Let us consider first the lower boundaries of closure ascription. The crucial remark is that, in practice, any actual description of closure in biological systems is a partial one, as a complete characterisation of the whole set of mutually dependent constraints is usually not available, and constitutes a sort of “theoretical horizon” of biological explanation.
Consequently, the incompleteness of current descriptions may generate a dilemma: either closure is to be ascribed to whatever system fit these incomplete descriptions, in which case some parts of biological systems may possibly be taken as closed; or closure is to be ascribed only to those systems for which complete descriptions are currently available, in which case virtually no system would meet the requirements.
In order to overcome this difficulty, we suggest the following strategy. In the absence of complete descriptions, closure should only be ascribed to maximally closed systems, i.e. those systems which include all mutually dependent constraints, in the available description. Maximally closed systems therefore constitute the lowest boundary of closure ascription: in principle, no subsystem of collectively dependent constraints that can be shown to belong to an encompassing closed system can be said to realise closure[26].
Let us now turn to all those cases in which two or more biological organisms establish a form of mutual dependence due to stable interactions between them, such that each of them can be said to rely on the other(s) for its own maintenance. In these situations, in which a fundamental organisational continuity exists between the interacting organisms, the upper boundaries of closure ascription seem to extend beyond each organism, insofar as the notion of maximally closed system applies only to the encompassing system which contains all (known) constraints subject to closure. If we were to limit ourselves to this analysis, it would be impossible to describe systems including different nested levels of organisational closure and systems belonging to closed systems (and specifically mutually dependent organisms) would not themselves realise closure as discussed above. Moreover, since biological organisms are systematically involved in such interactions it would follow that most of the time individual organisms cannot be said to realise closure. The main theoretical upshot would be a serious weakness for any account based on closure, which could not be considered a distinctive property of organisms in many biologically relevant cases. In the remainder of this section, we will address this challenge in a (preliminary) conceptual and formal way. We distinguish three different situations in which two or more closed systems realise mutual dependence.
The first situation is that in which the disjunction between the interacting closed systems is straightforward. In this case, either there is no mutual dependence between the two closed systems or, if there is a mutual dependence, then the relationship between the systems is, at least in one direction, one of indirect dependence. To use the technical terms introduced in section 5 above, the encompassing system which includes the interacting systems realises overall closure, but not strict closure. For instance, consider the case of a group of humans in which there is a division of labour, with some members being in charge of hunting, and others in charge of cooking. Let us suppose that both hunting and cooking could be pertinently characterised as macroscopic constraints exerted on the flow of energy and matter. Collectively, there is some mutual dependence between the members of the group, although the dependence on hunting would presumably be indirect, in the precise sense that the processes constrained by hunting are followed by other processes that contribute to the maintenance of the organisation of the members of the group. Of course, a finer-grained description of this kind of dependence would be needed, but we will leave that for a future paper. For the purposes of this paper, we simply suppose that many cases of biological interactions could be pertinently described in terms of indirect mutual dependence; thus, the characterisation of closure we provided, which explicitly requires direct dependence (so as to capture a distinctive feature of biological integration), makes it possible to exclude these kinds of looser, although mutually beneficial, interactions.
The two other situations that we discuss in the following sub-sections both involve, ex hypothesi, direct mutual dependence between organisms. Firstly, there are cases in which a limited number of individual organisms realise mutual dependence, a situation which results in the establishment of an encompassing closed system (such as for instance in the classical example of mutualistic symbiosis). As we will suggest, organisational boundaries can be drawn in this case between the interacting organisms, although they do not correspond to strict discontinuities but rather to a quantitative evaluation of the tendency to closure (section 6.1). Secondly, we will examine those cases of populations or groups of organisms which collectively contribute to the emergence of an encompassing closure; cells in multicellular organisms are a paradigmatic example. In this kind of situation, we argue (in section 6.2) that the closure of the collective system may, in some conditions, be separated from that realised by the constitutive organisms. Such separation provides the grounds for characterising different levels of closure.
6.1 Tendency to closure
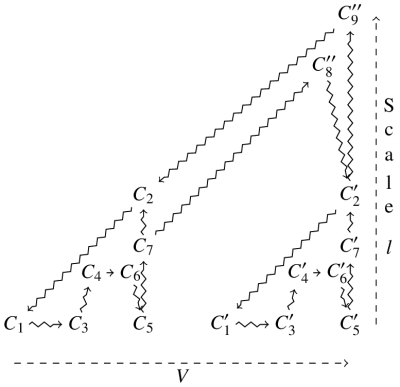
Let us consider two or more biological organisms (two abstract cells), each of which could be said to realise closure when taken in isolation. Moreover, let us assume that the cells establish strong interactions resulting in direct mutual dependence. As a result, the encompassing system is the maximally closed system which realises closure. In this situation, is there a legitimate way to argue that the individual interacting cells also realise closure? As mentioned above, closure is usually considered a Boolean property. Here, we propose to apply our characterisation in a different way, and to describe a procedure which enables closed systems to be delimited through the drawing of their spatial boundaries. The general idea is to use a quantitative assessment of the tendency of constraints to be “packed together” in space.
Let us choose an arbitrary volume of space
A procedure to represent the boundaries between the interacting cells can be implemented by relying on this measure of complexity. Let us presuppose some a priori knowledge of the localisation of the considered cells in space, which guides the choice of the initial volume[29]. Any increase of
We submit that the
The tendency to closure is a measure of the degree of organisational integration of organisms and, as well as, an operational tool for drawing the boundaries between them, even when they establish functional dependence. It is worth emphasising, in this respect, that such a measure comes in degrees. For example, one can conjecture that the tendency to closure is higher for a unicellular eukaryote than for a cell in a metazoan. Similarly, the tendency to closure of a biofilm is arguably weaker than that of an individual bacterium, or a metazoan. The same differences might also emerge when comparing closed systems located at various nested levels of organisation (see the following subsection), such as, for instance, in the case of the ant and its colony.
Although the above treatment is still preliminary, the formal expression of the tendency to closure (as a quantitative assessment of organised complexity) will hopefully pave the way to future scientific exploration.
6.2 Hierarchical boundaries of closure
The tendency to closure makes it possible to identify relevant biological interacting entities in those (widespread) cases in which there is some degree of functional overlap between them. In this sub-section, we discuss a different kind of situation, in which a closed organisation is composed of constituents which themselves realise closure: the paradigmatic example is a multicellular organism made up of its cellular constituents.
One possible view on this situation is that the cells contribute to the realisation of the multicellular organism and are, therefore, also subject to the encompassing closure. Consequently, the boundaries of each individual cell can only be drawn by measuring their tendency to closure, as discussed in the previous section.
However, we submit that this situation has specific properties. Indeed, individual cells usually do not technically exert a constraint which contributes to the maintenance of the multicellular system. Rather, functions subject to multicellular closure are exerted by populations or groups of cells that form tissues and organs. In the formal framework proposed in the previous section, this situation can be described by emphasising two aspects, both related to the very definition of constraint. Firstly, the contribution of an individual cell does not meet condition I of the definition of constraint, for the specific reason that its effects on the process are negligible. For example, the contribution of an individual epithelial cell to the regulation of insulin levels is negligible. Secondly, individual cells also fail to meet condition II, insofar as the relevant symmetries which characterise the constraint are respected at higher scales (both spatial and/or temporal) than those at which the individual cells are described. For example, in relation to the constraint exerted on the blood flow by blood vessels, it is fairly apparent that many cells are required to obtain the geometrical and topological properties on the basis of which the relevant constraint becomes operational.
Thus, overall, it seems that cells do not usually act as constraints individually, but only collectively, when they are assembled in tissues and organs. Consequently, it follows that in most cases there is no mutual dependence between each cell and the encompassing system, enabling their respective closures to be separated, even though they realise a nested hierarchy (the closure of the cells is nested within the closure of the encompassing system). In a sense, this implies that the internal functional aspects of the cells can be separated from those aspects that matter for the organism’s organisation. The separation between nested closures provides a straightforward basis for drawing the boundaries between organisms[30].
We conjecture that a relationship between two closures of constraints which involves both separation and a nested hierarchy provides the theoretical basis for characterising, in our framework, a distinction between levels of organisation. Two closed regimes constitute two different levels of organisation if they are both separated and hierarchically nested; accordingly, cells and multicellular organisms constitute two different levels of organisation.
We leave a full-fledged analysis of this issue for future work. Let us simply mention that other levels of organisation could presumably be identified beyond the unicellular and multicellular ones: an example could be ecosystems ( Nunes-Neto et al., 2014). At the same time, not just any level of description would qualify as a level of organisation in this technical sense: arguably, a relatively small number of levels could be identified in the biological realm.
7 Conclusion: invariance and variation
In this paper, we have argued that the specificity of biological systems lies in their capacity for self-determination as self-constraint. As discussed above, the central idea is that self-constraint occurs in biological systems in the form of closure, i.e. a causal regime in which a set of mutually dependent constraints act on the flows of energy and matter so as to collectively maintain themselves, and their organisation, over time. In turn, the fundamental formal distinction between the two regimes of causation at work (constraints and processes) relies on the identification of symmetries, and local conservations, at the relevant (temporal) scales.
As a conclusion, we would like to examine an underlying theoretical implication of this framework, already evoked in section 2, i.e. the fact that closure constitutes a principle of stabilisation of biological organisation and, therefore, a fundamental biological invariant. At the same time, the invariance of closure by no means signifies that biological systems are not subject to variability. Let us develop this idea.
As argued above, closure takes place in a temporal interval, and can be described by abstracting the network of closed dependencies from the time flow. In this formal framework, the claim according to which closure constitutes an “invariant” of biological organisation technically means that a description of closure is possible for any interval long enough to describe a sufficient set of constraints and their mutual dependencies. In other words, given a minimum duration, closure is realised for any interval of equivalent duration chosen in the system’s lifetime. The stabilisation of biological phenomena results specifically from the continuous control exerted over processes and reactions by functional constraints whose maintenance in the long run depends in turn on their mutual dependence through closure. The invariance of closure grounds the stabilisation of the functional organisation.
Stabilisation, however, does not prevent variation, which may refer to two different kinds of changes. On the one hand, organised constraints can exhibit negligible variations, i.e. variations which do not affect their functional role and do not, therefore, alter the overall organisation. This may be the case when the variation occurs only at short time scales (and is then compensated for), or when then variation is irrelevant with regards to the effects of the constraint on the process. On the other hand, biological systems may (and do) undergo functional changes both throughout their lifespan and over the generations. These changes affect the structure and function of one or more constraints, which in turn result in a modification of the organisation. Functional variations are related to many factors, including the life cycle and the interactions with the environment, as well as random changes.
In some cases, functional variation threaten the viability of the whole system, and may possibly lead to its break-up[31]. The crucial thing to bear in mind in this respect, however, is that functional variation is not merely an obstacle for the maintenance of the biological organisation; rather, it is also a crucial requirement for the adaptivity, increase in complexity and ultimately the long-term sustainability of life (Ruiz-Mirazo et al., 2004). Indeed, in addition to their functional role within a specific organised system, constraints also play a role in enabling the emergence of new constraints, new organisations and new behaviours, typically at the evolutionary and populational scales ( Longo et al., 2012a; Longo & Montévil, 2013). Reciprocally, functional variation alters the organisation and yet must be subject to closure in order to be sustained over time. The contingency of biological systems, and their capacity to undergo changes for both intrinsic and extrinsic reasons, justifies the need for the collective maintenance of the constraints.
As biological systems undergo functional variations, their organisation maintains closure, albeit realised in different variants, because of the continuous acquisition of some functions, and the loss of others. In this sense, the invariance of closure takes place at a level of description which is higher than that at which each specific organisation (instantiated by an individual system) occurs. Understood in this way, the invariance of closure may be said to be complementary to its functional variation, with both being constitutive principles for biology. In a word, the role of closure as a principle of stabilisation becomes all the more important when the contingency of biological systems is placed at the heart of their understanding.
Acknowledgements
We would like to warmly thank Cliff Hooker, Giuseppe Longo, Kepa Ruiz-Mirazo (special mention) and John Stewart for their careful reading and useful remarks on previous versions of this paper. Maël Montévil held a postdoctoral fellowship from the Région Île-de-France, DIM “Problématiques transversales aux Systèmes Complexes”.
References
- Ashby, W. R. et al. (1956). An introduction to cybernetics volume 2. Chapman & Hall London.
- Atkins, P. W. (1984). The second law. New York: freeman.
- Bailly, F., & Longo, G. (2011). Mathematics and the natural sciences; The Physical Singularity of Life. London: Imperial College Press. Preliminary version in French: Hermann, Vision des sciences, 2006.
- Bergamini, E. (2006). Autophagy: A cell repair mechanism that retards ageing and age-associated diseases and can be intensified pharmacologically. Molecular Aspects of Medicine, 27, 403 – 410. doi: 10.1016/j.mam.2006.08. 001 .
- Bernard, C. (1865). Introduction à l’étude de la médecine expé rimentale. Paris: Baillière.
- Bernard, C. (1878). Leçons sur les phénoménes de la vie communs aux animaux et aux végétaux.
- von Bertalanffy, L. (1952). Problems of Life: An Evaluation of Modern Biological Thought.. New York: John Wiley & Sons.
- Bickhard, M. H. (2000). Autonomy, function, and representation. Communication and Cognition-Artificial Intelligence, 17, 111–131.
- Cannon, W. B. (1929). Organization for physiological homeostasis. Physiological reviews, 9.
- Christensen, W., & Hooker, C. (2000). Autonomy and the emergence of intelligence: Organised interactive construction. Communication and Cognition-Artificial Intelligence, 17, 133–157.
- Fleischaker, G. R. (1988). Autopoiesis: the status of its system logic. Biosystems, 22, 37 – 49. doi: 10.1016/0303-2647(88)90048-2 .
- Friedberg, E. C., Walker, G. C., Siede, W. et al. (1995). DNA repair and mutagenesis.. Washington DC: American Society for Microbiology (ASM) Press.
- Goodman, R., & Wallach, N. (2009). Symmetry, representations, and invariants. Dordrecht: Springer Verlag.
- Juarrero, A. (1999). Dynamics in Action: Intentional Behavior as a complex System.. Cambridge: MIT Press.
- Kant, I. (1790). Critique of judgment. English translation: Pluhar, W. S., 1987. Hackett Publishing. Indianapolis.
- Kauffman, S. (2002). Investigations. Oxford University Press, USA.
- Letelier, J.-C., Cárdenas, M. L., & Cornish-Bowden, A. (2011). From l’homme machine to metabolic closure: Steps towards understanding life. Journal of Theoretical Biology, 286, 100 – 113. doi: 10.1016/j.jtbi.2011. 06.033 .
- Letelier, J. C., Marin, G., & Mpodozis, J. (2003). Autopoietic and (m,r) systems. Journal of Theoretical Biology, 222, 261 – 272. doi: 10.1016/ S0022-5193(03)00034-1 .
- Letelier, J.-C., Soto-Andrade, J., Abarzúa, F. G., Cornish-Bowden, A., & Cárdenas, M. L. (2006). Organizational invariance and metabolic closure: Analysis in terms of systems. Journal of Theoretical Biology, 238, 949 – 961. doi: 10.1016/j.jtbi.2005.07.007 .
- Longo, G., & Montévil, M. (2011). From physics to biology by extending criticality and symmetry breakings. Progress in Biophysics and Molecular Biology, 106, 340 – 347. doi: 10.1016/j.pbiomolbio.2011.03.005 .
- Longo, G., & Montévil, M. (2013). Extended criticality, phase spaces and enablement in biology. Chaos, Solitons & Fractals, 55, 64 – 79. doi: 10.1016/j.chaos.2013.03.008 .
- Longo, G., & Montévil, M. (2014). Perspectives on Organisms: Biological time, symmetries and singularities. Lecture Notes in Morphogenesis. Dordrecht: Springer. doi: 10.1007/978-3-642-35938-5 .
- Longo, G., Montévil, M., & Kauffman, S. (2012a). No entailing laws, but enablement in the evolution of the biosphere. In Genetic and Evolutionary Computation Conference. GECCO’12 New York, NY, USA: ACM. doi: 10.1145/2330784.2330946 .
- Longo, G., Montévil, M., & Pocheville, A. (2012b). From bottom-up approaches to levels of organization and extended critical transitions. Frontiers in Physiology, 3. doi: 10.3389/fphys.2012.00232 . Invited paper.
- McMullin, B. (2004). Thirty years of computational autopoiesis: A review. Artificial life, 10, 277–295.
- Miquel, P.-A. (2014). Aging as alteration. In R. L., & F. T. (Eds.), Aging Facts and Theories. Karger volume 39 of Interdiscipl Top Gerontol. Basel. doi: 10.1159/000358906 .
- Moreno, A., & Mossio, M. (2015). Biological autonomy. A Philosophical and Theoretical Enquiry.. Dordrecht: Springer.
- Moreno, A., & Ruiz-Mirazo, K. (1999). Metabolism and the problem of its universalization. Biosystems, 49, 45 – 61. doi: 10.1016/S0303-2647(98) 00034-3 .
- Mossio, M., & Bich, L. (2014). La circularité biologique: concepts et modèles. In F. Varenne, M. Silberstein, P. Huneman, & S. Dutreuil (Eds.), Modéliser & simuler. Episté mologies et pratiques de la modélisation et de la simulation (pp. 137–170). Editions Matériologiques volume 2.
- Mossio, M., Bich, L., & Moreno, A. (2013). Emergence, closure and inter-level causation in biological systems. Erkenntnis, 78, 153–178.
- Mossio, M., Saborido, C., & Moreno, A. (2009). An organizational account of biological functions. The British Journal for the Philosophy of Science, 60, 813–841. doi: 10.1093/bjps/axp036 .
- Nicolis, G., & Prigogine, I. (1977). Self-organization in non-equilibrium systems. New York: Wiley.
- Nunes-Neto, N., Moreno, A., & El Hani, C. (2014). Function in ecology: an organizational approach. Biology & Philosophy, 29, 123–141.
- Pattee, H. (1972). The nature of hierarchical controls in living matter volume 1. Academic Press: New York.
- Pattee, H. (1973). Hierarchy theory. New York: Braziller.
- Piaget, J. (1967). Biologie et connaissance; essai sur les relations entre les regulations organiques et les processus cognitifs,.
- Piedrafita, G., Montero, F., Morán, F., Cárdenas, M. L., & Cornish-Bowden, A. (2010). A simple self-maintaining metabolic system: Robustness, autocatalysis, bistability. PLoS Comput Biol, 6, e1000872. doi: 10.1371/journal.pcbi.1000872 .
- Rosen, R. (1991). Life itself: a comprehensive inquiry into the nature, origin, and fabrication of life. Columbia U. P.
- Ruiz-Mirazo, K., & Moreno, A. (2004). Basic autonomy as a fundamental step in the synthesis of life. Artif. Life, 10, 235–259. doi: 10.1162/1064546041255584 .
- Ruiz-Mirazo, K., Peretó, J., & Moreno, A. (2004). A universal definition of life: Autonomy and open-ended evolution. Origins of life and evolution of the biosphere, 34, 323–346. doi: 10.1023/B:ORIG.0000016440.53346.dc .
- Saborido, C., Mossio, M., & Moreno, A. (2011). Biological organization and cross-generation functions. The British Journal for the Philosophy of Science, 62, 583–606. doi: 10.1093/bjps/axq034 .
- Van Fraassen, B. (1989). Laws and symmetry. Oxford University Press, USA.
- Varela, F. (1979). Principles of biological autonomy. North Holland New York.
- Varela, F., Maturana, H., & Uribe, R. (1974). Autopoiesis: The organization of living systems, its characterization and a model. Biosystems, 5, 187 – 196. doi: 10.1016/0303-2647(74)90031-8 .
- Waddington, C. H. (1968). The basic ideas of biology. In C. H. Waddington (Ed.), Towards a theoretical biology: Prolegomena (pp. 1–41). New York: Atheneum.
- Wang, J., Michelitsch, T., Wunderlin, A., & Mahadeva, R. (2009). Aging as a consequence of misrepair–a novel theory of aging. Arxiv preprint arXiv:0904.0575,.
- Weber, A., & Varela, F. (2002). Life after kant: Natural purposes and the autopoietic foundations of biological individuality. Phenomenology and the Cognitive Sciences, 1, 97–125. doi: 10.1023/A:1020368120174 .
- Weiss, P. A. (1968). Dynamics of development: experiments and inferences. New York Academic Press.
- Weyl, H. (1983). Symmetry. Princeton: Princeton University Press.
- Wiener, N. (1948). Cybernetics. Cambridge: MIT Press.
- Wolkenhauer, O., & Hofmeyr, J.-H. S. (2007). An abstract cell model that describes the self-organization of cell function in living systems. Journal of Theoretical Biology, 246, 461 – 476. doi: 10.1016/j.jtbi.2007.01.005 .