Theoretical principles for biology: variation
Progress in Biophysics and Molecular Biology
Biological variation should be given the status of a fundamental theoretical principle in biology. Variation goes with randomness, historicity and contextuality.
Abstract
Abstract Darwin introduced the concept that random variation generates new living forms. In this paper, we elaborate on Darwin’s notion of random variation to propose that biological variation should be given the status of a fundamental theoretical principle in biology. We state that biological objects such as organisms are specific objects. Specific objects are special in that they are qualitatively different from each other. They can undergo unpredictable qualitative changes, some of which are not defined before they happen. We express the principle of variation in terms of symmetry changes, where symmetries underlie the theoretical determination of the object. We contrast the biological situation with the physical situation, where objects are generic (that is, different objects can be assumed to be identical) and evolve in well-defined state spaces. We derive several implications of the principle of variation, in particular, biological objects show randomness, historicity and contextuality. We elaborate on the articulation between this principle and the two other principles proposed in this special issue: the principle of default state and the principle of organization.
Keywords: Variability, Historicity, Genericity, Biological randomness, Organization, Theory of organisms
Table of contents
Reading time: ~98 min
- 1 Introduction
- 2 Invariance and symmetries: physics as the domain of generic objects
- 3 Variation and symmetry changes: biology as the domain of specific objects
- 4 Bringing organization into the picture
- 5 Non-identical iteration of morphogenetic processes
- 6 Conclusions: back to theoretical principles
- Acknowledgments
- References
- Footnotes
Theoretical principles for biology: Variation
Abstract
Darwin introduced the concept that random variation generates new living forms. In this paper, we elaborate on Darwin's notion of random variation to propose that biological variation should be given the status of a fundamental theoretical principle in biology. We state that biological objects such as organisms are specific objects. Specific objects are special in that they are qualitatively different from each other. They can undergo unpredictable qualitative changes, some of which are not defined before they happen. We express the principle of variation in terms of symmetry changes, where symmetries underlie the theoretical determination of the object. We contrast the biological situation with the physical situation, where objects are generic (that is, different objects can be assumed to be identical) and evolve in well-defined state spaces. We derive several implications of the principle of variation, in particular, biological objects show randomness, historicity and contextuality. We elaborate on the articulation between this principle and the two other principles proposed in this special issue: the principle of default state and the principle of organization.
Keywords: Variability, Historicity, Genericity, Biological randomness, Organization, Theory of organisms
Tsung-Dao Lee
L. Pasteur
1 Introduction
A striking feature of living beings is their ability to change. All naturalists know that two individuals of the same species usually display important qualitative differences. All experimentalists know that two replicate experiments can give quite unexpectedly different results – even in the absence of any abnormality in the experimental setup.
Variation took a central role in biological reasoning in Darwin’s book The Origin of the Species (1859) in which it served as a means to explain the current diversity of life, by virtue of the concept of “descent with modification” (Darwin 1859, 119–24): organisms might show some differences from their parents, these differences might be heritable and, under some proper conditions, accumulate to form new lineages. Importantly, to Darwin, some of these variations would be “chance” variations, that is, changes that would be unrelated to the conditions of existence of the organisms, and even unpredictable (Darwin 1859 p.p 131, 314)[1]. In so doing, Darwin introduced contingency and historicity into biological thinking: accidents would happen along life’s trajectory, which would at the same time be unpredictable, unrepeatable, and have long lasting effects (Gould 2002, 1334).
In this paper, we elaborate on the Darwinian idea of “chance” variation. We argue that variation should be given the status of a principle in biology, and in particular organismal biology. Informally, the principle of variation states that biological objects (such as organisms) continually undergo modifications. Some of these variations have functional repercussions, which we discuss with precise concepts in section 3). Moreover, whatever the mathematical frame used to describe an object, unpredictable variations are nevertheless possible: the principle of variation thus implies that the existence of exceptions is the rule in biology. However, a proper biological theory cannot be a mere catalog of exceptions. Accommodating the changes biological organisms undergo during their lives (ontogenesis), as well as during evolution (phylogenesis), in a general theory is a specific challenge raised by biological systems, in particular in contrast to physical theorizing.
In physics, theoretical definitions enable us to discuss abstractly and adequately the behavior of objects (such as the trajectory in space of a punctual object of mass m in classical mechanics, or the behavior of quantum objects as a vector in a Hilbert space in Quantum Mechanics). Such a theoretical framework does not (yet) exist for the biology of organisms and our proposal aims at contributing to the elaboration of the “biological counterpart” of the theoretical frameworks and abstract objects at work in physics.
It is worth emphasizing that, although we will elaborate on the concept of variation by analogy with and in contrast to the physico-mathematical perspective, we by no means advocate a physico-mathematical treatment of biological phenomena. Rather, we think that biology in general, and the biology of organisms in particular, requires a significant change of perspective with respect to the physical viewpoints and methodologies. Typically, physics provide an ahistorical understanding of the phenomena studied[2]. In contrast to physics and in line with the theory of evolution, we argue that historicity is an essential feature of biological phenomena and that biological historicity stem from the principle of variation.
The principle of variation is related to the other principles put forward in this special issue: the biological default state (proliferation with variation and motility), and the principle of organization. The default state is described as a primary generator of variation; when a cell divides, it generates two non-identical cells (Ana Soto et al. 2016). The principle of variation specifies the nature of the difference between these cells. The principle of organization is a way to interpret biological functions as a property stemming from the role that parts play in the maintaining of a system (Mossio, Montévil, and Longo 2016; Mossio, Saborido, and Moreno 2009; Montévil and Mossio 2015). According to this principle, a biologically relevant part (constraint) both depends on and maintains other parts of the organism, thus forming a mutual dependence (labeled “closure” for historical reasons). In (Mossio, Montévil, and Longo 2016), variation and organization are discussed as two intertwined principles: organization is a condition for variation and favors its propagation, whereas variation is a condition for the maintenance and adaptation of biological organization and for the generation of functional innovations. In section 4 of this text, we argue that any relevant variation is a variation of an organization.
Biological variation occurs at all levels of organization, from the molecular level to large scale structures and functions (West-Eberhard 2003; Dueck, Eberwine, and Kim 2016). Single cell observations on one side and high throughput technologies on the other enable biologists to observe both inter-cellular and inter-individual variations, which have received an increasing amount of attention (Elowitz et al. 2002; Collective 2005; Rivenbark, O’Connor, and Coleman 2013). There are many generators of variation among which are random gene expression, instability in morphogenetic processes and randomness in biological rhythms. In particular, cellular proliferation generates variation (Ana Soto et al. 2016). As for temporal scales, living systems undergo variation during their lives (ontogenesis), as well as during evolution (phylogenesis), and these two aspects cannot be analyzed independently (Danchin and Pocheville 2014). In this paper, we focus on variation as a general feature of biological systems without a privileged level of analysis. This enables us to discuss general features that are proper to biology and to stress key differences with respect to physics.
The central implication of this paper is the distinction between the objects as conceived in physical theories (generic objects) and the objects as conceived in biology on the basis of biological variation (specific objects)[3]. In what follows, we discuss first shortly what generic objects are, what kind of manipulation they enable, and how their analysis grounds physical theories (section 2). Then, we contrast generic objects with the variation that biological objects exhibit. We propose that biological objects should be understood as specific (in section 3). Specific objects are, in particular, fundamentally historical, variable and contextual. Thus, the specificity of organisms encompasses biological individuation and diversity. We also discuss the interplay between specific objects and physical morphogenesis. Then, in section 4 we elaborate on the integration between the principle of variation and the principle of organization, between the notion of biological specificity for biological objects and the notion of organization and “contingent genericity" (Moreno and Mossio 2015; Montévil and Mossio 2015; Mossio, Montévil, and Longo 2016). Finally, we develop the idea that biological systems are characterized by the non-identical iterations of morphogenetic processes (section 5).
2 Invariance and symmetries: physics as the domain of generic objects
The principle of variation poses novel challenges with respect to how mathematics enables us to describe the world. To better identify these challenges, we first make a detour by physics and show the role mathematics play in physical theories.
Physics is based on mathematized theories. Historically, the development of physical theories has been intertwined with the development of appropriate mathematics to frame and define their objects: they have “co-evolved”.
We submit that mathematized physical theories rely on the manipulation of generic objects (Bailly and Longo 2011; Longo and Montévil 2014a). The notion of generic objects is abstract, as it lies at the core of physicomathematical reasoning. However, the intuitive idea is quite simple: generic objects are objects which are all of the same kind from the point of view of the theory (they typically obey the same equations). An apple, the Earth, an anvil, for example, are all objects with a given mass and center of gravity and, from the point of view of classical mechanics, they all obey the same equations in the vacuum. Moreover, they continue to obey the same equation during their dynamics even though they undergo some changes: this is because, in physical language, their changes are restricted to changes of state. Equations are not about specific values of the parameters or states; instead they jointly describe generic relations between parameters, states and the changes of states[4]. This is why changes of state of an object do not affect the validity of the equation which describe its behavior. For example, the mass is an element of the description of some generic objects, formalized by a generic variable m representing jointly and synthetically all the possible masses.
Physical objects, hence, are generic objects. More generally physical ‘laws’ are about generic objects. Consider for example the fundamental principle of dynamics: mass times acceleration equals the sum of external forces applies to the object. Here, the “external forces" are understood in a completely generic manner and any kind of forces may be involved.
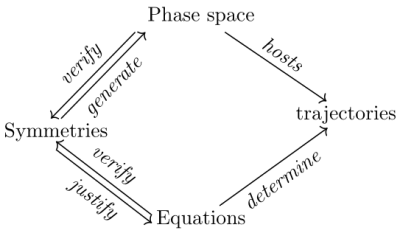
Typically, a physical object is described in a mathematical space which is generated by the various quantities required to describe this object. This mathematical space is called the ‘phase space’[5]. In classical mechanics, the phase space is the space of positions and momenta. This mathematical space is given in advance; it pre-exists the description of the object. The behavior of the physical object is defined as the way in which the object changes in its phase space. The space is also assumed to provide all the causes of the changes of the object, and thus it specifies the quantities that should be measured experimentally. In classical mechanics, positions and momenta, in combination with properties such as the mass, are the quantities required to understand the changes of positions and momenta over time.
A phase space, however, is not sufficient to understand the behavior of an object because the quantities it provides need to be articulated together to understand the changes of the object[6]. In physics, a theoretical framework requires equations that depend on the variables symbolizing the quantities describing the objects. The behavior of an object, that is to say its changes, is determined as a specific trajectory by equations that single it out in the phase space. Equations are valid for the phase space (or, at least, some regions of it) and depend on its quantities. The behavior of the object is completely determined by the quantities that define its phase space and the corresponding equations. Predicting a trajectory corresponds to making this trajectory mathematically remarkable. To this end, equations typically correspond to optimization principles (for energy, entropy, entropy production, etc.), which enable physicists to single out a trajectory, the optimal trajectory that the system follows according to the theory. Optimization principles and the ability to derive equations are essential for fundamental physical theories and special models to make predictions.
For the purposes of this paper, the key question to be asked at this point is what justifies the use of the spaces and equations in the theoretical constructions of physics. In part, these mathematical structures stem from axioms and are justified by their consequences. However, there is more to say on the nature of fundamental hypotheses of physics and the way in which they justify the use of mathematics.
Because whole classes of concrete objects are described in the same mathematical frame, they are studied as the same generic object, and all have the same behavior. As we evoked above, a piece of lead, an apple, or a planet are all the same objects from the viewpoint of classical gravitation: they all are point-wise objects with a position, a momentum, a mass, and they all are subject to the principle of inertia and gravitational forces, described by the same equations. In this respect, there is no relevant difference between them and they are described jointly and synthetically as the same generic object. At the core of this approach to natural phenomena lies the identification of non-identical objects. This identification of non-identical objects is made explicit by transformations that leave these objects invariants (i.e. symetries). Putting an emphasis on transformations is a modern approach in mathematics and physics that we build upon in this paper. In particular, invariants are best described by the transformations that preserve them and which make explicit a mathematical structure.
Generic objects are, for the most part, defined by the transformations that preserve them, and that enable us to define stable mathematical structures. We call such transformations ‘symmetries’. The notion of symmetry we use is more general than the concept of geometrical symmetry in a three-dimensional space. Yet, the underlying idea is the same: geometrical symmetries are transformations which leave a geometrical figure invariant. Rotating a circle around its center, for instance, does not modify the circle: it verifies a central symmetry[7]. Similarly, symmetries (in general) are transformations which leave the relevant aspects of an object invariant. For example, cutting an apple into two halves does not change the way it falls in the vacuum. Hence, an apple and its two halves are symmetric (they are the same) from the point of view of free fall in classical mechanics. Allometric relationships provide a biological example of symmetry (Longo and Montévil 2014b). In mammals, the average period of rhythms such as heart rate or respiratory rate is found experimentally to depend on mass with the relation τ ∝ M1/4. Measuring such relationships amounts to assuming that the basic properties of metabolism are preserved under the transformations consisting of changing sizes and species, and thus that mammals of different masses are symmetric as for their internal rhythms (West and Brown 2005; Longo and Montévil 2014b). Lastly, the assumption that different replicates of an experiment enable us to access the same situation also corresponds to an assumption of symmetry between the replicates: they are all supposed to behave in fundamentally the same way[8].
Symmetries are the basis of the mathematical structures in physics; that is the phase space and the relevant equations. Accordingly, they constitute fundamental physical assumptions which are less anthropomorphic than the notion of law and more meaningful than conservation principles (see for example Van Fraassen 1989; Bailly and Longo 2011; Longo and Montévil 2014a).
For instance, the choice of an origin, three axes and a metric are mandatory in order to write equations and perform measurement of positions and velocities (in Galilean, special, or general relativity). Although different choices are possible, the consistency of the theory depends on the fact that the trajectories obtained in different reference systems are, in a fundamental sense, the same: in particular, they are invariant under suitable classical or relativistic transformations of the reference system. Thus, the equations of physics are symmetric under these transformations[9]. In general, the same trajectory should be obtained before and after transformations which are fundamental symmetries in the theory,[10] and these symmetries enable us at the same time to formulate and justify the equations and the phase space.[11]
In short, physical objects are understood as generic objects that follow specific trajectories. Theoretical symmetries ground this approach to natural phenomena. The epistemological structure of generic objects is summarized in figure 1. In the next section, we discuss the principle of variation and the major challenges that biological variation raises when one tries to frame biological objects theoretically.
3 Variation and symmetry changes: biology as the domain of specific objects
A central and pervasive property of biological systems is their ability to change their organization over time[12]. These changes are not just quantitative changes, they are also qualitative. From a physico-mathematical point of view, qualitative changes typically imply changes of the relevant mathematical structures and, accordingly, changes of symmetries. For example, changes of states of matter in phase transitions typically correspond to changes of symmetries: a liquid is symmetric by rotation while a crystal is not, because of its microscopic structure (see figure 2).
In the biological domain, the organization of any current organism has been shaped by permanent qualitative changes, that is, through changes of symmetries. A given biological organization is determined by an accumulation of changes of symmetries both on the evolutionary and the ontogenetic times[13]. These changes correspond to changes in the manner in which functions are performed, or even to the appearance or loss of functions.
Acknowledging that organisms can vary in this strong, functional sense, is not trivial: historically, the preformationists (as for development), and the fixists (as for evolution) have held just the opposite view. If the homunculus is already in the egg, or, in modern terms, if dna already contains a blueprint of the organism, then development is just the unfolding of an already existing organism (with all its relevant properties and functions). Similarly, if species do not change over geological time, then obviously organisms conserve the same functions.
The idea that biological objects genuinely develop and evolve over time corresponds to the idea that the mathematical structures required to describe them also change over time. Thus, stating that development and evolution involve symmetry changes constitutes nothing more than a mathematical interpretation of the departure from the preformationist or fixist stances of development and evolution. Evolution is rarely considered as entirely determined as the unfolding of historical necessities. Similarly, development should not be seen as the unfolding of a pre-constituted organization but instead as a cascade of folding leading to the setting up of an organization (figure 2 and 3).

Figure 2: Scheme of an elementary symmetry change in biology. An initial situation, on the left, is described by analogy with physics (see figure 1). However in biology, variation can escape such a frame. Understanding the object then requires a change of symmetry and of the whole mathematical structure framing the object. Trajectories are at the center of this change, they escape the initial frame and thus require a change of the symmetries describing the object.
The crucial consequence of this view is that, because of their permanent symmetry changes, biological objects should not be considered as generic objects. Organisms are not well defined as invariant under transformations. When an organism is transformed, and in particular when the flow of time operates on it, the organism may undergo unpredictable qualitative changes. As a result, biological objects are not well described by the virtuous cycle described in figure 1. Accordingly, trajectories are not entirely framed by a mathematical framework: they may escape such frameworks and require a change in the symmetries, space of description, and equations used to describe the object (figure 2).
We propose then to understand biological objects (and organisms in particular) as specific objects.[14] Specific objects are constituted by a particular history of relevant and unpredictable symmetry changes over time, at all time-scales. Specific objects can be understood as the opposite of generic objects: two instantiations of a specific object may always differ by at least one of their relevant qualitative aspects (in a given theoretical frame), while two instantiations of a generic object do not. For example, two organisms, be they clones, may always differ in one of their relevant qualitative properties, for instance because they may have undergone differences in their morphogenesis, i.e., they have been constituted by different developmental histories.
On the basis of the concept of specific objects, we can now state the principle of variation:
Principle of variation:
Biological organisms are specific objects.
The principle implies that biological organisms undergo changes of symmetry over time and that, as we discuss below, some of these changes cannot be stated in advance[15]. In other words, the mathematical structure required to describe organisms is not stable with respect to the flow of time. Qualitative changes of structures and functions occur over time and some of them are unpredictable.
We now expand on several aspects and implications of the principle of variation.
3.1 Randomness proper to specific objects
A fundamental feature of the principle of variation is that it includes an original notion of randomness: the very fact that biological objects undergo unpredictable symmetry changes. Generally speaking, the notion of randomness is often conflated with the idea that events have some probability of occurrence. However, scientific approaches to randomness are richer than the notion of (classical) probabilities (see for example Longo, Palamidessi, and Paul 2011 for a discussion at the crossroads of different fields). Randomness may be defined generally as unpredictability with respect to a theory. The notion of randomness which stems from the principle of variation is not endowed with a probability measure.
Let us first characterize randomness in the case of a basic symmetry breaking, typically encountered in physical models. Let us start with a situation which is symmetric, for example a gas (figure 3, top). All directions are equivalent for this object: all macroscopic quantities (density of the gas, pressure, etc.) stay the same after rotation. When the symmetry is broken, directions are no longer equivalent; for example, there are privileged directions corresponding to a crystal structure after a phase transition (figure 3, bottom). The symmetry of the initial situation means that all directions are initially equivalent and then that it is not possible to deduce the subsequent privileged directions in the crystal. As a result, the directions of the crystal are random in this theoretical account. Moreover, since all directions are symmetric in the initial conditions, all directions have the same probability to become one of the crystal’s privileged directions.
This physical situation exemplifies how symmetry breaking and randomness are associated and how the initial symmetries define and justify probabilities (see Longo and Montévil, n.d. for a general analysis of this association).

Figure 3: Example of a symmetry breaking. The left pictures correspond to an initial situation and the right ones to the same situations after a rotation (represented by the arrows). The above diagrams show a disordered situation such as a gas or a liquid. This situation is statistically symmetric by rotation, there are no privileged directions. By contrast, the situation below corresponds to a crystal such as graphite. It is not symmetric by rotation (except with an angle of 180∘) and it thus has directions which have an intrinsic physical meaning. The transition from the situation above to the situation below implies the introduction of new relevant elements: the directions of the crystals, which are random.
Symmetry breaking and the associated randomness are relevant for biology but we submit that they are not sufficient. Biological randomness includes a fundamentally different notion. In the above case, the possible outcomes (all the possible directions in three dimensions) are defined before the symmetry breaking, as it is the mathematical space on which symmetries act. Saying that the gas is symmetric by rotation requires us to define rotations and therefore the set of all possible directions on which rotations act. In biology, in contrast, the principle of variation poses that the list of possible outcomes and therefore the relevant symmetry changes are not pre-defined. For example, it is not possible to embed all the spaces of description of current and future organisms within the space of description of the last universal common ancestor (LUCA). A part of the relevant symmetry and symmetry changes can only be listed a posteriori, that is, after their realization. These changes only make sense as a result of a previous history. Not only lineages, but also individual organisms, are subject to biological randomness, as their development can sometimes take new routes which were not expected in advance (e.g. West-Eberhard 2003).
Note that we consider symmetry changes in general and not just symmetry breaking. Symmetry breaking corresponds to symmetry changes which start from a situation that respects a given symmetry to a situation where this symmetry is no longer valid, as discussed above. Other symmetry changes are possible, for example one can go from an asymmetric situation to a symmetric one. In biology, symmetry changes include the appearance of new and unpredictable symmetries corresponding to new relevant parts and their functioning. For example, the appearance of sexual reproduction in evolution corresponds to a separation of individuals in two genders in many species, where new symmetries (or equivalence) between males on one side and females on the other become fundamental as for their role in reproduction. New associated variables become relevant, for example the sex ratio of a population.
Because of symmetry changes, the phase spaces of biological objects also change in unpredictable ways over time. Symmetry and phase space changes constitute a specific form of randomness, proper to biological systems (Longo and Montévil 2012, 2013; Longo, Montévil, and Kauffman 2012; Kauffman 2013). Biological randomness typically manifests itself through the appearance of new relevant quantities, parts, functions, and behaviors over time (for example limbs, toes, toenails, all the quantities required to describe them and the various functions that they can have).
3.2 Constraints and specific objects
The principle of variation does not preclude the presence of elements of stability in biological systems. On the contrary, in order to show experimentally and describe theoretically a change of symmetry, the preceding and following situations have to be stable enough to be described. In other words, a set of symmetries has to be at least approximately valid long enough before it changes for an observer to discuss it and after the change the new set has to be met for some time too. For example a given geometry of bones is conserved during movements of the organism at short time-scales, which corresponds to the conserved symmetry of a solid (the relative positions of points in a solid do not change). However, this geometry is plastic at longer time scales and very important changes can occur especially during development (West-Eberhard 2003). The change of two bones geometry at different times thus corresponds to a symmetry change, but the symmetries of these bones are met at short time-scales.
We call constraints the relevant stable elements at work in biological systems and their associated symmetries. Constraints are local stable elements, in the sense that they only concern a particular aspect of a given organism. In addition, constraints are contingent insofar as they, and their associated symmetries, may change over biological time (which is implied by the principle of variation).
In short, we define constraints as symmetries (i.e. stable mathematical structure) witch have a restricted range of validity and are used to describe a part of a specific object.
3.3 Constraints and randomness
In this section, we discuss the articulation between two kinds of randomness in specific objects. This discussion is more technical and may be skipped in a first reading.
A constraint (or a combination of constraints) exerted on biological dynamics may lead to a situation in which symmetry changes (if any) occur in a generic manner, typically as symmetry breaking. In the case of generic symmetry changes, these ‘random’ changes can be stated in advance, even though their specific outcome cannot. This randomness can be derived from constraints, and it is weaker than the randomness proper to specific objects.
Let us start with morphogenesis as an example. Most (if not all) mathematical models of morphogenesis involve a symmetry change, which usually is a symmetry breaking. Consider for instance Turing’s model of morphogenesis (Turing 1952)[16]. In this model, the equations describing reactions and diffusion of chemicals remain invariant, so that their properties (rate of reactions, coefficient of diffusion, etc.) are stable constraints. In turn, these constraints lead together to a symmetry breaking, because of the sensitivity of the non-linear dynamics to initial conditions (an instability, says Turing): minor fluctuations trigger different outcomes.
Another very different example of biological symmetry breaking is the dna recombinations in the maturation of lymphocytes (Thomas-Vaslin et al. 2013). The random process of recombination in a cell can be seen as a symmetry breaking from a situation where all the recombinations to come are equivalently possible to a situation where only one recombination is actually realized in each cell. After recombinations, the description of the system has to include which possibility each cell has “chosen”. This symmetry breaking makes the diversification of the immune repertoire possible under the constraint of enzymes.
Both cases (morphogenesis and dna recombinations) involve stable constraints, in an extremely sensitive process, which leads to a change of symmetry. These constraints are stable parts of the organization of the considered organisms. As a result, the associated changes are robust in the sense that they will occur as a consequence of these constraints. In such situations, a generic change of symmetry is established, which generates “new” relevant quantities but in a generic manner, i.e. the change belongs to a set of predefined possibilities. These new quantities are new in a weaker sense than the unpredictable new dimensions of description that specific objects can generate. For example, the recombinations in the immune system can be seen as generic, as a set of possible physico-chemical recombinations of molecules. The outcome of such recombinations is probably unique because the odds of performing the same recombinations twice are vanishingly small, but this outcome is still generic. The situation is analogous to the physical case of the positions of individual molecules in a gas which are basically unique, whereas the gas is still in a generic configuration because the gas is in a configuration of maximum entropy. However the actual immune repertoire in an adult mammal is not fully determined by the generic properties of recombinations because the recombinations are just a part of the process establishing this repertoire. The immune repertoire strongly depends on the specific history of the given organism, its environment, non-genetic inheritance (through milk and the microbiome), etc. (Thomas-Vaslin et al. 2013). The immune repertoire has a causal structure that is not determined by pre-existing regularities. The dependency on the organism’s history is functional, it determines the immune response to specific pathogens and contributes to the dynamic relationship with the microbiome. The biologically relevant properties of the immune repertoire are not the generic properties of recombinations, instead they are the specific properties which stem from a history. Hence, the actual repertoire of the adult contains more meaningful novel structures than the initial probabilistic recombinations.
Now, every time we describe a symmetry change according to current physico-mathematical methodology, it takes a generic form, that is, a possible change in a pre-given space of possibilities which may be given a priori probabilities. Biological objects are — by hypothesis — specific, but when we describe a particular change of symmetry, it is studied a posteriori as a generic aspect of the object, and can be added to the past possibilities of a system. Randomness is then not correctly framed by a priori probabilities. Probabilities, if any, are defined a posteriori. A specific possibility is accommodated by the space of possibilities, but this space is obtained a posteriori and obviously does not include all future possibilities.
Let us unpack this idea. A physical symmetry breaking is a simple elementary process: a symmetry is met by the system, and after the symmetry breaking event, the symmetry is no longer met. The possible breakings are given by the initial set of symmetries and make mathematical sense when they can be described in a given mathematical space where the symmetry operates. However, if a situation is and always has been completely symmetric, the symmetries do not change anything and thus, cannot be properly evidenced as transformations (because the object is not changed at all). Thus the logic required to describe a new symmetry breaking has two steps. First the symmetry that will be broken has to be added to the initial definition of the system and accordingly the states that are initially symmetric have to be added to the phase space of the object. They are added because they are required to accommodate their future breaking. Then, and only then, may the symmetry be broken. Such a modeling is retrodictive: the mathematical space, needed for an equational model, can be given only after the change has been observed. In general, then, a biological dynamic must be understood as a possible path, out of many established along the biological dynamics, which consists in the composition of stepwise symmetry changes.
In a given situation, some symmetry changes can be spelled out and analyzed in a generic framework because they are stabilized by (local) constraints. Let us consider such an elementary biological symmetry change, for example in a morphogenesis model. We can describe it explicitly with generic constraints but it is also possible to leave it implicit and consider that this single symmetry change is taken into account by the specificity of the object, among many other changes. The choice depends on the perspective adopted to understand a given situation, including the scale of description and the phenomena of interest. For example, the intestine folding are usually kept implicit when studying brain morphogenesis.
Even though the boundaries of specific and generic aspects of an organism are relative and may change after a new possibility is acknowledged or as a result of a change of perspective, the accurate description of any biological organism will always involve a component of specificity. In a given representation of an organism, all changes of symmetry are then either accommodated by the specificity of the object or by generic symmetry changes. The concept of the specificity of biological objects aims to enable us to take into account theoretically all symmetry changes without spelling out all of them explicitly.
3.4 Historicity
Historical objects are objects whose properties are acquired or lost over time, and cannot all be described ahead of time. The fact that biological organisms are specific objects straightforwardly implies that they are historical objects and, in particular, contingent objects in Gould’s sense (Beatty 1995; Gould 1989). Historicity thus goes hand in hand with biological randomness, which corresponds to the fact that a situation after a random event cannot be stated with certainty before the event. Thus, a system showing biological randomness shows historicity: the object takes a particular path among several possible paths through time. Reciprocally, historical objects necessarily show some randomness.
Let us first consider an analogy with dynamic systems. We can see a trajectory defined by a differential equation as the sum of infinitesimal changes from the initial conditions to any time point. By analogy, it is conceivable to see biological historicity as a sum or a sequence of variations since the origin of life. However, this idea does not have a well-defined mathematical and theoretical sense, insofar as such a history is not entirely accessible. Nevertheless, it is still possible to clarify the present in the light of the past — and, as a matter of fact, this is precisley one of the aims of evolutionary theories.
As discussed in (Longo et al. 2015), although historical objects exist also in physics, they are historical in a weaker sense. Self-organized physical objects, for instance, are sometimes described as historical, mostly because they depend on a symmetry breaking. For example, the appearance of convection cells in a fluid corresponds to a qualitative change in the macroscopic dynamics of the fluid. Nevertheless, self-organized objects are spontaneous: they can be obtained de novo. Theoretically, they can be described as the spontaneous self-organization of flows of energy and matter. Even the physical situation of the early history of the universe can be obtained experimentally “just” by tuning a parameter (by obtaining very high local densities of energy with particles accelerators)[17].
Despite these analogies though, physical self-organizing processes have no historical or evolutionary time in a strong theoretical sense; they may just have the time of a process. They entirely obey optimality principles from physics and past events have not shaped their properties, insofar as the symmetry breakings that self-organizing processes may encounter are all pre-defined within the theory. A hurricane does have, so to speak, a “birth”, a “life”, and it does eventually “die out”; yet, hurricanes have been the “same” kind of object for the past four billion years on Earth. Again, their time is that of a process. Their historicity is embedded within a pre-defined phase space.
The fact that we can understand such spontaneous objects on the basis of a stable generic mathematical structure is not fortuitous. Indeed, their spontaneous character corresponds to the fact that these objects can emerge from homogeneous initial conditions in the mathematical framework used to describe them. By contrast, specific objects are not framed by stable mathematical structures: they cannot be derived from homogeneous initial conditions and cannot be obtained spontaneously in practice. Even in the “origin of life” field, the aim is to produce a cell which can evolve and not a cell that is similar to all current cells as they have evolved for billions of years. Moreover the aim is certainly not to obtain a cell similar to any specific species (Pross and Pascal 2013).
According to the principle of variation, biological objects are the result of a cascade of unpredictable symmetry changes, which implies that they do not follow optimization principles and that they are not spontaneous. To be sure, biological objects did appear spontaneously in the history of life, but should one re-run the history of the Earth, one could not expect to obtain the same biological objects. It is not even possible to state in advance the mathematical space of possible forms that could be obtained. The historicity of biological objects is not embedded within the phase space anymore (as it was in physics): rather, the principle of variation means that the phase space itself is historical (figure 3).
At first sight, though, the claim that the phase spaces in biology are historical seems too strong: aren’t there some aspects of biological objects which are ahistorical? Evolutionary convergences, for instance, seem to be an example of an ahistorical aspect of the living: convergent features seem to be obtained independently of (some aspects of) the past history of the organism. Let us first point out that evolutionary convergences are not about invariant properties of a given object over time, they are about mathematical structures that are similar in different historical paths. Let us consider the case of the camera eye of the vertebrates and of the cephalopods as an example. These eyes have different evolutionary origins but they are nevertheless similar and one could argue that they would be instances of the same generic object from a physicomathematical viewpoint, when described in terms of optical geometry for example.
The principle of variation, however, implies that the convergence is very unlikely to be qualitatively exact. There would always be a relevant biological description which would distinguish them sharply by pointing to differences in their organization and in their articulation with the rest of the organism. For instance, the retina is inverted in vertebrates: the axons of photoreceptors and their connection to ganglion cells and the optic nerve are located between the receptors and the light source, creating a blind spot at the level of the optic nerve. In cephalopods, axons are behind the photoreceptor which does not create such a blind spot. A close analysis of both the phylogenetic and the ontogenetic paths makes the difference understandable: the high modularity of the cephalopods’ brain derives from an early separation of the brain’s modules by an invagination of the ectoderm, in contrast to the evagination of the diencephalon, due to the late separation of the eye component of vertebrates’ brains.
In short, the principle of variation implies that strict evolutionary (or developmental) convergence never occurs: symmetry changes are such that biological objects drift in a burgeoning phase space, and partial convergences always embed hidden differences which may be of importance with regard to the considered behavior of the biological object in that phase space. Reciprocally, the similarity between the organizations of different organisms stems from common descent, that is to say from a shared history.
3.5 Contextuality
Organisms are contextual objects. In our theoretical framework, the symmetries of organisms depend on its environment — both on its immediate environment and the environments encountered in its past history.
The fact that the symmetries of an organism depend on its immediate environment constitutes another similarity with self-organizing physical systems mentioned above, as the latter strongly depend on their boundary conditions. However, the principle of variation makes the contextuality of biological objects more fundamental than that of physical systems. Contrary to physics, the possible changes of symmetry due to a change of the context are not all pre-defined. This means that an organism in a new environment may undergo unpredictable reorganizations, which correspond to different relations between its internal constraints and the environment, as well as different relations between its internal constraints, tout court. For example, we do not know a priori the many changes that can occur when bacteria that used to live with many other species in their natural and historical environment are grown as an isolated strain in laboratory conditions. Similarly, it is always difficult to assess whether the behavior of cells cultured in vitro is an artifact of in vitro culture, or whether it is biologically relevant (meaning that it corresponds to a behavior that happens in the context of the multicellular organism from which they were taken, see Montévil et al. 2016).
The contextuality of biological objects is coupled with their historicity (Miquel and Hwang 2016): biological organizations tend to maintain the effects of former environments and may even internalize their relationship with the environment over time. This holds at the developmental scale (think of how early plastic responses to the environment might be ’frozen’ later in development, see also (Gilbert and Epel 2009)), at the scale of several generations (for example through epigenetics), and at longer evolutionary scales (think, for instance, of the presence of lungs and lack of gills in marine mammals, which reflects a past terrestrial life).
Let us discuss two examples of internalization of the context on the developmental and on the evolutionary time scales, to show how it can lead to unexpected behaviors of biological objects.
On the developmental time-scale, an example of internalization of past contexts is provided by the response of cells to hormones (Soto and Sonnenschein 2005). Basically, the response of a cell to hormones does not depend only on the specific receptor and corresponding hormone involved but, rather, on the developmental history of this cell. More precisely, precursor erythroid cells are expected to differentiate into red blood cells when their erythropoietin receptors bind with erythropoietin. However, precursor erythroid cells which have been engineered to lack erythropoietin receptors and instead have receptors for prolactin do differentiate into red blood cells when they are exposed to prolactin, a hormone associated with lactation (Socolovsky, Dusanter-Fourt, and Lodish 1997). Conversely, mammary epithelial cells can be engineered to have a hybrid receptor with an extracellular part of a prolactin receptor and an intracellular part of an erythropoietin receptor. These engineered cells respond like normal mammary epithelial cells to prolactin (Brisken et al. 2002). These examples show that it is not the molecular specificity of a signal binding to a receptor that determines the response of a cell to a hormone. In contact with a hormone for which it has a receptor, a cell rather responds according to the context of its cellular lineage during development, that is its trajectory in time and space (Soto and Sonnenschein 2005).
On the evolutionary time-scale, a component of an organism, as a result of a history, may be used for different purposes in different contexts. The phenomenon of a character (be it the result of past natural selection or not) which is coopted for a current use has been named ‘ex-aptation’ by Gould and Vrba (1982). They provide many key examples, for instance: “the jaw arises from the first gill arch, while an element of the second arch becomes, in jawed fishes, the hyomandibula (suspending the upper jaw to the braincase) and later, in tetrapods, the stapes, or hearing bone” (Gould 2002, 1108). An ex-aptation is a re-interpretation, or re-use, of a trace of the past in a new context and, therefore, cannot be derived from the initial function of the parts involved. As a consequence, the detailed structure of the internal ear can be better understood by looking into the cumulative history of ex-aptations.
In light of the principle of variation, the internalization of current and past contexts provides one way (although not the only one) in which symmetry changes can occur throughout the history of an organism. As an illustration, the internalization of the context contributes to explaining the difficulty of replicating biological experiments, insofar as aspects of an experimental situation which can be relevant to the studied behavior may not be measured and can be traces of an (unknown) past (Begley and Ellis 2012).
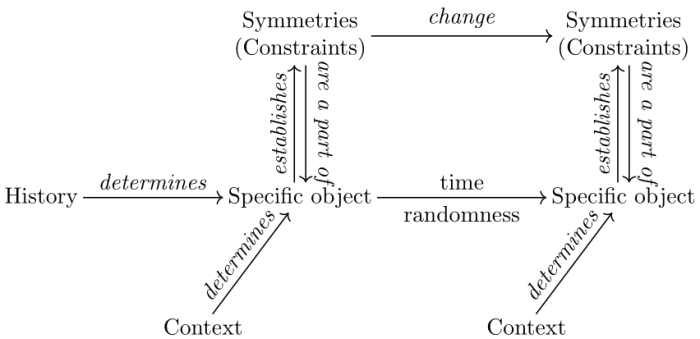
Figure 4: Biological objects and their theoretical structure. Specific objects are not defined by invariants and invariant preserving transformations. Instead, specific objects such as organisms undergo random variation over biological time. Their behaviors are not given by a synchronic description. Instead, they depend on a history and a context. Constraints are restricted invariants and symmetries, which may change over time and frame a part of the behavior of specific objects. Experiments and mathematical models usually investigate constraints and their changes.
3.6 Variability
The principle of variation underlies biological variability: the fact that multiple organisms or the same organism or lineage at different times exhibit differences when compared to each other.
The flow of time is the most fundamental transformation acting on biological objects: as we argued, biological symmetries and accordingly biological organizations are not preserved as time passes.
Variability tends to be stronger when considering large evolutionary time scales than for shorter time scales. When one follows the succeeding generations from the LUCA to a randomly chosen current organism, for example a rat, many relevant aspects of the description needed to understand these organisms appear and disappear through time.
Variability is also significant at physiological time scales, even at those that are much shorter than the lifespan of the considered organism. Heart rate, for example, does not obey homeostasis stricto sensu: the beat to beat interval is not invariant (in a healthy situation), and it does not even display fluctuations around a stable average value. Instead, the beat to beat interval fluctuates in a multiscale manner (West 2006; Longo and Montévil 2014b). Typically, the heart rate of a healthy subject displays patterns of accelerations and deceleration at all time scales during wake hours. Note, however, that the typical symmetries of multiscale fluctuations (scale symmetries) are not met either. Rather, many factors impact the multiscale feature of these variations of rhythms. For example, the current activity of the subject, her age, her life habits (smoking, exercising, etc.) and diseases change these multiscale features (Longo and Montévil 2014b). These differences in the patterns of the variability of the beat to beat interval can even be used for diagnostic purposes (West 2006; Bailly, Longo, and Montévil 2011).
Besides the flow of time, the second set of transformations relevant to variability are the permutations of different organisms or different populations. Permutations correspond to the interchanging of different objects. They are fundamental symmetries in many physical frames: for example, it is axiomatic that all electrons follow the same equations (but they can be in many different states). In experimental biology, permutations of different animals or cells are often assumed to be symmetries: when one considers different animals of a control group, a common assumption is that they behave in the same way and that the quantitative variation observed stems from a probability distribution that would apply to all of them. This assumption, in one form or another, is required to apply theorems of statistical analysis.
According to the principle of variation, however, the permutation between these organisms cannot be taken as a symmetry. Of course, organisms are related by a shared history, which enables us to determine that they are mice, rats, etc., of a given strain. Yet, the transformation which replaces one organism by another in the same group corresponds to a comparison between the results of divergent paths stemming from a shared history. Here, divergence is taken in a strong sense and implies symmetry changes and not mere quantitative changes conserving the same symmetries. For example, qualitative behaviors differ between different strains of the same species, even in unicellular oganisms (Vogel et al. 2015). Now, we illustrate this idea with a historical example.
At the end of the 19th century, Sir Francis Galton, one of the founders of the notion of heredity, came up with a device, known as the bean box or the quincunx (see figure 4). The quincunx facilitated the simulation of a binomial distribution (the device would be used to simulate “normal variability”, Galton (1894, 63f)). The device consisted in a vertical frame with three parts: a funnel in its upper part, rows of horizontal pins stuck squarely in its middle part, and a series of vertical compartments in its lower part. A charge of small items (say, beans or balls) would be thrown through the funnel, travel through the pins, possibly bouncing in any direction, and would be gathered by the vertical compartments at the bottom (where they would not move anymore). In the end, the distribution of the items in the bottom compartment would approximate a binomial distribution.

Figure 5: Galton’s quincux (Galton 1894, 63). A ball falls but obstacles lead it to move randomly to the right or to the left. The outcome is variability in the position of the balls at the bottom of the device. This device illustrates variation in a pre-defined set of possibilities. Biological variation, by contrast, sometimes involves the constitution of new possibilities, which would amount for the ball to jump outside of the quincunx.
In our terms, the bean box works the following way. The items share a common history when they get into the funnel, and this common history leaves a trace in the result: depending on where the funnel is placed into the device (e.g. in the middle or not), the distribution of the items in the end varies. When the items exit the funnel, they take divergent paths (by bouncing on the pins) until they reach a vertical compartment. This is, however, divergence in a weak sense. For the bean box to work, all the items have to be supposed to be symmetrical, and all the realized paths have to be supposedly taken from the same underlying distribution. As a matter of fact, this assumption is necessary for the use of statistics in biology: when performing an experiment on — say — rats, one supposes that all rats are independent realizations of a random variable taken from the same underlying distribution and that this distribution is stemming from their most recent common ancestor. The most recent common ancestor plays the role of the funnel; and subsequent mutations, effects of the environment, spontaneous variations, etc., play the role of the pins. Variation can occur, but it will be merely quantitative and measured by the position on the horizontal axis in the bean box.
By contrast, the principle of variation posits that unexpected (and unknown) qualitative variation permanently occurs. This means that different organisms are not different realizations of a random variable taken from an underlying single distribution, as this distribution cannot even be defined. In terms of the bean box, this means that the pins unexpectedly open new dimensions (i.e. new relevant features arise), which would not be defined before the realization, and would not be reproducible after either. This is what we mean by divergence in a strong sense. Galton used his device to illustrate normal variability where variability would be quantitative, in a pre-defined space. By contrast, the principle of variation implies that variation can be qualitative (i.e. symmetry changes) and that the space of variation is not pre-defined. This, to reiterate, applies both at ontogenetic and phylogenetic scales[18].
3.7 Modelization and specific objects
Current mathematical modeling practices in biology borrow mostly the epistemology of physics and are based on generic objects following specific trajectories. So far, we have argued that the theorizing of physical phenomena is based on stable mathematical structures and on the corresponding analysis of generic objects. We advocate, by contrast, that biological organisms are specific objects moving along possible phylo-ontogenetic trajectories. Organisms have a historical and contextual nature and change their organization and functions over time.
This physicomathematical modeling practice in biology leads to many technical and epistemological problems. For example Boolean networks (see Kauffman 1993) are used to model gene networks and are defined as random networks where the existence of an edge between two nodes follows a given probability distribution. Such an assumption is a way to model protein or gene networks in an ahistorical manner (and for example to generate them de novo in simulations). This disregards the fact that the actual phenomena are the result of evolution, and thus that actual biological networks depend on the historical interplay between living beings and their environment, even at the molecular level (Yamada and Bork 2009). Hence, they are not a sample of a random network following a given probability distribution. This is also true for cell networks: in a tissue, cell to cell interactions or the production of proteins are largely a context- and history-dependent phenomenon. For instance, the “normalization” of a cell transferred from a cancer tissue to a healthy one can be understood as the effect of tissue context (and its history) controlling individual cellular activities (Soto, Sonnenschein, and Miquel 2008; Sonnenschein and Soto 2016). These examples show that the standard modeling strategies of a biological system struggle against the historicity and contextuality of biological organisms.
We interpret the “big data” approach, that aims at taking into account a massive amount of data in a model, as an attempt to address the consequences of the historical nature of biological objects while keeping the physical methodology of establishing intelligibility on the basis of generic objects. Such an approach, however, raises the question of the intelligibility of their object, because the complicated mathematical structures of models based on big data make only computer simulations possible. Other more physical approaches focus on generic features that even these historical systems would meet. For example, scaling laws in networks have been extensively investigated, but their validity is criticized (Fox Keller 2005). Globally speaking, however, the methodological emphasis on generic features implies that the biological meaning of specific variations, and their role in a given organism, is lost. The issue is that without stable generic features, the question of the objectivity of these models is open, insofar as their description and behavior will have a high degree of arbitrariness: the models will miss the consequences of the principle of variation and, thereby, display invariants which are not valid.
Most mathematical models do not aim at capturing features of whole organisms but, rather, at singling out some constraints, corresponding to specific parts of an organism. Typically, they focus on the morphogenesis of an organ or a tissue, for example the formation of leaf disposition (phylotaxis) (Douady and Couder 1996), the organization of the cytoskeleton (Karsenti 2008), the morphogenesis of vascular networks (Lorthois and Cassot 2010), etc. Even though this approach has obvious merits and has provided remarkable insights, it does not take into account that these organs or tissues are parts of the whole organism and that the possible reorganizations of these parts are essential to variability, development, and evolution. From a mathematical viewpoint, one aspect of this weakness can be expressed as the fact that models miss some degrees of freedom corresponding to the changes of phase space that follow from changes of symmetry, in accordance with the principle of variation.
Although mathematical models are more and more used in biology, we think that the key challenges raised by biological organisms, in particular variability, historicity and contextuality, have not yet found a proper methodological and epistemological treatment. We hope that the principles discussed in this issue will contribute to better identify and address these challenges.
3.8 Conclusive remarks on the principle of variation
The principle of variation leads to a change of perspective with respect to physics. Historicity, contextuality, and variability are fundamental every time an organism is under scientific scrutiny. Rather than trying to avoid the intrinsic difficulties in mathematizing these features, our theoretical frame aims at building on them. To be sure, the randomness of symmetry changes limits the actual knowledge we can obtain on a given organism. At the same time, however, this new kind of randomness can be studied as such, and opens up new avenues of investigation.
Last, underpinning our discussion above is the fact that the principle of variation involves two kinds of changes: changes of the biological object itself (philosophers would say this is an ontological change) and changes in the question asked about this object (philosophers would say this is an epistemological change). For example, developmental biology studies features that appeared with multi-cellularity: the field is thus a result of biological variation. Reciprocally, growing cells in lab conditions comes with modifications of their behaviors which in turns affects the questions at stake and possibly their future culture conditions. Thus, in our view, the instability of biological objects goes hand in hand with the instability of biological questions: they co-constitute each other.
4 Bringing organization into the picture
Let us begin with a methodological remark on the articulation of the principles of variation and organization. The theoretical definition of a biological organization at a given time is closely related to how it may change, and that for two related reasons. First, the organization of every current organism is the result of a cascade of changes over ontogenetic and evolutionary time scales. Second, the appropriate theoretical definitions and representations of scientific objects are, generally speaking, those that enable us to understand the changes of these objects. For example, positions, momenta, and the mass are both necessary and sufficient to understand the changes of position of the planets of the solar system in classical mechanics. This justifies the theoretical representation of the planets on the basis of these quantities. In this respect, an appropriate framework for organisms requires the articulation of organization with the changes that it may undergo. To some extent, this question has been neglected in the past insofar as biological organization has been mostly approached as a mathematical fixed point, which leads to the concept of organizations as maintaining themselves identically over time.
4.1 Organization grounds constraints in specific objects
Even though organisms should be understood as specific objects, as the principle of variation posits, we would argue that some of their parts exhibit generic features in a restricted sense. As mentioned in section 3.2 above, we refer to these parts as constraints. More precisely, constraints are characterized as entities that control biological dynamics (processes, reactions, etc.) because of some symmetrical (conserved) aspect which they possess at the relevant time scales. For example enzymes are not consumed in a chemical reaction that they nevertheless change completely. Similarly, the geometry of the vascular system is conserved at the time scale of blood transport, and this transport is constrained by the vascular system.
The stability of constraints, however, has to be explained by a sound theory of biological organisms, especially in the long run. Indeed, beyond the time scale at which a constraint operates, constraints undergo degradation. A constraint may be further stabilized by a process being under the control of another constraint, which is itself stabilized by another constrained process, and so on: if the chain of dependencies folds up and the constraints can be said to be mutually dependent, the system of constraints is organized. The constraints that constitute an organism are the organized ones, which (i) act on a process stabilizing a constraint of the organism and (ii) depend on at least another constraint of the organism. The key aspect in this framework is that constraints are stable at a given time-scale, while being stabilized by processes taking place at other time scales, so that constraints behave as local invariants with respect to the processes they constrain.
However, while the time scales of constraints in the principle of organization are the intrinsic time scales of the processes and constraints under study, they do not preclude a change at these or other time scales for reasons extrinsic to these objects. Changes of organization stemming from the principle of variation can alter a constraint at any time scale. In this event, the former constraint may lose its status of constraint or may operate differently.
The cohesion of organisms is one of their fundamental features, and this cohesion has been the object of many theoretical investigations, for example as autopoiesis (Varela, Maturana, and Uribe 1974) or as work-constraints cycles (Kauffman 2002). Following this line, we argue that biological organisms realize closure of constraints (Montévil and Mossio 2015; Mossio, Montévil, and Longo 2016): functional parts of organisms act as constraints on each other, and they realize a mutual dependence. Closure is basically the circularity in the relation of dependence between constraints. The principle of organization that we propose states that the constraints of organisms realize closure.
We postulate that the stability of functional constraints hinges on their mutual dependence (Montévil and Mossio 2015; Mossio, Montévil, and Longo 2016), so that the overall stability of biological organisms is justified by the closure of constraints. When we consider the principle of organization and the principle of variation together, constraints are contingent in two complementary ways. They are contingent because of their historical nature and because their existence depends on the circularity of closure instead of being grounded on other stable first principles.
4.2 The epistemological status of closure under variation
By relying on the principle of organization, it is theoretically meaningful to work on sets of constraints that verify closure. Following the principle of variation, however, constraints are not necessarily conserved over time and may undergo changes which cannot be stated in advance. As a result, the validity of closure must extend beyond a given configuration of constraints. The validity of the principle of organization should not be understood as based on a given set of constraints (or invariants) which would happen to realize closure. Accordingly, the principle of organization is not deducible from a set of invariants and symmetries (as in “physical laws”), rather, it is the condition of possibility for the existence and persistence of biological constraints (i.e. local invariants and symmetries). For this reason, we suggest that closure constitutes the principle of organization that, alongside variation and other principles, frames the biological domain as a whole (see Montévil and Mossio 2015; Mossio, Montévil, and Longo 2016).
In epistemological terms, stating that the principle of organization is a fundamental principle implies that it cannot be deduced from underlying stable symmetries and becomes an (irreducible) theoretical principle for biological organisms. Closure becomes an a priori that replaces the a priori of space and time in physics, or, more precisely, of the phase spaces of physical theories.
In a theoretical sense, the generality of biological analysis is made possible by the permanent relevance of organization as closure, despite the continual symmetry and phase space changes. To a certain extent, the situation of closure is similar to that of the energy of a physical system being conserved despite its permanent changes of state. In the case of a change of constraints, an organized object goes from one closed regime to another, unless the organism does not succeed in establishing a new regime and dies.
4.3 Relevant variation with respect to closure
The principle of organization understood as the closure of constraints leads to the idea that the relevant changes of the organism involve constraints subject to closure. The changes of constraints that do not impact the constraints subject to closure fall in two categories: those that affect the environment and those that affect the organism (in other aspects than the constraints subject to closure). If a change of constraint affects the environment, it may be biologically relevant, for example if it affects other organisms. If the change affect the organism, but not its organized constraints, then it is not significant for the organism in the light of the principle of organization: these constraints do not play a role in the biological system (although they may be involved in an unpredictable organizational change).
As for the changes that may affect the organization, a general distinction can be made between irrelevant and functional variations. On the one hand, processes and constraints may undergo irrelevant variations, for example small quantitative variations, i.e. quantitative fluctuations that neither undermine nor modify the overall organization. This is variation that, in a word, the organism does not need to control in order to ensure its stability, by hypothesis. On the other hand, variation can be functional, in the sense of resulting in a change of one of more constraints, of their relations, and hence of the very organization. Examples of quantitative variation are for example moderate differences in the weight of some organs like the liver, or in enzyme concentrations; examples of functional variations are the reshaping of bones and musculature to perform a new function or to perform differently an old function (West-Eberhard 2003). Of course, the quantitative variation of a given constraint can also be potentially functional, in the sense of enabling the possible further emergence of functional variation, including pathological ones.
Another example of functional variation is random gene expression, which has been studied both in unicellular (Eldar and Elowitz 2010) and multicellular organisms (Dueck, Eberwine, and Kim 2016). In this literature however, functional variation is mostly understood in an evolutionary sense, while closure provides a systemic interpretation of functions (Mossio, Saborido, and Moreno 2009). As a result, closure enables us to conceive functional variation that is not necessarily inherited, provided that the constraint resulting from variation is still subject to closure.
4.4 Closure remains closure under variation
As discussed in (Mossio, Montévil, and Longo 2016), closure contributes to making both internal and external variations possible. The circularity of closure weakens the coupling between what is going on inside a system and its boundary conditions (Barandiaran and Moreno 2008). Such a decoupling enables variation beyond what would be permissible if the system were completely determined by its boundary conditions (such as in physical self-organization). Reciprocally, an organism can stand a relatively unstable ecosystem because of its autonomous stability due to the closure of constraints.
Under our principles, functional variation cannot lead to a violation of the organization principle — except in the case of death. This means that any change affecting the constitutive constraints are changes from one organized situation to another. In our frame, closure is always met, even though the constraints relevant to closure may and do change. The continuous alteration, loss or acquisition of functions result in the realization of new organizational regimes; each regime, in turn, achieves a form of stability determined by closure as a mutual stabilization of constraints. Being subject to both the organization and variation principles, biological organisms realize a succession of different instances of organized regimes over individual and evolutionary times. Then, the stability achieved by the organism is not conservative, but it is for a part cumulative, insofar as it sustains many functional innovations, and makes their preservation over time possible.
Changes of the organization may correspond to several situations depending on the constraints involved. They may be more or less local with respect to the rest of the organization. We propose a typology on this basis:
-
A first situation consists of a local change of a constraint, such that it does not induce a change in the relationship between constraints. For example, a supplementary branching event in a network or tree structure (such as vascular networks or mammary glands) does not correspond to a major reorganization of the constraints of a system. Let us remark, still, that this situation corresponds to a basic symmetry breaking involving the appearance of new relevant quantities of preexisting kinds (for example the angle between the new branches). Therefore, such a change is generic (a branching among many possible branchings). In section 3.1 and 3.3 above, we discussed such examples of generic symmetry changes in the context of specific objects. In turn, the new constraints can be stabilized by generic constraints (insofar as the new branch is stabilized in the same manner than the preexisting ones). In the context of closure, a simple example of a generic stabilization is the inhibition of the proliferation of estrogen-target cells by albumin: after a cell division (which is a symmetry change[19]), the same albumin maintains its inhibitory effect on the new cells.
-
Another situation corresponds to a change involving a modification of the relationship between pre-existing constraints as they come together to generate a new biologically structure or dynamics. Such a change is fundamentally non-local with respect to the graph of interacting constraints. In this kind of situation, some constraints act on processes which they did not constrain before the change. This corresponds typically to the notion of exaptation. In general, such a change implies the alteration or the appearance of specific constraints that establish the new behavior: the important difference with respect to the case described in the previous paragraph is that various other constraints are also mandatory to enable the emergence of the new behavior.
-
Finally, a change in organization might result from the appearance of new constraints. In order for a new constraint to be included in the closed system, the organization must be reshaped so that the new constraint be integrated to the organization (Montévil and Mossio 2015; Mossio, Montévil, and Longo 2016). There are two aspects to this: the new constraint must be maintained by other constraints (I) and maintain another constraint (II). Whether (I) or (II) occurs first corresponds to different scenarios. It is fairly easy to picture a constraint being maintained (criterion I) starting to play a role in an organization after some time (criterion II). For instance, in mammalian development, lungs are first formed and maintained (I) and they acquire a functional role only after birth (II). However, the opposite may also happen, for example, thanks to generic physiological responses discussed above: a change of behavior leading to mechanical friction (II) leads to the strengthening of the skin by keratinization (I). Lastly, the two aspects can be coupled. For instance, some structures (such as muscles, bones, etc.) which are not used (II) may atrophy (I), and reciprocally their use (II) may lead to their further development and strengthening (I).
The key issue about changes of organization is the inscription of the change in a new organization. After a change of constraints takes place at relatively short time scales, the altered constraints involved may be stabilized by other constraints, at longer time scales. These stabilizing constraints are then typically solicited differently than before the change: they maintain, for example, the same tissues but in a different macroscopic shape or configuration. This can happen through generic physiological responses (e.g. keratinization of oral mucosa subjected to friction, resorption of bones under compressive stress, etc.). These changes do not happen only in the interaction with the environment, they happen in essential developmental, metabolic and regulatory processes (as in the developmental processes mentioned above). Another example is given in (David et al. 2013): the authors show that “jamming” the regulation of key metabolic genes of yeast cells did not lead to their death but, instead, to new dynamic behaviors which enabled them to thrive after a transition period.
A change of constraint, or the appearance of a new constraint does not necessarily lead to a stabilization of the new situation. In particular, organized constraints might tend to restore the initial situation because constraints subject to closure are maintained by another constrained process. For example, a mutation in mrna is not going to be sustained because the production of new m rna will not carry the same variation. One might refer to such a tendency as a form of organizational “inertia”. In such a case, the new constraint may vanish at a relatively short time scale. The diametrically opposite situation (among others) is also possible. It corresponds to an amplification of a change affecting a constraint, which in turn destabilizes other constraints in the longer run. It is typically the case in carcinoma where, as stated by the Tissue Field Organization Theory of carcinogenesis, the lack of sufficient constraints on the epithelium can lead to a progressive disorganization of the tissue and, sometimes, disrupt the organization of the whole organism leading to death (Sonnenschein and Soto 2016).
Overall, the principle of variation complements the principle of organization, which should not be conceived as a “fixed point” that iterates itself always identically. Rather, organisms change while staying organized. Variation participates in the robustness of closure in changing environments. Changes of organization actually enabled the maintenance of organisms over very long time scales (during evolution). Last, but not least, current organisms are the product of such variations. Current biological organizations are determined by their (partially) cumulative variations, and this process enables organisms to explore more and more complex organization (Gould 1997; Bailly and Longo 2009; Longo and Montévil 2012; Ana Soto et al. 2016).
5 Non-identical iteration of morphogenetic processes
As a last step, we discuss in this section the connection between the organization and variation principles and the “framing principle” proposed in (Longo et al. 2015), according to which biological phenomena should be understood as “non-identical iterations of morphogenetic processes”. As mentioned in (Mossio, Montévil, and Longo 2016), we submit that organization and variation, taken together, constitute a “organismal specification” of the framing principle. The latter is an informal overarching principle that can be further specified by the two principles of organization and variation.
The framing principle applies to morphogenesis understood in a general sense, that is, both to organogenesis and to proliferation with variation at the cellular level. In other words, both in organ generation (for example, lungs, vascular systems, plants’ organs etc.) and in reproduction, a form is iteratively (and hereditarily) produced, yet never identically. Let us now develop what it means for biological phenomena to be “non-identical iterations of morphogenetic processes”.
By non-identical, we mean (as discussed above) not just quantitative changes but rather unpredictable changes of symmetry, thus unpredictable qualitative changes in the behavior of the object. In the context of the organism, the relevant changes are the ones impacting the organization, that is to say, the ones changing the constraints subject to closure.
The iterations are those of organized objects, subject to closure. However, they should be understood in several ways depending on the particular kind of objects they refer to.
First, closure is by definition about circular causal architectures. For instance, consider a simple closed system, where C1 generates C2 (at time-scale τ1), C2 generates C3 (at time-scale τ2), and C3 generates C1 (at time-scale τ3, say this is the fastest of the three). To discuss iterations, let us consider a perturbation on C1 at t0. This perturbation impacts C2 significantly at time t0 + τ2. Then, C2 impacts C3 at time t0 + τ2 + τ3. Finally C3 impacts C1 at time t0 + τ2 + τ3 + τ1, and this closes the loop.[20] Thus, with the flow time, the circularities of closure lead to iterations of closed patterns. More generally, in a loop described by closure, the duration of the loop as a whole corresponds to the scale of the slowest process. At this time scale, the iterations are the whole set of constrained processes which stabilize and maintain the organization of the organism. Following the principle of variation, these iterations are associated with unpredictable changes of symmetry.
Second, the organizations themselves are iterated. This adds to the principle of organization the notion of reproduction. By reproduction we mean the process of going from one organized object to two (or more) organized objects[21]. Reproduction pertains to the notion that the default state of cells is proliferation (with variation and motility) (Ana Soto et al. 2016; Longo et al. 2015) which complements the principles of organization and variation.
Reproduction is also essential in that organizations which undergo variations may undergo deleterious variations. As a thought experiment, a cell which would never proliferate but would undergo variation should have a finite life expectancy because at some point a deleterious variation would occur. As a result, varying organizations require reproduction to be sustained in an open-ended manner. Reproduction enables a balance between the exploration of possibly morbid variations and the maintenance of a strain of organized systems.
Finally, the framing principle applies also to organ formation. Iteration is a very common morphogenetic process which takes place for example in branching morphogenesis of glands such as the mammary glands, the lungs, etc[22]. Iteration processes explain the abundance of fractal-like structures in biology (Longo and Montévil 2014b). Such multi-scale structures play a particular role because they link different scales, coupling macroscopic and microscopic entities. As such they constitute spatio-temporal coherence structures, which we propose elsewhere to interpret as biological levels of organization (Longo, Montévil, and Pocheville 2012).
6 Conclusions: back to theoretical principles
Biological variation is relevant at all levels of organization, and, for example, it is manifested in the default state of cells (proliferation with variation and motility). The principle of variation that we propose states that biological organisms are specific objects and, thereby, fundamentally different from the objects defined in physical theories. The principle, which draws directly on Darwin’s insights on biological variation, embeds a specific notion of randomness, which corresponds to unpredictable changes of the mathematical structure required to describe biological objects. In this framework, biological objects are inherently variable, historical and contextual. A specific object such as an organism is fundamentally defined by its history and context. Its constraints which may be described by mathematical structures are the result of a history and may change over time.
Our approach to variation contrasts with a relevant part of the theoretical literature on biological organization which aims at investigating the origin of life by the means of minimal or physical models. The strong point of these models is that they lead to tractable mathematics (see for example Luisi 2003; Kepa Ruiz-Mirazo and Moreno 2004). Here, we aim instead at combining organization and variation in a framework that focuses on current organisms, with the massive amount of history that they carry. This difference between the two methodologies corresponds to distinct but complementary aims, and, crucially, to the fact that the concept of organization has been traditionally approached without stressing the importance of variation, its pervasiveness and its conceptual consequences. This has led modeling attempts to focus on generic objects, which are, we think, unable to adequately represent current biological objects.
In order to understand current biological objects, articulating the principle of variation with the principle of organization is necessary. In our framework, organization grounds the relative stability of a set of constraints by the circularity of closure. It controls and counters (a part of the) variation that would be deleterious and would undermine the very existence of the organism. At the same time, organisms undergo quantitative and functional variations, both of them being crucial requirements for their increase in complexity, their adaptability, and, in the end, the sustainability of organization itself as suggested in (K. Ruiz-Mirazo, Peretó, and Moreno 2004). One of the central challenges of a full-fledged theory of organisms consists in providing a coherent account of how they manage simultaneously to restrict and undergo variation.
The epistemological structure of our framework is distinct from the one of physical theories. In physical theories, assumptions on the validity of stable mathematical structures (symmetries) come first, and they may lead to randomness in a given mathematical space. In our framework, variability comes first and closure justifies the validity of constraints.
The notion of constraint is central to our framework. Constraints are the building blocks of mathematical modeling in biology and are the main objects of experimental investigation. The theoretical notion of constraints that we propose should lead to a reinterpretation of mathematical models that are based on them. In our framework constraints depend on the rest of the organism and the rest of the organism depends on them (principle of organization). Moreover, constraints may undergo unpredictable variations (principle of variation).
The principles of variation and organization do not aim at providing a complete framework to understand biological objects (the default state, for instance, is also required), but they elaborate on both the Darwinian and organicist traditions and lead to a significant departure from the physical methodology, which opens the way to original research directions.
Acknowledgments
Maël Montévil’s work is supported by the ‘Who am I’ Labex grant (ANR-11-LABX-0071_WHOAMI). Arnaud Pocheville has been partly supported by Ana Soto’s Blaise Pascal Chair, École Normale Supérieure, Région Île-de-France. The authors are grateful to Cheryl Schaeberle for her linguistic corrections and to Ana Soto for her editorial work.
References
- Bailly, F., and G. Longo. 2009. “Biological Organization and Anti-Entropy.” Journal of Biological Systems 17 (1): 63–96. doi: 10.1142/S0218339009002715.
- ———. 2011. Mathematics and the Natural Sciences; the Physical Singularity of Life. London: Imperial College Press.
- Bailly, F., G. Longo, and M. Montévil. 2011. “A 2-Dimensional Geometry for Biological Time.” Progress in Biophysics and Molecular Biology 106 (3): 474–84. doi: 10.1016/j.pbiomolbio.2011.02.001.
- Barandiaran, Xabier, and Alvaro Moreno. 2008. “Adaptivity: From Metabolism to Behavior.” Adaptive Behavior 16 (5): 325–44.
- Beatty, J. 1995. “The Evolutionary Contingency Thesis.” In Conceptual Issues in Evolutionary Biology., 217. Cambrdige, MA: MIT Press.
- Begley, C. Glenn, and Lee M. Ellis. 2012. “Drug Development: Raise Standards for Preclinical Cancer Research.” Nature 483 (7391): 531–33. doi: 10.1038/483531a.
- Bowler, P. J. 2005. “Variation from Darwin to the Modern Synthesis.” In Variation: A Central Concept in Biology, edited by B. Hallgrímsson and B. K. Hall. Burlington, MA, USA: Elsevier.
- Brisken, Cathrin, Merav Socolovsky, Harvey F. Lodish, and Robert Weinberg. 2002. “The Signaling Domain of the Erythropoietin Receptor Rescues Prolactin Receptor-Mutant Mammary Epithelium.” Proceedings of the National Academy of Sciences 99 (22): 14241–5. doi: 10.1073/pnas.222549599.
- Byers, N. 1999. “E. Noether’s Discovery of the Deep Connection Between Symmetries and Conservation Laws.” In The Heritage of Emmy Noether in Algebra, Geometry, and Physics, 12:67–81. Tel Aviv: Israel mathematical conference.
- Collective. 2005. Variation: A Central Concept in Biology. Edited by B. Hallgrímsson and B. K. Hall. Burlington, MA, USA: Elsevier.
- Danchin, E., and A. Pocheville. 2014. “Inheritance Is Where Physiology Meets Evolution.” The Journal of Physiology 592 (11): 2307–17. doi: 10.1113/jphysiol.2014.272096.
- Darwin, Charles. 1859. On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life. London: John Murray.
- David, Lior, Yossef Ben-Harosh, Elad Stolovicki, Lindsay S. Moore, Michelle Nguyen, Raquel Tamse, Jed Dean, Eugenio Mancera, Lars M. Steinmetz, and Erez Braun. 2013. “Multiple Genomic Changes Associated with Reorganization of Gene Regulation and Adaptation in Yeast.” Molecular Biology and Evolution 30 (7): 1514–26. doi: 10.1093/molbev/mst071.
- De Klerk, GeertJanM. 1979. “Mechanism and Vitalism. A History of the Controversy.” Acta Biotheoretica 28 (1): 1–10. doi: 10.1007/BF00054676.
- Douady, S., and Y. Couder. 1996. “Phyllotaxis as a Dynamical Self Organizing Process Part I: The Spiral Modes Resulting from Time-Periodic Iterations.” Journal of Theoretical Biology 178 (3): 255–73. doi: https://doi.org/dx.doi.org/10.1006/jtbi.1996.0024.
- Dueck, H., J. Eberwine, and J. Kim. 2016. “Variation Is Function: Are Single Cell Differences Functionally Important?” BioEssays 38 (2): 172–80. doi: 10.1002/bies.201500124.
- Eldar, Avigdor, and Michael B Elowitz. 2010. “Functional Roles for Noise in Genetic Circuits.” Nature 467 (7312): 167–73.
- Elowitz, M. B., A. J. Levine, E. D. Siggia, and P. S. Swain. 2002. “Stochastic Gene Expression in a Single Cell.” Science 297 (5584): 1183–6. doi: 10.1126/science.1070919.
- Fox Keller, E. 2005. “Revisiting" Scale-Free" Networks.” BioEssays 27 (10): 1060–8. doi: 10.1002/bies.20294.
- Galton, F. 1894. Natural Inheritance. Macmillan.
- Gilbert, S. F, and D. Epel. 2009. Ecological Developmental Biology: Integrating Epigenetics, Medicine, and Evolution. Sinauer Associates Sunderland.
- Gould, S. J. 1989. Wonderful Life: The Burgess Shale and the Nature of History. New York, USA: Norton.
- ———. 1997. Full House: The Spread of Excellence from Plato to Darwin. Three Rivers Pr.
- Gould, S. J., and E. S. Vrba. 1982. “Exaptation — a Missing Term in the Science of Form.” Paleobiology 8 (1): 4–15.
- Gould, Stephen Jay. 2002. The Structure of Evolutionary Theory. Harvard University Press.
- Griffiths, Paul E, Arnaud Pocheville, Brett Calcott, Karola Stotz, Hyunju Kim, and Rob Knight. 2015. “Measuring Causal Specificity.”
- Karsenti, E. 2008. “Self-Organization in Cell Biology: A Brief History.” Nature Reviews Molecular Cell Biology 9 (3): 255–62. doi: 10.1038/nrm2357.
- Kauffman, S.A. 2002. Investigations. Oxford University Press, USA.
- Kauffman, Stuart A. 2013. “Evolution Beyond Newton, Darwin, and Entailing Law.” Beyond Mechanism: Putting Life Back into Biology, 1.
- Kauffman, Stuart A. 1993. The Origins of Order: Self Organization and Selection in Evolution. Oxford university press.
- Longo, Giuseppe, Catuscia Palamidessi, and Thierry Paul. 2011. “Some Bridging Results and Challenges in Classical, Quantum and Computational Randomness.” In Randomness Through Computation: Some Answers, More Questions, 73–91. World Scientific.
- Longo, G., and M. Montévil. 2011. “From Physics to Biology by Extending Criticality and Symmetry Breakings.” Progress in Biophysics and Molecular Biology 106 (2): 340–47. doi: 10.1016/j.pbiomolbio.2011.03.005.
- ———. 2012. “Randomness Increases Order in Biological Evolution.” In Computation, Physics and Beyond, edited by M. Dinneen, B. Khoussainov, and A. Nies, 7160:289–308. Lecture Notes in Computer Science. Springer Berlin / Heidelberg. doi: 10.1007/978-3-642-27654-5_22.
- ———. 2013. “Extended Criticality, Phase Spaces and Enablement in Biology.” Invited article, special issue. Chaos, Solitons & Fractals, –. doi: 10.1016/j.chaos.2013.03.008.
- ———. 2014a. Perspectives on Organisms: Biological Time, Symmetries and Singularities. Lecture Notes in Morphogenesis. Dordrecht: Springer. doi: 10.1007/978-3-642-35938-5.
- ———. 2014b. “Scaling and Scale Symmetries in Biological Systems.” In Perspectives on Organisms, 23–73. Lecture Notes in Morphogenesis. Springer Berlin Heidelberg. doi: 10.1007/978-3-642-35938-5_2.
- ———. 2014c. “Symmetry and Symmetry Breakings in Physics.” In Perspectives on Organisms, 121–36. Lecture Notes in Morphogenesis. Springer Berlin Heidelberg. doi: 10.1007/978-3-642-35938-5_5.
- ———. n.d. “Comparing Symmetries in Models and Simulations.” In Springer Handbook of Model-Based Science, edited by M. Dorato, L. Magnani, and T. Bertolotti. Springer.
- Longo, G., M. Montévil, and S. Kauffman. 2012. “No Entailing Laws, but Enablement in the Evolution of the Biosphere.” In Genetic and Evolutionary Computation Conference, GECCO’12. New York, NY, USA: GECCO’12; ACM. doi: 10.1145/2330784.2330946.
- Longo, G., M. Montévil, and A. Pocheville. 2012. “From Bottom-up Approaches to Levels of Organization and Extended Critical Transitions.” Frontiers in Physiology 3 (232). doi: 10.3389/fphys.2012.00232.
- Longo, G., M. Montévil, Carlos Sonnenschein, and Ana M Soto. 2015. “In Search of Principles for a Theory of Organisms.” Journal of Biosciences, 1–14. doi: 10.1007/s12038-015-9574-9.
- Lorthois, S., and F. Cassot. 2010. “Fractal Analysis of Vascular Networks: Insights from Morphogenesis.” Journal of Theoretical Biology 262 (4): 614–33. doi: 10.1016/j.jtbi.2009.10.037.
- Luisi, Pier Luigi. 2003. “Autopoiesis: A Review and a Reappraisal.” Naturwissenschaften 90 (2): 49–59.
- Miquel, P.-A., and S.-Y. Hwang. 2016. “From Physical to Biological Individuation.” Progress in Biophysics and Molecular Biology. doi: 10.1016/j.pbiomolbio.2016.07.002.
- Montévil, Maël, Lucia Speroni, Carlos Sonnenschein, and Ana Soto. 2016. “Modeling Mammary Organogenesis from Biological First Principles: Cells and Their Physical Constraints.” Progress in Biophysics and Molecular Biology. doi: 10.1016/j.pbiomolbio.2016.08.004.
- Montévil, M., and Matteo Mossio. 2015. “Biological Organisation as Closure of Constraints.” Journal of Theoretical Biology 372 (0): 179–91. doi: https://doi.org/dx.doi.org/10.1016/j.jtbi.2015.02.029.
- Moreno, A., and M. Mossio. 2015. Biological Autonomy. A Philosophical and Theoretical Enquiry. Dordrecht: Springer.
- Mossio, Matteo, Maël Montévil, and Giuseppe Longo. 2016. “Theoretical Principles for Biology: Organization.” Progress in Biophysics and Molecular Biology. doi: 10.1016/j.pbiomolbio.2016.07.005.
- Mossio, M., C. Saborido, and A. Moreno. 2009. “An Organizational Account of Biological Functions.” The British Journal for the Philosophy of Science 60 (4): 813–41.
- Pocheville, A., and E. Danchin. 2016. “Genetic Assimilation and the Paradox of Blind Variation.” In Challenges to Evolutionary Theory, edited by D.M. Walsh and P. Huneman. Oxford: Oxford University Press.
- Pross, Addy, and Robert Pascal. 2013. “The Origin of Life: What We Know, What We Can Know and What We Will Never Know.” Open Biology 3 (3). doi: 10.1098/rsob.120190.
- Rivenbark, Ashley G, O’ConnorSiobhan M, and William B Coleman. 2013. “Molecular and Cellular Heterogeneity in Breast Cancer.” The American Journal of Pathology 183 (4): 1113–24.
- Ruiz-Mirazo, Kepa, and Alvaro Moreno. 2004. “Basic Autonomy as a Fundamental Step in the Synthesis of Life.” Artificial Life 10 (3): 235–59.
- Ruiz-Mirazo, K., J. Peretó, and A. Moreno. 2004. “A Universal Definition of Life: Autonomy and Open-Ended Evolution.” Origins of Life and Evolution of the Biosphere 34 (3): 323–46. doi: 10.1023/B:ORIG.0000016440.53346.dc.
- Socolovsky, Merav, Isabelle Dusanter-Fourt, and Harvey F. Lodish. 1997. “The Prolactin Receptor and Severely Truncated Erythropoietin Receptors Support Differentiation of Erythroid Progenitors.” Journal of Biological Chemistry 272 (22): 14009–12. doi: 10.1074/jbc.272.22.14009.
- Sonnenschein, Carlos, and Ana Soto. 2016. “Carcinogenesis Explained Within the Context of a Theory of Organisms, Progress in Biophysics and Molecular Biology.” Progress in Biophysics and Molecular Biology. doi: 10.1016/j.pbiomolbio.2016.07.004.
- Sonnenschein, C., and A.M. Soto. 1999. The society of cells: cancer and control of cell proliferation. New York: Springer Verlag.
- Soto, A.M., C. Sonnenschein, and P.-A. Miquel. 2008. “On Physicalism and Downward Causation in Developmental and Cancer Biology.” Acta Biotheoretica 56 (4): 257–74. doi: 10.1007/s10441-008-9052-y.
- Soto, Ana, and Giuseppe Longo. 2016. “Why Do We Need Theories?” Progress in Biophysics and Molecular Biology. doi: 10.1016/j.pbiomolbio.2016.06.005.
- Soto, Ana, Giuseppe Longo, Maël Montévil, and Carlos Sonnenschein. 2016. “The Biological Default State of Cell Proliferation with Variation and Motility, a Fundamental Principle for a Theory of Organisms.” Progress in Biophysics and Molecular Biology. doi: 10.1016/j.pbiomolbio.2016.06.006.
- Soto, Ana M., and Carlos Sonnenschein. 2005. “Emergentism as a Default: Cancer as a Problem of Tissue Organization.” Journal of Biosciences 30 (1): 103–18. doi: 10.1007/BF02705155.
- Stoer, Josef, and Roland Bulirsch. 2013. Introduction to Numerical Analysis. Vol. 12. Springer Science & Business Media.
- Thomas-Vaslin, Véronique, Adrien Six, Bertrand Bellier, and David Klatzmann. 2013. “Encyclopedia of Systems Biology.” In, edited by Werner Dubitzky, Olaf Wolkenhauer, Kwang-Hyun Cho, and Hiroki Yokota, 1149–52. New York, NY: Springer New York. doi: 10.1007/978-1-4419-9863-7_96.
- Turing, A. M. 1952. “The Chemical Basis of Morphogenesis.” Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 237 (641): 37–72. doi: 10.1098/rstb.1952.0012.
- Van Fraassen, B.C. 1989. Laws and Symmetry. Oxford University Press, USA.
- Varela, F.G., H.R. Maturana, and R. Uribe. 1974. “Autopoiesis: The Organization of Living Systems, Its Characterization and a Model.” Biosystems 5 (4): 187–96. doi: 10.1016/0303-2647(74)90031-8.
- Vogel, David, Stamatios C. Nicolis, Alfonso Perez-Escudero, Vidyanand Nanjundiah, David J. T. Sumpter, and Audrey Dussutour. 2015. “Phenotypic Variability in Unicellular Organisms: From Calcium Signalling to Social Behaviour.” Proceedings of the Royal Society of London B: Biological Sciences 282 (1819). doi: 10.1098/rspb.2015.2322.
- West, B.J. 2006. Where Medicine Went Wrong: Rediscovering the Path to Complexity. Vol. Volume 11 of Studies of nonlinear phenomena in life sciences. Teaneck, NJ: World Scientific.
- West, G.B., and J.H. Brown. 2005. “The Origin of Allometric Scaling Laws in Biology from Genomes to Ecosystems: Towards a Quantitative Unifying Theory of Biological Structure and Organization.” Journal of Experimental Biology 208 (9): 1575–92. doi: 10.1242/jeb.01589.
- West-Eberhard, Mary Jane. 2003. Developmental Plasticity and Evolution. Oxford University Press.
- Yamada, Takuji, and Peer Bork. 2009. “Evolution of Biomolecular Networks—Lessons from Metabolic and Protein Interactions.” Nature Reviews Molecular Cell Biology 10 (11): 791–803. doi: 10.1038/nrm2787.