Géométrie du temps biologique : Rythmes et protension
Questions de phrasé
Nous distinguons les rythmes de type physique de ceux proprement biologiques. Nous abordons aussi les activités protensives et rétensives du vivant.
Abstract
Le vivant possède une phénoménalité particulière et originale. Comme cadre et siège de cette phénoménalité, l’organisation temporelle des organismes est elle-même d’une grande richesse. Ainsi, l’on rencontre dans l’activité biologique des cas de cyclicité : cycle cardiaque, cycle respiratoire, rythmes cérébraux, cycles circadiens, cycle de vie, etc. ; et d’autre part il s’y présente, parfois même au sein de ces cycles, des phénomènes dont la nature semble plutôt être caractérisée par une irréversibilité fondamentale : cognition, nutrition, développement, vieillissement, évolution, ...Il nous semble dès lors impératif, pour aborder théoriquement — et donc aussi empiriquement — ces phénomènes, de les considérer dans un cadre où la question de la temporalité soit abordée de manière adéquate.
Table of contents
Reading time: ~64 min
Géométrie du temps biologique : rythmes et protension
1 Introduction
Le vivant possède une phénoménalité particulière et originale. Comme cadre et siège de cette phénoménalité, l’organisation temporelle des organismes est elle-même d’une grande richesse. Ainsi, l’on rencontre dans l’activité biologique des cas de cyclicité : cycle cardiaque, cycle respiratoire, rythmes cérébraux, cycles circadiens, cycle de vie, etc.; et d’autre part il s’y présente, parfois même au sein de ces cycles, des phénomènes dont la nature semble plutôt être caractérisée par une irréversibilité fondamentale : cognition, nutrition, développement, vieillissement, évolution, ...Il nous semble dès lors impératif, pour aborder théoriquement — et donc aussi empiriquement — ces phénomènes, de les considérer dans un cadre où la question de la temporalité soit abordée de manière adéquate.
Nous proposons dans ce texte de décrire deux directions que nous avons explorées en ce sens Bailly, Longo et Montévil 2011; Longo et Montévil 2011. L’idée au cœur de ces propositions est d’aborder les phénomènes vivants en s’inspirant des démarches théoriques employées en science physique. Le premier principe de cette démarche consiste, à notre sens, à s’appuyer sur les particularités et les régularités — et irrégularités — des phénomènes que l’on se propose d’étudier pour concevoir des cadres théoriques originaux, et souvent contre-intuitif, à même de tenir compte de ces phénoménalités. Ce faisant, la physique s’est développée autour d’une certaine audace et radicalité dans la formulation de cadres théoriques alternatifs.
Ainsi, pour ce qu’il est des conceptions ayant trait à la temporalité, les physiciens ont d’abord proposé (et constitué en collaboration avec les mathématiciens) le temps comme droite continue, modélisée mathématiquement par le continu cantorien en temps qu’objet et par le calcul différentiel comme procédure pour déterminer les trajectoires dans l’espace, trajectoires paramétrées par le temps et pour lesquels une certaine grandeur, l’énergie, est conservée (lorsque le système est isolé, les autres situation s’en déduisant). La relativité (restreinte ou générale) a rendu cette approche plus complexe en abordant la question du temps comme formant un “bloc” avec l’espace, conférant alors à temps et espace une quasi symétrie conceptuel et mathématique. Notons que ce cadre conduit notamment à la mise en difficulté de l’intuition courante, car la notion de simultanéité y est relative (deux phénomènes ne peuvent être considérés comme simultanés que relativement à un référentiel et ne le seront pas forcément dans un autre). La physique quantique, au contraire, maintient pour le temps un statut de paramètre, comme paramètre des transformations des états quantiques (entre deux mesures). La mesure cependant ajoute un second aspect temporel à ce cadre, sans durée, mais décrivant un avant et un après, caractérisé par la disparition d’une partie de l’état antérieur et donc une situation fortement irréversible. La physique quantique a été aussi le cadre de proposition théoriques plus audacieuses, tel que le temps imaginaire (au sens des complexes) utilisé par Hawking pour faire disparaître certaines singularités, notamment dans l’étude du big bang. Un autre exemple intéressant est celui de la symétrie (charge, parité, temps, fondamentale en physique des particules), qui lors de la création d’antimatière, est “menacée” par la brisure de la symétrie de charge alors que la parité est conservée. Feynmann considéra dès lors que le temps pouvait s’inverser localement, donnant au parcours temporel une structure en zig-zag et conservant ainsi la symétrie , voir Feynman et al. 1980. Ainsi, ces exemples, très divers, montrent comment la réorganisation théorique de l’appréhension des structures temporelles permet l’intelligibilité des phénomènes.
Les organismes vivant, eux, se présentent comme des organisateurs du temps. Ainsi si certains aspects du temps de la physique classique restent valides — il est toujours possible de mesurer à l’aide d’une horloge l’instant auquel tel ou tel événement se produit ou la durée de tel ou tel phénomène, voir section 2 —, un certain nombre de situations conduisent à d’autres propositions, mettant en avant l’unité organisationnelle qui existe entre une souris et un éléphant par exemple McMahon 1980; West et Brown 2005. D’autres approches consiste à étudier à l’aide de systèmes dynamiques classiques comment tel ou telle structure temporelle peuvent apparaître, Winfree 2001. Nous pensons cependant que ces approches ne permettent pas de tenir compte de l’originalité phénoménale du vivant, laissant de coté le rôle du temps physique dans le premier cas, et ne prenant pas en compte l’autonomisation du temps biologique vis à vis du temps physique dans le contexte d’un organisme pour le second.
Ces critiques poussent à une conceptualisation originale du rapport entre temps physique et temps biologique qui peut être exprimée en terme de “phrasé”. Ainsi le temps biologique peut être analysé comme phrasé par rapport au temps physique, il n’est pas un temps fondamentalement incompatible avec le temps physique, et l’on peut voir des régularités moyennes dans leurs rapports. Cependant la constitution du temps biologique se fait, à notre avis, dans le cadre de la criticité étendue (voir Bailly et Longo 2011, 2008a; Longo et Montévil 2011) où les symétries donnant en particulier les trajectoires spécifiques des systèmes dynamiques (et in fine la validité de leurs attracteurs) se trouvent brisées. Ainsi, il y a une forme d’irrégularité ou d’incommensurabilité, à notre sens, entre le temps physique et le temps biologique en tant que ce dernier n’est pas “arrimé” au temps physique par les symétries que les systèmes physiques usuels possèdent. Ce décalage n’est pas dû, à notre sens, à l’adjonction de quelque propriété extérieure au monde physique, mais aux singularités que nous proposons comme présentes au cœur de la détermination biologique. Pour donner un exemple particulièrement concret, considérons la question de la détermination du rythme cardiaque. La plupart des approches présentes dans la littérature proposent d’aborder le cœur ou les systèmes neuronaux de régulation cardiaques comme des systèmes dynamiques; cette approche pose cependant des problèmes théoriques majeurs. D’une part elles laissent de coté les relations d’allométries, voir section 2.1, et de l’autre elle laisse de coté le fait qu’il n’y a pas de situation biologique où l’activité cardiaque n’est pas liée causalement à l’activité de l’organisme (et des différents autres organes) et à son histoire, que cela soit au temps courts ou longs,...L’étude de la dynamique des parties de l’organisme que sont le cœur ou son système de régulation n’est cependant pas dénuée de sens et ces aspects mécaniques et électro-physiologiques jouent un rôle crucial...mais la question du régime causal pertinent reste, à notre sens, ouverte.
C’est donc cet écart entre temps biologique et temps physique que nous proposons de lire comme phrasé. Nous allons expliciter dans la première section de ce texte une proposition théorique permettant, par une approche géométrique, de considérer à la fois l’autonomie du temps biologique et son rapport à certains aspects du temps physique. Cette approche nous permettra aussi d’appréhender en une représentation synthétique la structure fine du rapport entre rythmes biologiques (avec l’exemple du rythme cardiaque) et temps physique, cette structure dépendant notamment de l’état de santé de l’organisme considéré. Dans la second partie, nous décrirons un autre aspect du temps biologique, que nous aborderons comme la tension mise en place par l’organisme entre événements passés et événements futurs et virtuels, ceci constituant dès lors un autre aspect de la réorganisation du temps dans les systèmes biologiques.
2 Une approche géométrique des rythmes biologiques
Dans cette section, nous décrirons notre approche des rythmes biologiques, développée dans Bailly, Longo et Montévil 2011. Il s’agira ici de proposer un cadre relativement simple où l’organisation temporelle des phénomènes biologiques nous amènera à proposer l’introduction d’une dimension temporelle supplémentaire. Ce cadre, nous le verrons, permet de considérer ensemble des invariants biologiques moyens de nature différentes. De plus, il permet de mettre en évidence la structure de la variabilité de certains rythmes biologiques pour une trajectoire expérimentalement mesurée.
2.1 Deux types de rythmes
Pour aborder l’organisation du temps biologique, il convient d’organiser les situations rythmiques suivant leurs propriétés d’invariance. Cette approche nous conduit alors à distinguer deux cas de rythmicité dont la nature est profondément différente :
| , en min. | exposant | |
|
Durée de vie en captivité |
6.8 | 0.20 |
|
98% de la croissance |
5.8 | 0.26 |
|
Temps de doublement de la population |
5.5 | 0.26 |
|
Temps pour atteindre la maturité reproductive |
5.5 | 0.18 |
|
50% de la croissance |
5.3 | 0.25 |
|
Temps de gestation |
5.0 | 0.25 |
|
Temps pour métaboliser les réserves de graisse (0.1% de la masse corporelle) |
2.2 | 0.26 |
|
Temps de demi-vie d’un médicament (methotrexate) |
1.8 | 0.19 |
|
Clairance du plasma, inulin |
0.8 | 0.27 |
|
Temps de circulation du sang |
-0.5 | 0.21 |
|
Durée des battements intestinaux |
-1.3 | 0.31 |
|
Cycle respiratoire |
-1.7 | 0.26 |
|
Cycle cardiaque |
-2.4 | 0.25 |
|
Temps de contraction élémentaire, soleus |
-3.0 | 0.39 |
|
Temps de contraction élémentaire, extensor digitorum longus |
-3.5 | 0.21 |
- (Ext)
- les rythmes “externes”, sont déterminés d’abord par un phénomène extérieur à la détermination proprement biologique. Il en résulte que leurs propriétés temporelles ont généralement pour invariant une quantité dimensionnelle (de dimension, un temps) et correspondant à la période de ce rythme. Ce type de rythmes est généralement associé à une description par décomposition spectrale comme somme d’harmonique et sous harmoniques (en ). L’exemple paradigmatique de ce type de rythmes est le rythme circadien, mais d’autre rythmes importent, tels que les rythmes circannuels, ou le rythmes des marées pour certains organismes. Notons que le caractère extérieur de la détermination de ces rythmes est transparent dans leur appellation puisque leur étymologie provient du latin circa signifiant autour. Ces rythmes ont comme origine de leurs propriétés (période et phase notamment) des situations pour lesquelles l’approche théorique se fait dans un cadre purement physique (mécanique et gravitation pour les exemples sus-cités). Il en résulte que ces propriétés ne dépendent pas de l’organisme considéré. Notons que si ces caractéristiques sont invariantes pour un rythme donné, leur impact sur une espèce ou un organisme précis est plus complexe. En effet, le rythme circadien, par exemple, est le même pour tous les organismes (en fonction de leur position sur le globe terrestre) mais les organismes diurnes et nocturnes aurons des phases d’activité décalées (avec cependant la même phase pour le rythme physique). De plus, de très nombreux organismes (sinon tous) ont une ou plusieurs horloges internes, qui suivent ces rythmes et qu’ils maintiennent synchronisées grâce à des indices tels que la luminosité.
- (Int)
- les rythmes “internes”, au contraire, dépendent en particulier de la masse adulte de l’organisme considéré. Ils ont comme propriété, en générale, d’avoir une vitesse par rapport au temps physique (mesuré grâce à un chronomètre) qui soit proportionnel à la masse adulte de l’organisme à la puissance , voir Lindstedt et Calder III 1981; Schmidt-Nielsen 1984; Savage et al. 2004). Des exemples sont donnés dans la table 1. Notons en particulier que les rythmes cardiaques, respiratoires et (approximativement) l’espérance de vie suivent ce genre d’invariants. Il en résulte que l’invariance qui apparaît alors n’est pas d’abord dans le lien avec le temps physique, mais dans le rapport entre ces rythmicités, ce rapport servant à décrire le nombre d’itérations d’un rythme pendant une itération d’un second rythme. Ce nombre est alors indépendant de la masse de l’organisme considéré — ainsi apparaît notamment le nombre total d’itérations du cycle cardiaque au cours de la vie d’un organisme, comme indépendant de l’organisme considéré, du moins parmi de grandes classes d’organismes telle que celle des mammifères. Notons de plus que la vitesse de ces rythmes peut varier en fonction du niveau d’activité de l’organisme considéré.
| tempo | description | pulsations/min | niveau d’activité | équivalent en masse |
| chez l’homme | ( en kg) | |||
| Largo | Large (lent) | 40 – 60 | sommeil | 660 – 129 |
| Lento | Lent | 52 – 68 | 230 – 78 | |
| Adagio | À l’aise | 60 – 80 | veille (au repos) | 130 – 41 |
| Andante | Modéré (allant) | 76 – 100 | 50 – 16 | |
| Moderato | Modéré | 88 – 112 | 50 – 11 | |
| Allegretto | animé | 100 – 128 | 16 – 6.3 | |
| Allegro | Gai, vif, allègre | 112 – 160 | aérobique | 11 – 2.5 |
| Vivace | Vif | 140 | 4.4 | |
| Presto | Rapide | 140 – 200 | anaérobique | 4.4 – 1 |
| Prestissimo | Très rapide | 190 | maximum | 1.3 |
Partant de cette distinction, nous proposons d’associer aux rythmes externes la dimension usuelle du temps physique, , représentée par une droite, et qui est le support habituel de ce type d’invariants. En revanche, nous proposons d’ajouter une dimension temporelle supplémentaire associée au rythmes internes, , dont la topologie est celle d’un cercle[1], et à laquelle est associée un nombre d’itérations . Notons que l’intérêt de cette proposition n’est pas uniquement dans l’adéquation aux invariants (approchés) rencontrés dans les phénomènes mentionnés, elle permet de plus d’engendrer un degrés de liberté supplémentaire dans la description de la temporalité de ces phénomènes. Ainsi, nous avons vu que le temps entre deux itérations d’un rythme interne varie comme pour des adultes étant dans un niveau d’activité modérée, mais de plus cette période change, bien évidemment, lorsque le niveau d’activité varie. Dès lors, des vitesses différentes pour un rythme donné peuvent être interprétées de deux manières différentes. Nous avons illustré ce fait dans le tableau 2, en mettant en correspondance les tempo musicaux avec le rythme cardiaque : d’une part à différents niveaux d’activité chez l’homme et d’autre part en envisageant une correspondance avec des animaux au même niveau d’activité mais ayant différentes masses adultes, illustrant ainsi la notion d’allométrie.

Décrivons dans un premier temps qualitativement la structure géométrique que nous proposons pour le temps biologique, voir figure 1. Précisons tout d’abord que nous limiterons à considérer un rythme interne. Étant bidimensionnelle, cette structure se présente comme une surface, qu’il convient dès lors de décrire dans un espace de plongement de dimension trois. Un organisme a une origine temporelle (que l’on peut choisir en général comme le moment de la naissance, ou le moment de la mise en place du rythme que l’on considère), puis progresse dans son temps propre, d’abord rapidement lors du développement, puis à une vitesse plus lente. Notons que ce langage informel sera objectivé et articulé à l’empirie par notre approche quantitative de ce schème. Maintenant, envisageons un rythme externe, tel que le rythme circadien. Ce rythme impacte l’activité biologique en tant qu’il la ralentit et l’accélère périodiquement (au sens du temps physique). Nous proposons dès lors de considérer que ce rythme engendrera une spirale tournant autour de la courbe décrivant le rythme moyen de vieillissement. Ainsi, nous obtenons une spirale d’axe courbe (à peu près droit chez l’adulte). Finalement, le rythme interne constituera lui même une seconde spirale, prenant comme axe la première et qui engendrera une structure tubulaire, caractérisant l’autonomie de ce rythme vis à vis du temps physique.
2.2 Une mathématisation de ce schème
2.2.1 Cadre mathématique
Comme référentiel de base nous choisissons des coordonnées cartésiennes orthogonales. Les axes et sont orientés de manière usuelle ( vers la droite et vers le haut). On propose d’interpréter l’abscisse comme correspondant au temps physique objectif, orienté comme tout temps thermodynamique et qui permet la caractérisation des instants et la mesure des durées. correspond à l’avancée dans le temps biologique propre, ceci acquérant un sens précis grâce à notre modèle. Enfin, et puisque notre espace de plongement est tridimensionnel, nous disposons d’un troisième axe, , imposé pour des raisons mathématiques et dont le sens sera précisé ultérieurement.
Nous proposons maintenant un squelette mathématique pour représenter ce temps biologique :
-
La progression moyenne dans la direction
sera représentée par une fonction
.
est une fonction croissante, à cause de l’irréversibilité du temps biologique et a une dérivée décroissante à cause du ralentissement de l’activité
biologique lors du développement et du vieillissement.
correspond à l’instant physique d’un événement biologique de référence marquant l’origine du temps biologique (l’instant de la fécondation, par exemple).
est le temps caractéristique, dépendant surtout de la masse adulte, d’un rythme biologique interne choisit arbitrairement pour servir de référence (la période moyenne du rythme cardiaque, respiratoire,...). Cette quantité
représente “l’âge propre” du système biologique considéré. Dans le réferentiel
, nous posons donc :
Figure 2: Illustration qualitative des premières composantes de notre modè le gauche , la fonction , représentant l’age global de l’organisme : cet age augmente plus vite durant le développement puis son augmentation ralenti ensuite progressivement. En orange un petit mammifère (une souris par exemple) et en rouge un organisme plus gros (un éléphant par exemple). La durée de vie du premier est plus petite que celle du second. droite , En bleu et jaune un rythme physique a été ajouté. Remarquons que ce rythme est le même pour les deux organismes considérés, une période correspond alors à une plus grande partie du temps de vie du temps de vie l’organisme de petite taille que de celle de l’organisme plus gros. (1) -
Nous considérons maintenant un rythme biologique externe, de période
(et donc de pulsation
), ayant des effets sur l’activité biologique. Le rythme circadien par exemple conduit à
heures.
Dans la définition de , correspond à l’impact du rythme physique sur le rythme biologique, indépendamment de la masse de l’organisme considéré :
(2) En effet le terme est proportionnel au nombre d’itérations du temps compacifié pendant une période du temps physique. Ce terme permet alors de comprendre qu’un jour ou une année, par exemple, a un poids bien plus important pour une souris qu’un éléphant.
-
Nous pouvons enfin ajouter un rythme proprement biologique, dépendant d’une fonction
. Cette fonction a un sens biologique : si nous convenons que
alors
est le nombre d’itérations du rythme biologique considéré à l’instant
. Remarquons que ce sens biologique provient directement du fait que le temps biologique ainsi considéré a une origine (un minimum), ce qui
correspond à une situation inverse des situations physiques, les temps physiques (classiques, relativistes et quantiques) étant invariants par translation. Ce point est particulièrement important car le théorème de Noether montre
que cette symétrie du temps physique, dans le cadre classique, correspond à la conservation de l’énergie, et permet ultimement la détermination des trajectoires. De manière similaire, dans le cadre quantique, temps et énergie sont
conjugués mais leurs statuts n’est pas symétrique car le théorème de Pauli montre que la borne inférieure pour l’énergie (une absence de symétrie par translation) est incompatible avec l’existence d’un opérateur temps, voir Bailly,
Gaill et Mosseri 1993; Longo et Montévil 2011.
(3)
Nous proposons ensuite de considérer que est déterminé (en moyenne) par les propriétés métriques de , modulo une hypothèse supplémentaire sur l’effet du temps physique sur le temps biologique en dehors de toute activité biologique (on peut penser à la congélation, voir Bailly, Longo et Montévil 2011), nous obtenons :
| (4) |
Nous pouvons maintenant proposer une interprétation de l’axe . En effet, à cet axe correspond le choix arbitraire du sens de rotation de l’hélice correspondant au rythme physique. Résultant de ce choix, une direction de l’axe correspondra à une accélération du temps biologique alors que l’autre direction correspond à un ralentissement, voir figure 2.
Nous considérons de plus que la vitesse de rotation en fonction du temps compacifié est constante ce qui conduit à un rayon .
| (5) |
Ce cadre permet alors de lier les propriétés du temps bidimensionnel avec des quantités observables, et conduit à un certain nombre de prédictions, détaillées dans Bailly, Longo et Montévil 2011. Plus précisément, les itérations observables du temps compacifié (battements de cœur, respirations,...), repérées par le temps physique, déterminent directement , et permettent donc d’estimer les autres fonctions présentes dans notre schème. Les prédictions qui s’ensuivent concernent essentiellement l’impact d’un rythme externe sur un rythme interne, cet impact étant quantitativement différent lorsque l’on compare des organismes adultes de masses différentes et un organisme lors de son ontogenèse (où un vaste ensemble de masses est aussi parcouru, mais conduit à des conséquences différentes).
Nous allons maintenant nous focaliser sur ce que ce cadre permet, lorsque nous considérons la structure fine de la variabilité des rythmes biologiques (et non plus des moyennes).
2.3 Variabilité des rythmes internes

Pour aborder la variabilité d’un rythme interne (et par la suite nous nous focaliserons sur le rythme cardiaque), nous considérons la dérivée de par rapport à :
| (6) |
Nous obtenons alors la fréquence instantanée du rythme considéré,
, comme rayon de la composante associée au temps compacifié, (cette composante a cette fois la dimensionnalité d’une fréquence).
Pour appréhender la structure temporelle d’un rythme biologique nous proposons de plus une procédure de “renormalisation”, consistant à regrouper
itérations du temps compacifié passant ainsi d’un temps
à un temps
. En utilisant le principe de la vitesse constante du temps compacifié on obtient
.
(a) Une vue globale (2
jours).
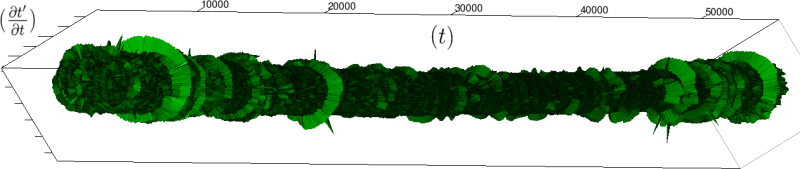 (b) Nuit, groupes de 200 battements
(b) Nuit, groupes de 200 battements
 (c) Jour, groupes de 200 battements
(c) Jour, groupes de 200 battements
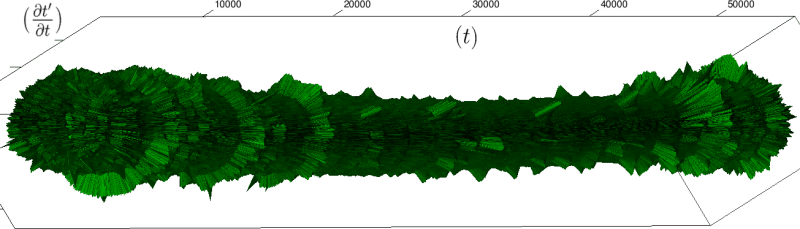 (d) Nuit, groupes de 600 battements
(d) Nuit, groupes de 600 battements
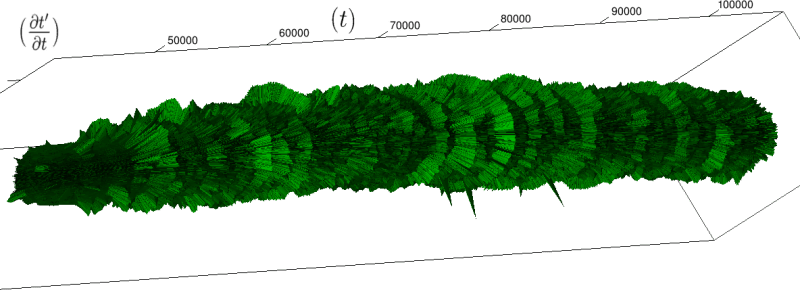
(e) Jour, groupes de 600 battements

Nous pouvons alors injecter directement des données expérimentales dans notre cadre géométrique (essentiellement des séries temporelles d’intervalles entre battements de cœur). Nous obtenons alors une visualisation originale, voir figure 4, de phénomènes déjà observés par ailleurs, voir par exemple Gang et Malik 2003; Malik et al. 1996; Massin et al. 2000. Plus précisément, le rythme cardiaque (contrairement à l’intuition usuelle) n’est pas régulé autour d’une valeur fixe (avec quelque fluctuations aléatoires) mais au contraire, il fait preuve, pour un organisme en bonne santé et en état de veille, de fluctuations à toutes les échelles, lui donnant alors une structure fractale. Dans notre cadre, cette structure apparaît très clairement par la présence, en des positions irrégulières, d’excroissances circulaires (correspondant à une accélération cardiaque pendant un nombre de battements au moins aussi grand que l’échelle de renormalisation; cette échelle est, rappelons-le, nombre de battements nécessaires pour faire un tour complet du cylindre). Lors du sommeil, au contraire, le rythme cardiaque est régulier (cylindre lisse) avec quelque pics d’activité de longueur fixe (portions de cercle de taille régulière devenant de plus en plus petites lorsque l’on accroît l’échelle de renormalisation).
De plus cette structure de l’activité cardiaque est caractéristique d’une personne en bonne santé et a donc des applications en terme de diagnostique médical (généralement abordées par l’analyse en ondelette). Notre cadre permet dès lors de voir comment cette structure change suivant les cas, et en particulier pour différentes situations pathologiques, voir figure 5. Les différences entre cas apparaissent alors alors à travers une structure spatialisée synthétique et facilement interprétable : le cas d’une régulation artificielle du rythme cardiaque donne une structure lisse, le cas de fibrillation auriculaire (une forme d’arythmie) donne une structure “poilue”, caractéristique de l’irrégularité très forte de l’activité cardiaque aux temps courts, et le dernier cas, dont la série aboutit à une mort cardiaque subite, présente une régularité anormale du rythme cardiaque (structure relativement lisse).
2.4 Conclusion : des rythmes à la protension
Nous avons vu que l’exploitation des invariants moyens dont nous disposons nous permet de proposer une dimension supplémentaire pour le temps biologique. Cette dimension caractérise l’autonomisation du temps biologique vis à vis du temps physique. Cette autonomie permet dès lors la mise en place d’une structure propre, caractérisée par la variabilité de ce temps biologique vis à vis du temps physique, structure que l’on peut lire comme phrasé en tant qu’elle est variation basée sur une invariance sous-jacente, et qu’elle peut avoir des formes différente suivant les cas, qu’il s’agisse de pathologies ou de changement de niveau d’activité.
On peut, toujours dans ce cadre, considérer des aspects supplémentaires de la constitution du temps biologique en lien avec le temps physique. Ainsi, considérons , une progression infinitésimale du temps biologique global. est relié à l’élément de temps physique et à l’élément de temps biologique “pur” par la relation évidente ; on peut dès lors écrire comme - ou encore
On peut alors interpréter le premier terme comme élément infinitésimal de rétention (il est constitué d’un recule infinitésimal du temps globale de l’organisme par l’effet du temps physique). Le second terme, au contraire, est un prolongement du temps de l’organisme par l’élément infinitésimal de temps physique, ainsi il peut donc être interprété comme un élément de protension. Nous allons dans la seconde partie de ce texte formuler une approche visant à objectiver de manière indépendante ces concepts de protension et de rétention.
3 Rétention et protension en biologie
Dans cette section, nous décrirons l’analyse de la protension et de la rétention en biologie que nous avons développée dans Longo et Montévil 2011. Il s’agit d’aborder théoriquement la constitution par les objets biologique d’un présent étendu, conceptualisé comme tension locale entre un passé et un futur proche. Ainsi, en tant qu’organisateurs de leurs temporalités, les êtres vivants ne se contentent pas de “réagir” aux événements, mais les maintiennent et les prolongent, constituant ainsi une forme originale de présent, étendu, que nous essayons de contribuer à décrire.
3.1 Préliminaires théoriques
Il convient d’abord de préciser en quel sens nous parlons de protension et de rétention. Ces termes proviennent de la phénoménologie et en particulier de la philosophie husserlienne. Rappelons que la phénoménologie peut être définie de manière concise comme l’étude de ce qui apparaît à la conscience et plus précisément l’étude des modalités d’apparition des phénomènes conscients. Par cette méthode, Husserl distingue la mémoire comme reconstruction d’un passé distant, de la rétention, consubstantielle à l’appréhension des phénomènes et à la constitution du présent. De même, l’anticipation est la conscience d’une attente et d’un futur possible alors que la protension est dans le présent sa tension vers l’avenir immédiat.
Ces distinctions se retrouvent en biologie, notamment à travers le projet visant à naturaliser la phénoménologie Van Gelder 1999. Ainsi, Edelmann comprend la mémoire en termes neurologiques comme “cerveau qui se remet dans un état vécu” Edelman et Tononi 2000, 2001, alors que Varela 1999 s’intéresse à la constitution chez le vivant d’un specious present, un présent étendu par comparaison avec le présent ponctue,l “instantané”, en physique classique.
Notre approche sera cependant différente puisque nous visons à appliquer ces concepts dans un cadre biologique général, y compris donc à des organismes unicellulaires. Nous proposons d’aborder la protension et la rétention en utilisant la notion de temps caractéristique. Celle-ci nous permettra de formuler un squelette mathématique, rudimentaire mais précis, qui, nous l’espérons, permettra de clarifier ces notions.
Rappelons que notre cadre conceptuel est celui de la criticité étendue Bailly et Longo 2011, 2008a; Longo et Montévil 2011, or il est intéressant de mentionner le fait que la criticité physique est généralement accompagnée d’un phénomène de ralentissement critique Suzuki, Kaneko et Takesue 1982 : le temps de relaxation (de retour à l’équilibre après une perturbation) d’un système temps vers l’infini lorsqu’on approche ce système d’un point critique. Le sens qualitatif de ce type de situation, en biologie, serait que le système sous l’effet d’un stimulus prendrait un temps extrêmement long à se stabiliser à nouveau (ou plus généralement, l’organisme prendrait un temps important pour réagir ou s’adapter). Ainsi donc, si l’organisme est compris comme étant en permanence en une situation de criticité, il aurait des temps de réaction très lents si on considère qu’une réaction adaptée nécessite une stabilisation. Plus généralement, et y compris dans le cadre d’une approche en termes de théorie de l’information, le temps d’élaboration/réaction est nécessairement grand pour un organisme ayant de grandes longueurs de corrélation et des composants ayant des temps caractéristiques grands (donc des réponses lentes). Pourtant, l’on observe qu’en général les organismes sont capables de réactions rapides, et donc que l’organisation biologique doit fournir une solution à ce paradoxe. Nous proposons d’appréhender cette solution — ou tout au moins une partie de cette solution — en disant que l’organisme compense cette lenteur en se préparant en avance à l’arrivée d’un stimulus (que cela soit au niveau de la détection du stimulus à proprement parler ou au niveau de la réaction elle-même). Ainsi, la protension apparaît comme une forme de lenteur négative, un prolongement virtuel du passé, servant de support à la réaction à un futur proche et aux changements d’activité physiologique que cette réaction nécessite. Conceptuellement il est alors aussi logique que cette forme d’organisation conduise à une notion spécifique d’inertie biologique, constituée par ces prolongements protensifs. Notons que cette justification théorique correspond, de fait, à un grand nombre de comportements observés expérimentalement, voir par exemple Berthoz 1997 et la discussion 3.5.
3.2 Principes
Nous avons présenté les notions de protension et de rétention comme maintient élémentaire du passé et prolongement/estimation élémentaire du future. Ces composantes sont le résultat de l’activité biologique en tant que constituée par un organisme, par-delà les structures temporelles usuelles en physique, mais relèvent aussi, de part leurs caractère élémentaire et “local” dans le temps, d’une certaine “passivité” si l’on compare ces notions aux situations de mémoire et d’anticipation, participant en générale d’une attention, et pour lesquels protension et rétention se présentent comme étant en amont. Une autre manière de considérer cet aspect est de dire que lors de la protension et de la rétention, si la globalité de l’organisme peut être impliquée, elle ne l’est que faiblement (sans résonances complexes entre les niveaux d’organisations), alors que ces phénomènes ne sont pas particulièrement contraints dans la mémoire et l’anticipation. Partant, ces notions ne nécessitent en aucun cas la mise en places d’un système nerveux complexe et peuvent s’appliquer notamment aux unicellulaires.
Formalisons maintenant quelque peu ces notions. Nous décrirons tout d’abord la rétention
:
à un instant
pour un “événement”
de nature
, antérieur, pour lequel on posera
(où
).
est la protension virtuelle, d’un événement de même nature au moment pour un instant postérieur ( ). Nous proposons de considérer de manière principielle que la protension virtuelle ne peut avoir lieu que s’il y a une rétention correspondant à un événement de même nature. La protension virtuelle sera donc considérée comme fonction de la rétention et on aura pour . Pour la même raison, on posera que cette protension est une fonction croissante de la rétention en question, soit . Nous faisons dès lors correspondre ces quantités à l’analyse phénoménologique de la protension et de la rétention lorsqu’elle est possible, notre approche permettant un élargissement de l’application de ces notions ainsi que leurs stabilisation par l’usage de mathématiques élémentaires.
3.3 Spécifications
Pour aller plus loin dans cette étude, nous proposons une formulation explicite de la rétention et de la protension virtuelle. Ceci nous permettra, par des manipulations mathématiques élémentaires, de jouer sur les concepts dont nous voulons approfondir la signification et les reformulations possibles. La formulation que nous proposons utilise la notion, extrêmement classique en physique, de de fonction de relaxation[2].
Nous proposons d’utiliser des fonctions de relaxation, car la diminution progressive de la rétention, en s’éloignant dans le temps du début d’une phrase, voire, de manière plus générale, de toute action (y compris l’écoute), peut être considérée comme une sorte de “retour à l’équilibre”. Un retour nécessaire si on veut saisir le sens de la phrase ou passer à une autre action. Bien entendu, cette n’approche n’exclue pas, par ailleurs, l’existence d’une (ou plusieurs) mémoire à plus long terme; ces aspects, cependant, se distinguent conceptuellement du cadre proprement local que nous envisageons pour étudier la protension et la rétention.
La forme de la rétention sera donc :
est le temps auquel se produit un événement faisant l’objet de la rétention, est l’instant de la description ( ); est le temps caractéristique associé à la décroissance de la rétention au fur et à mesure que l’on s’éloigne de la survenue de l’événement et est un coefficient décrivant le poids initial de la rétention et qui peut être associé à un individu ou à une espèce, par exemple, et permet notamment la comparaison avec d’autres organismes dont les facultés en la matière pourraient être plus ou moins développées.
Si l’analogie avec la physique a permis de poser assez naturellement une expression pour la rétention, il en va différemment pour la protension qui n’a pas d’analogue dans l’étude de l’inerte. Nous proposons donc de la rendre mathématiquement intelligible par symétrie temporelle par rapport à (le temps changeant de signe). Par une symétrie de la forme des fonctions impliquées, brisée par une valeur différente des paramètres pertinent ( et ), nous définissons donc la protension virtuelle. le qualificatif de virtuel sert à mettre en évidence le fait qu’elle fera intervenir le temps , qui concerne l’événement à anticiper et qui se trouve dans le futur de l’instant présent ( ). Nous obtenons donc :
où les différents paramètres, et , jouent le même rôle mutatis mutandis que ceux qui interviennent dans , voir figure 6. Remarquons ici que la protension virtuelle est une fonction croissante du temps, atteignant un maximum lorsque l’événement virtuel doit arriver.
Enfin, nous définirons la protension effective comme produit de la rétention et de la protension virtuelle :
On remarquera que, comme stipulé ci-dessus, une telle protension ne peut exister, que si elle est accompagnée (et même plutôt précédée), sous une forme ou sous une autre, par une sorte de “mémoire” (la rétention) relative à l’événement qu’il s’agit d’anticiper. Il s’agit ici d’une hypothèse forte, qui est néanmoins plausible, et qui maintient une forme de causalité malgré la participation dans la détermination à un instant d’un futur virtuel à un instant . Ainsi nous obtenons deux termes formellement symétriques, rétention et protension virtuelle, dont la combinaison produit la protension, terme décrivant l’action effective de l’organisation biologique sur elle-même dans le cadre de cette constitution locale du présent étendu.
Dans le cas où (absence complète de rétention) la protension s’annule du fait qu’il n’existe plus de référent qui permette d’anticiper un tant soit peu l’événement pertinent[3].
Toujours d’un point de vue phénoménologique, on s’attendra, en général à ce que , c’est-a-dire que le temps caractéristique de la rétention soit plus grand que celui associé à la protension virtuelle (pour “prévoir” il faut d’abord et encore plus se “souvenir”). Il ne s’agit cependant pas ici d’un point principiel comme l’hypothèse précédente. La contribution de dans la définition de (la deuxième exponentielle en ), évolue alors bien plus rapidement que celle de la rétention pour une même durée concernée. Par ailleurs, on aura toujours , comme fonctions du temps , et ceci pour n’importe quelle valeur de et ( n’étant réalisée qu’au moment même où le temps à anticiper est le présent exact, c’est-a-dire pour et donc ).
3.4 Analyse
3.4.1 Inertie biologique
Pour mieux rendre explicite le rôle du paramètre , par rapport à l’intervalle et aux temps caractéristiques et , quelques manipulations algébriques permettent de mettre l’expression de sous la forme du produit d’une fonction de et de deux coefficients dépendant uniquement de et , soit :

Pour comprendre cette décomposition, considérons dans un premier temps un phénomène de relaxation en physique, typiquement ayant la forme . Pour , nous pouvons écrire comme
Le coefficient indépendant de , , est le “résidu’ ’ au temps et peut être compris comme une forme “d’inertie” de la quantité concernée par la relaxation (par exemple cette quantité correspond à ce qu’il reste au temps d’un composé qui disparaît avec un temps caractéristique ). Ce coefficient ne dépend pas de mais décroit en fonction de .
Dans l’équation (11) nous avons deux facteurs indépendant de :
La première exponentielle correspond donc, par analogie à une inertie de type physique (dans un phénomène de relaxation), nous la noterons donc . Nous considérerons alors que le second terme représente une forme d’inertie proprement biologique (dépendant notamment des propriétés en matière de protension de l’organisme considéré, via ). Nous poserons donc :
La protension peut alors être considérée comme fonction du temps (modulée par des constantes et des temps caractéristiques), d’une inertie de type physique (correspondent à la baisse de la protension en ) et d’une inertie proprement biologique. Cette dernière est à comprendre comme un “traînage par continuité” de la stabilité (structurelle) présente; sorte de pari du vivant d’une permanence de sa propre structure et de celle du monde sensible, corrélé à la rétention (voir aussi les sections suivantes).
3.4.2 Protension globale
Pour évaluer l’effet de la protension sur un organisme, pour un couple d’événements donnés, nous pouvons considérer la quantité totale de protension que l’activité biologique met en jeu pour ces événements en faisant l’intégrale de la protension sur l’intervalle considéré :
On remarquera que cette quantité dépend uniquement de la longueur de l’intervalle . De plus, elle dépend de termes antagoniques, ce qui correspond à l’analyse qualitative suivante. Si l’intervalle de temps considéré est trop court, la protension n’a pas le temps d’agir sur l’organisation biologique, et son effet tend à s’annuler lorsque la longueur de l’intervalle tend vers . Au contraire, si l’intervalle de temps est trop grand, la protension virtuelle n’est pas appuyée par une rétention suffisamment forte pour être active (du côté de et conformément à nos hypothèses) et, réciproquement, du côté de , la rétention n’est pas associée à une protension virtuelle suffisamment forte pour avoir des effets importants. Ce dernier point est intéressant à mentionner car il redonne une certaine symétrie aux termes protensifs et rétensifs en cela que l’effectivité de la rétention passe par la protension.

Ces termes antagoniques conduisent dès lors à l’existence d’une longueur , optimale pour les effets de protensions et de rétention, et qui caractérise la taille de l’extension temporelle de l’organisme considéré.
3.5 Discussion
D’un point de vue cognitif, les situations où la notion de protension semble valide, voire nécessaire, pour comprendre les phénomènes semblent nombreuses. Citons tout d’abord le système nerveux des mammifères dont aucune des parties ne se contente de“transmettre” de l’information et de réagir, mais au contraire élabore, prolonge et anticipe, voir par exemple Berthoz 1997. Mais d’autres exemples peuvent être trouvés chez les unicellulaires. Ainsi, une paramécie entourée de sel, substance létale pour elle, fera quelques tentative pour trouver un passage, puis tentera un passage en force Misslin 2003. Ce type de comportements nous semble manifeste d’une organisation temporelle déjà avancée, puisqu’elle suppose une certaine forme “d’impatience”, basée sur la rétention des tentatives précédentes. Un autre exemple intéressant se trouve chez l’amibe, voir Saigusa et al. 2008. Une amibe soumise à trois agressions régulièrement espacées dans le temps est capable d’anticiper une quatrième agression possible (elle “réagit” quand le quatrième stimulus devrait avoir lieu, alors même qu’elle n’est pas perturbée), voire anticipe, sans stimulus supplémentaires jusqu’à trois agressions supplémentaires. Le dispositif employé est assez simple : l’amibe se déplace à une vitesse régulière, lors des trois stimuli (espacés régulièrement de ), elle ralentit de manière importante, puis sans stimulus supplémentaire la plupart des amibes ralentissent aussi après le dernier stimulus et , et certaine ralentissent encore après voire . On peut noter de plus que dans ce contexte, il y a une valeur pour laquelle l’effet de la protension est la plus importante (sans que cette optimalité se présente de manière aiguë).
Nous avons de plus obtenu une formulation pour l’inertie biologique. Remarquons qu’un tel concept a déjà été proposé pour décrire le comportement du système immunitaire Vaz et Varela 1978, dans le contexte théorique plus large de l’autopoïese — où le point de vue théorique se centre sur l’organisation biologique en tant qu’ensemble de processus se maintenant et maintenant ses conditions d’existence. Ce type d’idée est aussi présent autour des questions concernant la dynamique à grande échelle en neurologie, via la notion de “centre dynamique” (dynamic core) dans Edelman et Tononi 2000; Le Van Quyen 2003. Dans ce contexte aussi, donc, l’interprétation de la situation en terme “d’inertie active” semble utile, l’inertie biologique apparaissant alors comme la conséquence de l’activité interne, autonome, de l’organisme. L’autonomie de ce temps biologique est alors constituée à la fois d’une certaine indépendance vis à vis de l’environnement, engendrée par la dynamique de l’organisme, et d’une plus grande “adhésion” ou adéquation aux phénomènes, permise par la protension (voir la section 3.1). Cette combinaison peut aussi être interprétée comme une sortie du cadre de la théorie de l’information (dans laquelle les signaux sont traités pour faire ressortir les éléments pertinents) au profit “d’hypothèses” faites par l’organisme sur lui-même et sur environnement, faisant alors apparaître la pertinence du concept associé d’erreur[4]. De manière générale, il convient de noter que l’inertie biologique est à la fois basée sur une certaine stabilité des événements auxquels elle s’applique et surtout sur la stabilité structurelle, dynamique, de l’organisme.
Notons de plus que la structure de la protension permet d’identifier des degrés différents de complexité de la structure temporelle des organismes considérés. Ainsi, nous considérerons qu’à inertie biologique égale (ou avec un point de vue légèrement différent, à protension globale égale), un organisme pour lequel sera plus grand aura une complexité plus grande car il pourra avoir une activité protensive vis à vis d’événements plus distants. On remarquera qu’alors la protension effective sera plus localisée à proximité de .
4 Conclusion
Nous avons montré quelques aspects de l’organisation temporelle en biologie. Tout d’abord les rythmes biologiques peuvent être classés en deux catégories, en fonction de leurs invariants : les rythmes externes dont les propriétés les plus basique ne dépendent pas de l’organisme considéré et les rythmes internes, dépendant notamment de la masse adulte et du développement de l’organisme considéré. Cette distinction nous a amené à proposer une structure temporelle adéquate, marquée par une temporalité double. Nous avons ainsi ajouté au temps linéaire de la physique une seconde dimension, compacifiée (c’est à dire ayant la topologie d’un cercle), et formulée de manière à tenir compte de cette forme originale d’invariants temporels qu’engendrent les rythmes internes. Ce premier point peut déjà être considéré par lui-même comme une forme de phrasé biologique du temps physique en tant qu’organisation temporelle supplémentaire, ajoutée à la structure et aux symétries du temps physique usuel.
On peut cependant aller plus loin dans l’analyse car l’invariance associée au temps biologique concerne plutôt des nombres purs, “détachés” dès lors, de la dimensionalité du temps physique. Nous pouvons même aller plus loin dans l’analyse en termes de phrasé. En effet, ce qui fonde en général la rythmicité des phénomènes physiques est généralement la conservation d’un niveau d’énergie, définissant les propriétés du phénomène (plus généralement encore, l’on peut dire que ce sont les symétries en jeu dans le cadre théorique que l’on utilise et qui conduisent à une trajectoire temporelle spécifique, voir Bailly et Longo 2011, 2008a; Longo et Montévil 2011). Or, le cadre théorique que nous proposons pour l’étude du vivant, la criticité étendue, est au contraire basée sur la brisure de ces symétries, ainsi il devient, à notre sens, impossible de fonder une correspondance “précise” (au sens d’une trajectoire spécifique) entre ce temps biologique et temps physique. Cet aspect peut être abordé de manière tout à fait élémentaire si l’on considère par exemple le rythme cardiaque : non seulement l’analyse de l’organe qu’est le cœur ne passe pas par un oscillateur physiquement élémentaire fondant le rapport entre cycle cardiaque et temps physique Noble 2006 (autrement dit il n’y a pas d’horloge interne séparée déterminant la rythmicité du rythme cardiaque), mais le régime causal de la rythmicité cardiaque n’est pas basé (uniquement) sur un système possédant une forme physiquement usuelle d’invariance dans l’organisation dynamique du cœur, y compris émergente. Au contraire, ce régime causal implique directement l’organisme dans sa globalité, en tant qu’il a une histoire (tant aux temps courts que longs), un contexte, …Partant, la réduction du temps biologique au temps physique — que l’on pourrait voir comme une projection — nous semble impossible (non-objective) dans le contexte de l’organisme, y compris localement, car non-fondée sur une invariance (sauf certains comportements moyens).
Le second aspect du temps biologique que nous avons considéré ici est la constitution par le vivant d’une structure temporelle locale, que nous avons décrit en terme de rétention et de protension. Cette approche conduit alors à une forme de présent étendu possédant une structure interne, la temporalité biologique y étant abordée comme constituée d’une tension entre un passé proche et un futur virtuel. Nous pouvons, dans ce cas aussi, parler de “phrasé” au sens où l’organisme constitue une temporalité en décalage (ce qui implique aussi une correspondance, au moins partielle) avec la temporalité proprement physique. Cette forme de phrasé a alors ceci d’original qu’elle passe par une forme d’inertie et que cette inertie engendre dans certains cas l’erreur. Notons que cet aspect est principiel car la protension passe la protension virtuelle que nous avons formalisé comme “rétention” d’un événement n’ayant pas encore eu lieu et qui donc n’aura pas obligatoirement lieu, la condition d’établissement d’une telle causalité d’un futur virtuel sur le présent étant la présence d’une rétention d’un événement passé.
Les aspects dont nous avons développé une théorisation dans ce texte, n’épuisent pas, bien entendu, la richesse des formes de temporalité constituées par les phénomènes biologiques. Dans le prolongement des aspects que nous avons décrit, nous pouvons par exemple pointer la question des rapports entre rythmes internes, par delà les correspondances de leurs périodes moyennes du point de vue de l’allométrie. Pour des rythmes internes proches du point de vue de leurs périodicités, tels que les cycles cardiaques et respiratoires, différentes formes de variabilités corrélées sont rencontrées, ce qui semble indiquer que leurs liens sont complexes Schäfer et al. 1999; Song et Lehrer 2003. Suivant un point de vue différent, le rapport entre protension/rétention et les rythmes biologiques se joue à l’intérieur de l’organisme, l’itération des rythmes internes engendrant un “substrat temporel” sur lequel l’activité protensive, cellulaire par exemple, peut s’appuyer de manière privilégiée.
Note : Des versions préliminaires ou revues des articles de Longo et Montévil sont téléchargeables sur http://www.di.ens.fr/users/longo et http://www.montevil.org respectivement.
Références
- Bailly, F. 1991. « L’anneau des disciplines ». Revue Internationale de Systémique 5 (3).
- Bailly, F., F. Gaill et R. Mosseri. 1993. « Orgons and biolons in theoretical biology : Phenomenological analysis and quantum analogies. » Acta Biotheoretica 41 (1–2) : 3-11. doi : 10.1007/BF00712769. (Cf. page 19).
- Bailly, F., et G. Longo. 2008a. « Extended critical situations : the physical singularity of life phenomena ». Journal of Biological Systems 16 (2) : 309. doi : 10.1142/S0218339008002514. (Cf. pages 5, 31, 44).
- _________. 2008b. « Schèmes géométriques pour le temps biologique ». In Sciences du vivant et phénom énologie de la vie, sous la direction de P.A. Miquel. Noesis-Vrin. (Cf. pages 1, 50).
- _________. 2011. Mathematics and the natural sciences; The Physical Singularity of Life. London : Imperial College Press. (Cf. pages 5, 31, 44).
- Bailly, F., G. Longo et M. Montévil. 2011. « A 2-dimensional geometry for biological time ». Progress in Biophysics and Molecular Biology 106 (3) : 474-484. issn : 0079-6107. doi : 10.1016/j.pbiomolbio.2011.02.001. (Cf. pages 1, 4 sq., 19 sq., 50).
- Berthoz, A. 1997. Le sens du mouvement. Odile Jacob. (Cf. pages 31, 43).
- Botzung, A., E. Denkova et L. Manning. 2008. « Experiencing past and future personal events : Functional neuroimaging evidence on the neural bases of mental time travel ». Brain and Cognition 66 (2) : 202-212. doi :10.1016/j.bandc.2007.07.011. (Cf. page 50).
- Bourgine, P., et J. Stewart. 2004. « Autopoiesis and cognition ». Artificial Life 10 : 327. doi :10.1162/1064546041255557.
- Chaline, J. 1999. Les horloges du vivant : un nouveau stade de la théorie de l’ évolution? Hachette Littératures.
- Edelman, G.M., et G. Tononi. 2000. « Reentry and the dynamic core : neural correlates of conscious experience ». In Neural Correlates of Consciousness : Empirical and Conceptual Questions, sous la direction de T. Metzinger, 139-151. MIT Press. (Cf. pages 30, 44).
- _________. 2001. A universe of consciousness : How matter becomes imagination. Basic Books. (Cf. page 30).
- Feynman, R.P., H. Isaac, J.M. Lévy-Leblond et F. Balibar. 1980. La nature de la physique. Seuil. (Cf. page 4).
- Gang, Y., et M. Malik. 2003. « Heart rate variability analysis in general medicine ». Indian Pacing and Electrophysiology Journal 3 (1) : 34. (Cf. page 29).
- Goldberger, A.L., L.A.N. Amaral, L. Glass, J.M. Hausdorff, P.C. Ivanov, R.G. Mark, J.E. Mietus, G.B. Moody, C.-K. Peng et H.E. Stanley. 2000. « PhysioBank, PhysioToolkit, and PhysioNet : Components of a New Research Resource for Complex Physiologic Signals ». Circulation 101, no 23 (juin) : e215-e220. doi : 10.1161/01.CIR.101.23.e215. (Cf. pages 25, 28).
- Horsfield, K. 1977. « Morphology of branching trees related to entropy. » Respiration Physiology 29 (2) : 179. doi : 10.1016/0034-5687(77)90090-1.
- Le Van Quyen, M. 2003. « Disentangling the dynamic core : a research program for a neurodynamics at the large-scale ». Biological Research 36 : 67-88. doi : 10.4067/S0716-97602003000100006. (Cf. page 44).
- Lecointre, G., H. Le Guyader et D. Visset. 2001. Classification phylogéné tique du vivant. Belin.
- Lindstedt, S.L., et W.A. Calder III. 1981. « Body size, physiological time, and longevity of homeothermic animals ». Quarterly Review of Biology : 1-16. doi : 10.1086/412080. (Cf. pages 8 sq.).
- Longo, G., et M. Montévil. 2011. « Protention and retention in biological systems ». Theory in Biosciences 130 (2) : 107-117. issn : 1431-7613. doi : 10.1007/s12064-010-0116-6. (Cf. pages 1, 4 sq., 19, 30 sq., 44, 50).
- Malik, M., J.T. Bigger, A.J. Camm, R.E. Kleiger, A. Malliani, A.J. Moss et P.J. Schwartz. 1996. « Heart rate variability : Standards of measurement, physiological interpretation, and clinical use ». European Heart Journal 17 (3) : 354. doi :10.1161/01.CIR.0000140765.71014.1C. (Cf. page 29).
- Massin, M.M., K. Maeyns, N. Withofs, F. Ravet et P. Gerard. 2000. « Circadian rhythm of heart rate and heart rate variability. » Archives of Disease in Childhood 83 (2) : 179-182. doi : 10.1136/adc.83.2.179. (Cf. page 29).
- McMahon, T.A. 1980. « Scaling physiological time ». In Some mathematical questions in biology, 13 : 131. Amer Mathematical Society. isbn : 0821811630. (Cf. page 4).
- Misslin, R. 2003. « Une vie de cellule ». Revue de Synthèse 124 (1) : 205-221. doi : 10.1007/BF02963405. (Cf. page 43).
- Montévil, M. 2012. « Géométrie du temps biologique : rythmes et protension ». In Questions de phrasé, sous la direction d’A. bonnet, F. Nicolas et T. Paul. Article invité. Hermann, janvier. isbn : 978-2705681555. (Cf. pages 1, 50).
- Noble, D. 2006. The music of life. Oxford : Oxford U. P. (Cf. page 45).
- Overduin, J.M., et P.S. Wesson. 1997. « Kaluza-Klein Gravity ». Physics Reports 283 : 303-380. doi :10.1016/S0370-1573(96)00046-4. (Cf. page 50).
- Peters, R.H. 1986. The ecological implications of body size. Cambridge U. P.
- Rosen, R. 1991. Life itself : a comprehensive inquiry into the nature, origin, and fabrication of life. Columbia U. P.
- Saigusa, T., A. Tero, T. Nakagaki et Y. Kuramoto. 2008. « Amoebae anticipate periodic events. » Physical Review Letters 100 (1) : 018101. doi : 10.1103/PhysRevLett.100.018101. (Cf. page 43).
- Savage, V.M., J.F. Gilloly, W.H. Woodruff, G.B. West, A.P. Allen, B.J. Enquist et J.H. Brown. 2004. « The predominance of quarter-power scaling in biology ». Ecology 18 : 257-282. doi : 10.1111/j.0269-8463.2004.00856.x. (Cf. page 9).
- Schäfer, C., M.G. Rosenblum, H.H. Abel et J. Kurths. 1999. « Synchronization in the human cardiorespiratory system ». Physical Review E 60 (1) : 857-870. doi : 10.1103/PhysRevE.60.857. (Cf. page 45).
- Schmidt-Nielsen, K. 1984. Scaling. Cambridge U. P. (Cf. page 9).
- Song, H.S., et P.M. Lehrer. 2003. « The effects of specific respiratory rates on heart rate and heart rate variability ». Applied psychophysiology and biofeedback 28 (1) : 13-23. doi : 10.1023/A:1022312815649. (Cf. page 45).
- Suzuki, M., K. Kaneko et S. Takesue. 1982. « Critical Slowing Down in Stochastic Processes. I ». Progress of Theoretical Physics 67 (6) : 1756-1775. doi : 10.1143/PTP.67.1756. (Cf. page 31).
- Szpunar, K.K., J.M. Watson et K.B. McDermott. 2007. « Neural substrates of envisioning the future ». Proceedings of the National Academy of Sciences 104 (2) : 642. doi : 10.1073/pnas.0610082104. (Cf. page 50).
- Van Gelder, T. 1999. « Wooden iron? Husserlian phenomenology meets cognitive science ». In Naturalizing Phenomenology : Issues in Contemporary Phenomenology and Cognitive Science, sous la direction de J. Petitot, F.J. Varela, B. Pachoud et J.M. Roy, 245-265. Stanford U. P. (Cf. page 30).
- Varela, F.J. 1989. Autonomie et connaissance. Paris : Seuil.
- _________. 1997. « Patterns of life : Intertwining identity and cognition ». Brain and Cognition 34 (1) : 72-87. doi : 10.1006/brcg.1997.0907.
- _________. 1999. « The specious present : A neurophenomenology of time consciousness ». In Naturalizing phenomenology : Issues in contemporary phenomenology and cognitive science, sous la direction de J. Petitot, F.J. Varela, B. Pachoud et J.M. Roy, 266-314. Stanford U. P. (Cf. page 30).
- Vaz, N.M., et F.J. Varela. 1978. « Self and non-sense : an organism-centered approach to immunology. » Medical Hypotheses 4 (3) : 231-267. doi : 10.1016/0306-9877(78)90005-1. (Cf. page 43).
- Waddington, G.H. 1977. « Stabilisation In Systems : Chreods and epigenetic landscapes ». Futures 9 (2) : 139-146. issn : 0016-3287. doi : 10.1016/0016-3287(77)90006-4.
- West, G.B., et J.H. Brown. 2005. « The origin of allometric scaling laws in biology from genomes to ecosystems : Towards a quantitative unifying theory of biological structure and organization. » Journal of Experimental Biology 208 (9) : 1575-1592. doi :10.1242/jeb.01589. (Cf. page 4).
- Winfree, A.T. 2001. The geometry of biological time. Second. Springer Verlag. (Cf. page 4).


