Changements de symétrie, criticité et aléatoire : Mathématiques et objectivation du vivant

Changements de symétrie, criticité et aléatoire : Mathématiques et objectivation du vivant

Symmetry changes, criticality and randomness: Mathematics and objectivation in biology

Maël Montévil

Postdoctorat CNRS, IHPST (UMR 8590), financement Île-de-France, DIM ISC.

Abstract

Ce texte présente un modèle pour le temps biologique ainsi qu’un certain nombre d’idées plus générales sur l’articulation entre mathématiques et objets biologiques, fondées sur des propositions théoriques. Nous décrivons d’abord un modèle géométrisant le temps des mammifères, basé en partie sur la notion d’allométrie. Ce modèle permet de mettre en évidence la structure de la variabilité des rythmes biologiques et de discriminer cas sains et cas pathologiques. Nous utilisons cet exemple pour illustrer les principes permettant la mathématisation.

Nous discutons comment s’articulent mathématiques et définition théorique des objets physiques. Nous mettons en particulier l’accent sur le rôle que jouent les symétries théoriques pour justifier ces définitions, tant au niveau de la constitution d’un espace de description que de l’obtention d’équations déterminant la trajectoire suivie par un objet. Nous abordons aussi les transitions de phases comme situations paradigmatiques où les symétries d’un système changent.

Ceci nous amène à proposer que les objets biologiques (organismes, cellules) sont caractérisés par une instabilité de leurs symétries théoriques. Les objets prennent alors un sens différent de celui qu’ils ont en physique : ils font preuve de variabilité et sont fondamentalement historiques. Ceci n’empêche pas la présence d’éléments de stabilité chez le vivant, mais  les symétries biologiques  prennent un sens différent des symétries fondamentales de la physique.

Mots clés : allométrie, variabilité, rythmes cardiaques, historicité biologique, mesure

Abstract

This text presents a model for biological time and more general ideas on the articulation between mathematics and biological phenomena, in association with theoretical proposals. We describe first a geometrization of the temporal organization of mammals, on the basis, in particular, of the notion of allometry. This model allows exploring the variability of biological rhythms and discriminating between healthy and several pathological cases. We also use this example to discuss the principles which are used for the mathematization.

Then, we discuss the articulation between mathematics and the theoretical definition of physical objects. We emphasize the role of symmetries in order to justify these definitions, both at the level of the description space and at the level of the equations which entail the trajectory of a system. We also discuss the case of phase transitions where a symmetry change corresponds to a change of behavior of the system.

This leads us to propose that biological objects (cells, organisms,...) have unstable theoretical symmetries. Then the objects have different features : they exhibit variability and are fundamentally historical. It does not imply that there would not exist elements of stability in biological systems, but they have a different meaning than in physics.

Keywords : allometry, variability, cardiac rhythms, biological historicity, measurement

1 Introduction

Pour commencer ce texte, il convient de préciser le type de questionnement sur lequel porte notre discussion. Nous aborderons la question du cadre théorique qu’il nous semble pertinent de développer en biologie. Ici nous entendons théorie en un sens qui a une certaine spécificité, en effet, théorie et modélisation sont parfois confondus, en particulier en biologie. Proposer un cadre théorique est un acte particulier, il revient à proposer une nouvelle manière de voir et de constituer les phénomènes comme objets de connaissance. En tant que telle, toute proposition théorique porte un caractère d’étrangeté car elle implique un nouveau regard. Ainsi, le monde proposé par la mécanique quantique se distingue radicalement du monde de la mécanique classique... mais le caractère parfois considéré comme naturel de cette dernière vient surtout de son enracinement dans notre culture et procède donc à notre avis surtout d’une certaine accoutumance.

Nous ne pouvons nous dispenser d’expliciter un point épistémologique avant de poursuivre. Celui-ci concerne le sens donné aux théories. Ce sens a évolué au cours de l’histoire, mais des connotations anciennes persistent parfois, implicitement, dans des méthodologies actuelles. Pour Galilée, par exemple, la théorie donne un accès immédiat à la réalité, ceci est explicitement justifié par un contexte théologique : pour lui, Dieu a écrit le monde en langage mathématique et il ne reste aux hommes qu’à découvrir ce « texte ». Ce sens donné aux  théories est bien évidemment daté et l’évocation du divin comme garant de nos connaissances, comme chez Descartes, n’est plus acceptable. Nous pouvons l’opposer à la notion de théorie comme cadre conceptuel, parfois mathématisé, permettant d’objectiver des phénomènes, c’est-à-dire de les rendre intelligibles tout en réduisant les aspects arbitraires utilisés pour leur appréhension. Cette différence a des implications concrètes pour la méthodologie scientifique.

La première de ces implications concerne la notion d’incomplétude : les théories peuvent permettre de prouver qu’elles ne peuvent pas appréhender certains phénomènes, ou qu’elles peuvent le faire mais avec des  limitations particulières. Ainsi, les situations chaotiques sont des situations où le cadre classique permet de montrer son incapacité à prédire des trajectoires (bien qu’elles soient déterminées par cette théorie)^[1].

La seconde est le rôle fondamental donné à la notion de mesure, comme description théorique de ce que signifie l’accès à l’objet dans l’expérience. La mesure en mécanique quantique est un exemple particulièrement clair de cette situation car dans ce cas l’état est transformé par la mesure. Nous esquisserons une notion de mesure adaptée à la biologie à la fin de ce texte.

Enfin la dernière de ces implications est que, face à des phénomènes radicalement différents de ceux que les théories existantes permettent d’aborder, il est souvent nécessaire de proposer une théorie originale, ce qui n’exclue pas des projets d’unification ultérieure.  Ce point est particulièrement en phase avec l’histoire de la physique : cette discipline a en effet proposé la mécanique classique pour le mouvement des corps, puis la thermodynamique pour comprendre la chaleur et plus généralement les systèmes constitués d’un grand nombre d’objets similaires, puis la physique quantique pour les objets microscopiques et la relativité générale pour la gravitation, mais aussi la mécanique des fluides, la théorie des phénomènes critiques, …

Dans ce contexte, il est donc naturel de proposer, répétons-le, dans la lignée de ce qui a été fait en physique, que les situations biologiques nécessitent une théorie originale. Dans ce texte, nous proposerons une manière d’aborder théoriquement plusieurs aspects des situations biologiques dont les théories physiques existantes ne savent pas rendre compte. En particulier, le vivant a un caractère historique, et toutes les expériences faites en biologie sont faites sur des organismes issus d ’environ 3,8 milliards d’année d’évolution. Cette historicité est couplée à une variabilité fondamentale : le vivant change son organisation avec le passage du temps. Enfin, les organismes possèdent une structure de cohérence particulière, de telle sorte que leurs parties sont interdépendantes. De plus, nous aborderons la question du sens que peut prendre la mesure en biologie, cette question n’ayant pour ainsi dire pas été abordée dans la littérature. Pour introduire ces questions, nous allons dans un premier temps aborder la question spécifique de certains aspects du temps biologique, qui nous permettra de poser et d’illustrer certains problèmes de la mathématisation en biologie.

2 Géométrie du temps des mammifères

2.1 Introduction

Dans cette section, nous allons introduire un cadre géométrique pour aborder certains aspects de la temporalité des mammifères, ces idées ont été proposées ici^[2]. Nous insisterons en particulier sur la méthodologie et les hypothèses utilisées, de sorte que cette partie a aussi un rôle introductif pour le reste de ce texte. Chaque théorie physique spécifie la nature, théorique et mathématique, de son appréhension du temps. Ainsi, le temps est inséparable de l’espace dans la relativité générale, alors que dans la mécanique quantique il a le rôle d’un paramètre, rôle tout à fait hétérogène de celui des positions et vitesses qui sont des observables (mesurables, et donc appréhendées mathématiquement par un opérateur). Plus proche, en termes d’échelles, de la biologie, le temps de la mécanique classique est un paramètre, et comporte une symétrie par renversement du temps : si l’on regarde un film de ces phénomènes, il n’est pas possible de savoir s’il est diffusé normalement ou à l’envers. Ceci correspond à une symétrie des équations fondamentales de la mécanique classique par le remplacement de t par -t. La thermodynamique, elle, brise cette symétrie par l’introduction d’une grandeur non-conservative, l’entropie, qui ne peut que croître dans un système isolé. Qu’en est-il donc pour le temps des organismes, et pour le cas qui nous occupe plus spécifiquement, le cas des mammifères ? Pour définir un temps approprié aux phénomènes qui nous intéressent, il convient, en suivant la méthodologie employée en physique, de se baser sur les régularités de ces phénomènes. Ainsi, Einstein lie le temps à l’espace parce que les transformations de l’espace (changements de systèmes de référence) impliquent des transformations du temps (à cause de l’invariance de la vitesse de la lumière, qui étant une vitesse, lie le temps et l’espace). De manière similaire, l’irréversibilité du temps en thermodynamique correspond à des transformations qui ne peuvent se produire que dans une direction pour les systèmes isolés, la dispersion d’un gaz dans une pièce par exemple.

En biologie, l’on peut distinguer (au moins) deux types de temporalités. La première correspond à une friction avec des phénomènes physiques dont les propriétés sont indépendantes des organismes considérés : ainsi le cycle jour-nuit contraint de l’extérieur l’organisation temporelle du vivant. La réponse biologique à ce type de contrainte est, par contre, variable, tant au niveau évolutif (animaux diurnes ou nocturnes, …) qu’au niveau de l’organisme particulier (avec l’exemple du décalage horaire). Le second aspect du temps biologique que nous allons discuter concerne une temporalité dépendant surtout du système concerné, ainsi l’on constate que l’espérance de vie d’une souris est d’environ deux ans, alors que celle d’un chien est d’environ dix ans, et que les fréquences cardiaques varient proportionnellement.

2.2 Allométries

Ce second aspect du temps biologique peut être décrit dans une large mesure par la notion d’allométrie. L’idée en est très simple, il s’agit de regarder comment une quantité varie en fonction de la taille du système considéré. Ainsi, lorsque l’on regarde un objet, tel qu’un cube, l’on constate que si l’on multiplie toutes les longueurs par un facteur l, alors toutes les aires seront multipliées par un facteur l² et tous les volumes par un facteur l3. Les exposants concernés, 2 et 3 ici, caractérisent de manière fondamentale les quantités correspondantes (surfaces et volumes respectivement). Ceci suppose bien évidemment que la forme considérée est maintenue de sorte que seule la taille de l’objet est changée. En termes techniques, l ’allométrie se base sur une symétrie entre objets de tailles différentes, et permet de montrer les propriétés de cette famille d’objets. Plus précisément, elle parle d’un objet générique, dont la taille est un paramètre, ainsi que des quantités utilisées pour le décrire. Ce type d’analyses a été appliqué en biologie dès la fin du XIX par Rübner^[3], le raisonnement était alors que le métabolisme devait être proportionnel aux surfaces extérieures, à cause des pertes de chaleur, donc R˜S˜l². La masse est proportionnelle à un volume, donc  M˜V˜l3, ce qui conduit finalement à R˜M2/3. Le point théorique et méthodologique qui est crucial ici est la mise en évidence d’une propriété biologique par la transformation (mathématique) de la masse. Plus précisément, l’idée est que divers organismes de tailles différentes (de masses différentes) vont avoir le même « fonctionnement », et dans l’hypothèse de Rübner, à peu près les mêmes formes, de sorte que le passage d’un organisme à l’autre se limiterait aux conséquences d’un changement du rapport entre surface et volume associé à la dilatation d’une forme géométrique euclidienne (une des astuces étant que la forme n’a pas besoin d’être précisée du moment que la transformation est la dilatation d’une forme euclidienne). L’hypothèse de Rübner a été ensuite invalidée par Kleiber, montrant plutôt la pertinence d’un exposant autour de 0.75 parmi les mammifères adultes, dans des conditions de métabolisme basal^{[4] [5]}. Notons juste ici que cette question est toujours l’enjeu de débats parfois vifs, tant sur la stabilité de cet exposant que sur son interprétation. Certains travaux proposent par exemple un raisonnement analogue à Rübner, mais basé sur une géométrie fractale proposée où la contrainte serait le transport de l’oxygène^[6]. Un métabolisme est typiquement une énergie divisée par un temps. En première approximation, on peut considérer que l’énergie est proportionnelle à la masse, ce qui implique que pour R˜Ma, on a un temps $\tau$0˜Mb˜M1-a, en particulier pour a=0.75, b=0.25. L’un des intérêts de déplacer le centre de gravité de ce type d’analyse vers la question du temps est qu’alors qu’il n’y a qu’un métabolisme pour un organisme, il y a de nombreux rythmes et temps caractéristiques pertinents pour ce même organisme, et ils sont mesurables expérimentalement (rythmes cardiaques, respiratoires, espérances de vie, clairance du sang, rythmes de contractions musculaires,...). Dans des conditions standards ces rythmes confirment empiriquement la pertinence de l’analyse en terme d’allométrie (et donc l’influence de la masse sur ces rythmes), ainsi qu’un exposant avoisinant 0.25 chez les mammifères (avec des résultats similaires pour les oiseaux)^[7].  Ces résultats empiriques permettent d’identifier un temps biologique, associés à ces dynamiques, où la masse intervient comme un paramètre dominant, et qui diffère donc radicalement des rythmes dont la période est déterminée par des invariants physiques, indépendants de l’organisme considéré.

2.3 Géométrie du temps biologique

Pour appréhender conjointement ces deux aspects de la temporalité biologique, nous avons proposé^[8] de partir du temps physique t et d’une dimension biologique supplémentaire $\theta$. Étant donné le caractère rythmique des phénomènes biologiques mentionnés, mais aussi parce que le temps biologique, qu’il soit évolutif ou ontogénétique est un temps qui a une origine et qui est marqué par des itérations, $\theta$ est une dimension compacifiée, et possède donc la topologie d’un cercle. Le temps pertinent est alors bidimensionnel, il forme une surface. Pour décrire cette surface, nous allons la plonger dans un espace tridimensionnel. La combinaison de t et de $\theta$ conduit alors à la description d’un tube. L’itération du temps biologique permet d’introduire la progression globale du temps biologique concerné, t’, comme axe orthogonal au temps physique t. Le tube correspondant au temps biologique est alors diagonal, dès lors que la progression du temps physique s’associe à une progression du temps biologique. L’on voit aussi comment un rythme physique tel que les rythmes circadiens va pouvoir intervenir dans l’organisation biologique du temps, en accélérant et  ralentissant alternativement sa progression. Plus précisément, on peut partir des itérations du temps biologique comme un terme Rexp(i(s(t)+ $\theta$)). La partie réelle de ce terme va correspondre à l’axe (t’) et la partie imaginaire au troisième axe (z). s(t) va alors être l’intégrale de la progression du temps biologique que l’on peut décomposer en deux termes : $\tau$((t-tb)/ $\tau$i) représente la progression moyenne du temps biologique vis-à-vis du temps physique, avec tb le temps de naissance de l’organisme considéré. Typiquement, $\tau$ ralenti progressivement lors du développement pour atteindre la vitesse $\tau$((t-tb)/ $\tau$i)=(t-tb)/( $\tau$0 M0.25)et’ chez l’adulte (parmi les mammifères). L’hypothèse sous-jacente est que, pour $\tau$, la même forme est pertinente pour des organismes ayant des masses adultes différentes. Il s’agit d’une hypothèse de symétrie entre ces organismes. Notons cependant que $\tau$ ou $\tau$i peuvent néanmoins être adpatés pour des phyla qui le nécessitent. À ceci s’ajoute g(t)=Re / $\omega$e $\tau$i exp(i( $\omega$e t + $\phi$))et’, qui représente l’impact d’un phénomène periodique physique considéré. Disons tout de suite que Re correspond au poids de ce phénomène sur l’activité biologique, le terme 1/ $\omega$e $\tau$i  correspond au nombre d’itérations du temps compacifié pendant une oscillation du rythme physique. L’hypothèse est alors que c’est Re qui est relativement invariant pour des organismes de différentes masses. $\phi$ correspond à la manière dont cet impact va se produire (par exemple les animaux diurnes et nocturnes sont en opposition de phase). L’avancée du temps biologique est alors donnée par la longueur de la courbe décrite par $\tau$((t-tb)/ $\tau$i)+g(t). La structure complète est donnée par f(t, $\theta$)= $\tau$((t-tb)/ $\tau$i)+g(t)+ Rexp(i(s(t)+ $\theta$)). Une discussion exhaustive des hypothèses de ce modèle et de leurs conséquences peut être trouvée ici^[9].

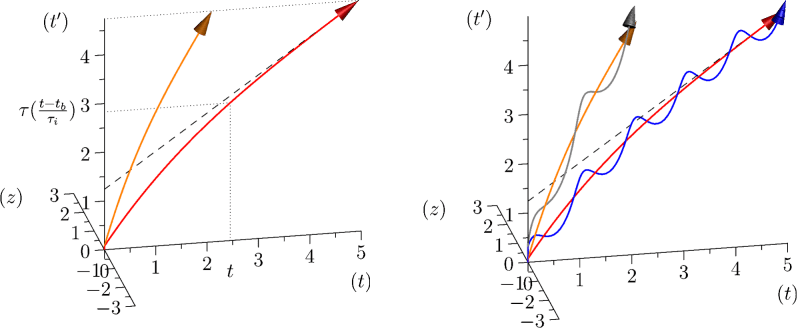
2.4 Structure de la variabilité du temps biologique

Pour l’instant nous avons surtout discuté notre cadre en lien avec l’allométrie interspécifique, et donc les vitesses moyennes du temps biologique. Notre cadre permet cependant aussi d’aborder les trajectoires individuelles de manière originale.

La structure temporelle des rythmes biologiques possède des propriétés singulières, caractérisée par des corrélations à longues distances et à toutes les échelles, ce qui est caractéristique de l’absence de pathologies^[10]. Cette situation remet notamment fortement en cause le concept d’homéostasie, c’est-à-dire l’articulation entre moyennes et normalité physiologique^[11].

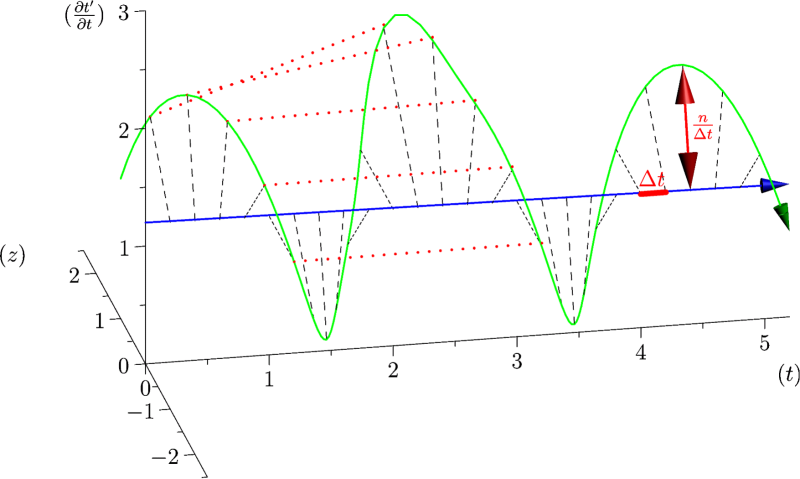
Pour étudier la variabilité des rythmes biologiques dans notre cadre, l’idée est d’utiliser une série temporelle empirique fournissant s(t). Il faut considérer $\partial$f / $\partial$t, en particulier le terme R exp(i(s(t)+ $\theta$)) devient iR ds(t)/dt exp(i(s(t)+ $\theta$)). Le point remarquable est que le rayon du temps compacifié devient proportionnel à ds(t)/dt=2 $\pi$/T(t), où T(t) est la durée d’une itération du temps compacifié, et donc dans le cas du rythme cardiaque le temps entre deux battements de cœur au moment t. Il est alors intéressant de changer l’échelle du temps compacifié. Si l’on considère n itérations de $\theta$ par itération de $\theta$n alors notre cadre permet de mettre en évidence la structure de la variabilité du rythme observé : si le rythme de $\theta$ est accéléré pendant n itérations, alors le rayon de la structure sera plus grand pendant une rotation de $\theta$n, et une accélération plus courte ne fera qu’une portion d’un tour.

Nous pouvons alors utiliser ce cadre avec des séries temporelles empiriques, par exemple de battements cardiaques. Il est connu que de telles séries sont complexes, non-stationnaires, et ont des dimensions fractales non-triviales mais qui ne semblent pas non plus constituer des invariants (elles ne sont pas stables)11.

La figure 3 montre le résultat de la procédure proposée dans le cas d’une patiente ne présentant pas de pathologie particulière. On remarque que la structure obtenue est d’une très grande richesse, possédant deux régimes distincts : pendant la nuit, le tube (et donc le rythme) est relativement régulier avec des accélérations limitées dans le temps, et ne faisant qu’une portion d’un tour dans la structure obtenue. Pendant le jour par contre, on remarque de nombreuses excroissances faisant un tour complet (ce qui n’exclue pas que l’accélération correspondante soit plus longue) et qui sont disposées de manière irrégulière.

Le caractère multi-échelle de la variabilité du rythme diurne est confirmé par la figure 4, où le nombre de battements par tour est doublé. La variabilité nocturne est réduite, alors que la partie diurne garde la même structure.

Enfin, ce mode de représentation permet d’aborder et de discuter des situations pathologiques. Les pathologies altèrent profondément la structure de la variabilité cardiaque, y compris dans les cas où la forme des battements apparaît comme normale (dans un électrocardiogramme).

2.5 Bilan

La géométrie que nous proposons pour le temps des mammifères est fondée sur deux ingrédients fondamentaux. Le premier est la présence de certaines régularités. L’invariance des périodicités physiques, bien évidemment, mais aussi des régularités biologiques moyennes telle que l’allométrie et le ralentissement des processus biologiques lors du développement. Une fois ce cadre posé, l’introduction d’une dimension supplémentaire pour le temps biologique, ainsi que les choix de notre formalisme permettent de s’adapter à des groupes biologiques ayant des caractéristiques différentes. Par exemple, $\tau$i pourra être changé pour les exceptions à l’allométrie ou la fonction $\tau$((t-tb)/ $\tau$i) pourra s’adapter à des développements différents (notons au passage que la forme de $\tau$ reste largement heuristique, elle ne dépend pas seulement de la courbe de croissance des organismes car l’allométrie entre jeunes et adultes n’est pas forcément la même, et tend à être plus variable, que l’allométrie entre adultes de différentes espèces). Le deuxième ingrédient, qui est déjà implicite dans la discussion ci-dessus, est l’autonomie de ces rythmes, associée à la variabilité biologique. Cette variabilité existe vis-à-vis de l’allométrie, mais nous l’avons surtout abordée dans le cas des trajectoires individuelles, où elle devient particulièrement forte et est l’enjeu principal de la seconde partie de notre discussion.

3 Phénomènes et mathématiques en physique

Dans cette partie, nous allons discuter de manière aussi simple et concise que possible la manière dont sont constitués théoriquement les objets physiques, en insistant sur le rôle des mathématiques et les implications de leur usage.

3.1 Symétries

Dans cette section et la suivante, la notion de symétrie sera centrale, et nous allons donc tout d’abord expliciter le sens que nous lui donnons ici. Notons que les idées développées le sont avec plus de détails dans^[12], voir aussi^[13]. Par symétrie nous entendons une transformation qui laisse invariants les aspects pertinents de l’objet considéré. Il est important de noter que nous ne nous restreignons pas aux symétries géométriques usuellement discutées en biologie telle que la symétrie bilatérale de certains organismes. Pour illustrer ce point et amorcer l’articulation avec les sciences de la nature, nous pouvons prendre l’exemple du comptage. Ainsi, il est possible de dire que cette page et la suivante forment deux pages au sens où elles peuvent être tournées, ont un format, une matière, etc qui sont équivalentes. Si l’on considère par contre le contenu, dans la mesure où l’auteur ne se répète pas outrageusement, ces deux pages ne sont plus équivalentes et forment un seul discours, de sorte que, par exemple, la lecture n’est plus possible si les pages sont permutées. Nous voyons donc par cet exemple très simple, que l’opération mathématique la plus élémentaire, 1+1=2 suppose une équivalence entre les objets qui sont considérés, et que cette équivalence dépend de ce qui est proposé comme pertinent dans l’appréhension de l’objet.  Notons aussi que la notion de symétrie est fondamentale pour les mathématiques^[14]. Pour exemplifier ceci, remarquons simplement que les mathématiques (y compris dans le contexte de la physique) arrivent à traiter aisément un nombre infini d’objets, alors que toute démonstration (ou tout calcul) reste fini. Cette capacité se comprend si l’on considère que cette infinité de termes peut être abordée de manière générique. Ainsi, l’on considère par exemple x plutôt que 1,95, mais il est alors nécessaire de pouvoir établir le raisonnement mathématique pour un x générique, indépendamment de sa valeur spécifique, et donc qu’une symétrie existe entre les différents x considérés (ceci se fait bien évidemment de manière extraordinairement riche et diverse suivant les cadres considérés).

3.2 Constitution théorique des objets physiques

Une particularité de la physique est que son appréhension de la nature est indissociable de l’usage des mathématiques. De manière schématique, l’on peut dire qu’une théorie physique fournit à la fois une définition des quantités pertinentes ainsi qu’une détermination théorique, prenant généralement la forme d’équations que les objets vérifient et permettant de comprendre la trajectoire des objets dans cet espace mathématique. Dans ce paragraphe, nous allons discuter brièvement comment la notion de symétrie intervient pour fonder ce type d’approche du réel. Prenons tout d’abord l’exemple du cadre classique. Une expérience peut être faite à différents moments, à différents endroits, et alors que l’expérimentateur est en déplacement (la terre, le soleil, la voie lactée bougent de toute façon...). Tout système de repérage comporte dès lors de l’arbitraire. La relativité galiléenne permet de surmonter cet arbitraire en proposant que tous les référentiels dits Galiléens sont symétriques, c’est-à-dire que les référentiels qui transforment un mouvement rectiligne uniforme en un autre sont équivalents. Ce type de mouvement constitue un état par défaut au sens où il est le mouvement de tout système lorsque rien n’agit sur lui^[15]. Ensuite interviennent les forces classiques qui vont précisément changer ce mouvement par l’équation : masse x accélération=somme des forces extérieures. Lorsqu’aucune force ne s’applique, l’accélération est nulle. Le mouvement inertiel (=rectiligne uniforme) est donc invariant par translation dans l’espace ou le temps, ou lorsqu’un déplacement uniforme est ajouté. Ces transformations sont donc des symétries, elles font partie des symétries de l’espace temps galiléen. Il est essentiel de comprendre que l’idée de relativité est que les mêmes équations fondamentales s’appliquent quel que soit le référentiel considéré, le passage d’un référentiel à l’autre forme alors des symétries de ces équations. Dans le cas galiléen, ce sera les mêmes forces (et donc la même accélération). Ceci permet de surmonter l’arbitraire des systèmes de référence sans avoir à évoquer un référentiel absolu (rien de connu ne permet de spécifier un tel référentiel objectivement). Cette symétrie entre référentiels galiléens joue donc un rôle crucial pour constituer l’espace temps de la physique classique et expliciter comment se joue la causalité et l’explication des phénomènes (par les forces). Notons au passage que l’état par défaut est celui où se produit le moins de changements possibles (le plus symétrique)^[16]. Einstein suit et prolonge très explicitement cette méthodologie lorsqu’il propose la relativité restreinte, qui conserve la vitesse de la lumière dans tous les référentiels (ce qui change profondément les notions d’espace et de temps). Regardons maintenant comment s’énonce la gravitation universelle de Newton. L’idée de newton est que tout objet, quel que soit sa composition, son histoire, sa vitesse, …, attire les autres objets proportionnellement à sa masse (et de manière inversement proportionnelle au carré de leurs distances^[17]). L’interaction physique s’applique de la même manière pour toute sorte de phénomènes ce qui permet de constituer un objet théorique traitable de manière générique sur le plan de la théorie, et s’appliquant à des objets concrets forts disparates par ailleurs (une pomme et une planète par exemple, nous évoquerons cependant plus loin la question de la chute des chats). Nous avons présenté les choses en termes d’application d’un même cadre à des phénomènes différents, mais notons qu’il est essentiel que le même raisonnement s’applique pour un même objet au cours du temps car c’est cela qui permet le calcul de sa trajectoire : l’objet suit la même détermination à chaque point de sa trajectoire ce qui rend possible son intelligibilité mathématique. Notons aussi que les principes de conservation physiques (énergie, moment, …), au cœur de ces calculs, sont explicitement reliés à des hypothèses de symétrie (du temps et de l’espace) par le théorème de Noether (et ses variantes)^[18]. Pour résumer la situation, nous avons un certain nombre de symétries théoriques que les équations vont respecter. Ces symétries vont permettre de justifier les équations utilisées pour décrire les phénomènes tout en définissant l’espace dans lequel se fait la description. Réciproquement l’écriture équationnelle implique certaines symétries (que les équations vérifient). Nous avons choisi des exemples relativement simples et anciens, mais cela est tout aussi valide pour les cadres les plus récents. Ainsi, la renormalisation utilisée en théorie quantique des champs et pour les phénomènes critiques se base fondamentalement sur le fait que des phénomènes à différentes échelles vont suivre les mêmes équations^[19] (en théorie quantique des champs, si une proposition théorique ne suit pas cette propriété, elle est mise à la corbeille... ce qui arrive en général lorsque l’on tente de comprendre la gravitation dans ce cadre). Le dernier point qu’il convient d’expliciter est que ces symétries et ces espaces permettent de déterminer la trajectoire de l’objet considéré (avec potentiellement un peu d’aléatoire). Du point de vue épistémologique, c’est bien évidemment cela qui va justifier l’ensemble de la construction conceptuelle et mathématique car cela permet la friction avec l’expérience. C’est en particulier parce que les objets génériques de la physique ont des trajectoires spécifiques dans leurs espaces de description que leurs définitions sont montrées comme pertinentes. Si la définition de l’objet ne permet pas de donner une telle détermination alors, il n’y a pas vraiment de raison de choisir cette définition plutôt qu’une autre. Les objets physiques sont donc fondamentalement des objets génériques, ce qui est au centre de leur mathématisation. Cette généricité est basée sur, et implique, des hypothèses de symétrie. Notons que l’allométrie, que nous avons discutée dans la partie précédente, procède de ce type de raisonnement, ainsi que la première partie de notre modélisation du temps biologique.

3.3 Changements de symétries en physique et criticité

Cette discussion n’exclue pas la présence de changements de symétrie dans les cadres physiques. Un cas particulièrement intéressant est celui des brisures spontanées de symétrie que nous discuterons dans le contexte des transitions de phase. Une transition de phase^[20] correspond typiquement à un changement radical du comportement et de la description d’un objet macroscopique, le passage de l’eau de l’état liquide à l’état de gaz ou de solide par exemple. Un autre exemple est celui de la transition paramagnétique-ferromagnétique : un métal tel que le fer n’est pas aimantable à haute température mais l’est à basse température. Nous avons insisté sur l’importance de la généricité de l’objet et de la présence de symétries pour leur mathématisation et leur description théorique, comment de tels changements sont-ils alors compris ? Pour saisir la situation, il faut bien distinguer la description microscopique et la description macroscopique de l’objet. Le niveau microscopique suit les mêmes équations dans les différents états macroscopiques et ces équations vérifient certaines symétries (par exemple pas d’aimantation privilégiée, ou pas de direction privilégiée dans l’espace). L’état microscopique correspondant respecte cette symétrie dans l’état désordonné (sans aimantation, gaz, …) mais ne la respecte plus dans l’état ordonné (système aimanté, solide). On dit alors que la symétrie est brisée. Notons que puisque les équations qui gouvernent le système sont symétriques, la manière dont la symétrie est brisée n’est pas donnée par elles, et est donc aléatoire. Par contre, au niveau macroscopique les choses sont différentes. Le passage à l’état ordonné s’accompagne de la nécessité d’introduire des variables supplémentaires : l’orientation d’un cristal, l’aimantation d’un aimant, … Ces quantités ne sont pas pertinentes dans la phase désordonnée. Nous voyons donc que la brisure de symétrie au niveau de la description microscopique s’accompagne de l’apparition de nouvelles quantités pertinentes au niveau macroscopique, mais aussi de l’introduction d’aléatoire. De manière générale, une brisure de symétrie, c’est-à-dire le passage d’un système vérifiant une symétrie tant au niveau de son état que de sa détermination, à une situation qui ne la vérifie pas implique l’introduction d’une quantité nouvelle, qui n’est pas donnée par la détermination théorique du système (puisque tout est initialement symétrique) et est donc aléatoire. Il est important d’ajouter ici que le comportement d’un système au point de transition, c’est-à-dire au point où se produit le changement de symétrie, est tout à fait particulier. De fait il a fallu attendre les années 1970 pour qu’un cadre d’intelligibilité soit proposé. Ce point, le point critique, se caractérise comme un entre deux, et en tant que tel ne correspond à aucun des états (ordonné et désordonné) qui l’avoisine, mais permet le passage de l’un à l’autre. Pour se faire, c’est-à-dire pour permettre l’apparition de nouvelles variables macroscopiques, un système met en place une structure de cohérence multi-échelle permettant que la plus petite perturbation conduise à l’apparition d’un ordre macroscopique. Ce type de situation est appelé critique.

4 Le cas des objets biologiques

4.1 Hypothèse

Le reste de notre discussion va se placer dans le cadre de la notion de criticité étendue^[21]. Plus précisément, nous discuterons ici l’idée suivante : toute transformation d’un objet biologique (organisme, cellule,...) peut s’accompagner d’un changement de symétrie non prédéfini. Cette hypothèse vise à appréhender la mise en place de l’organisation biologique et ses réorganisations, tant au cours du temps ontogénétique que phylogénétique. Il ne s’agit pas d’une hypothèse négative (bien qu’elle le soit du point de vue de la méthode) au sens où elle dit quelque chose sur la manière dont se comportent les objets biologiques. Ces changements peuvent être mis en évidence, et en tant que tels sont tout à fait observables. Nous allons montrer qu’elle permet de comprendre plusieurs notions propres à la biologie.

Mentionnons tout d’abord une conséquence immédiate. Nous avons discuté comment les symétries théoriques permettent d’établir l’espace de description pertinent, et comment une brisure de symétrie engendre l’apparition de nouvelles quantités pertinentes. Dès lors, l’hypothèse que nous avons formulée implique que l’espace de description change lorsque des transformations sont effectuées sur un objet considéré. Ceci s’applique en particulier aux transformations associées au passage du temps. Ces changements d’espace de description sont aléatoires au sens où ils correspondent à des changements de symétrie qui ne sont pas prédéfinis. Cet aléatoire est propre à la biologie, et n’existe pas dans les théories physiques existantes^[22]. Celles-ci comportent parfois des espaces de description pouvant changer, mais toujours sur la base de symétries prédéfinies, encadrant ces changements. Bien évidemment, notre discussion des changements d’espace de description pertinents implique directement la détermination théorique des objets étudiés (par exemple des équations), la pertinence de nouvelles variables, par exemple, provient précisément de leurs participations à cette détermination. Notons que des idées similaires ont été développées indépendamment par S. Kauffman^[23].

4.2 Les objets biologiques

Étant donné le rôle que les symétries jouent pour la constitution des objets en physique notre hypothèse n’est pas anodine. Elle implique des changements méthodologiques mais aussi une manière différente de penser les objets (en comparaison avec la physique). L’attitude physique consiste typiquement à penser l’objet comme ayant une détermination équationnelle stable, basée sur des symétries et des invariants correspondants, qu’il s’agit de mettre en évidence pour comprendre les phénomènes. C’est précisément cette stabilité qui est remise en cause lorsque l’on considère les organismes biologiques. Il ne s’agit pas pour autant de dire que les objets biologiques seraient dénués de stabilité, mais que le statut et le rôle de la stabilité est différent en biologie. Nous aborderons spécifiquement la question de la stabilité dans la section suivante. Nous pouvons maintenant caractériser certains aspects fondamentaux des objets biologiques. Ceux-ci ne peuvent pas être considérés comme des objets génériques comme en physique. Le passage du temps, en particulier, est associé à une succession de changements de symétrie, autrement dit de changements d’organisation. Partant de là, l’objet biologique prend un caractère spécifique, comme produit de cette histoire, et qui  diverge de la généricité des objets physiques. De manière duale, deux organismes aussi proches que possible auront néanmoins des différences qui ne se limitent pas à des différences quantitatives, mais qui, dès lors qu’elles se comprennent en termes de changements de symétrie, impliquent des différences de comportement. Ceci donne un sens physico-mathématique à la notion de variabilité. Ces deux notions, variabilité et historicité, sont couplées de manière fondamentale ici. L’historicité des objets biologiques est générée par la variabilité, mais elle ne s’y réduit pas strictement car cela supposerait de pouvoir faire la « somme » de la variabilité au cours de l’évolution, ce qui n’a pas vraiment de sens pratique, ni théorique dans le cadre où les changements de symétrie sont aléatoires. Remarquons ici l’homogénéité de notre cadre avec la théorie de l’évolution. En effet, sans diversification et apparition de nouveaux traits, l’évolution ne peut avoir lieu. De manière générale, la génétique des populations qui découple l’organisation des phénotypes des génotypes se base sur une méthodologie homogène à celle de la physique au sens où les traits et leurs propriétés sont pré-donnés dans les modèles, l’apparition de nouveaux traits et ses modalités est alors laissée dans l’ombre. Notre cadre vise en particulier à mettre ce genre de phénomènes en évidence. Nous avons mentionné le lien fondamental entre principes de conservation en physique et symétries théoriques. L’hypothèse que nous proposons peut donc être vue comme un principe de non-conservation. Du point de vue de la détermination des trajectoires, le couple objet générique – trajectoire spécifique qui fonctionne en physique est donc ici brisé, et dès lors que l’objet devient spécifique, les trajectoires ne peuvent plus être déterminées par la théorie comme la trajectoire suivie par le système, les trajectoires ne sont que des possibles. Notons néanmoins que ni la théorie classique des probabilités, ni la théorie quantique des probabilités ne conviennent pour décrire ces possibles car elles supposent toutes deux un ensemble des possibles qui soit prédéfini (de sorte que cet ensemble ait une probabilité de 1), et des symétries théoriques pour rendre objectives les probabilités assignées aux différents possibles (par exemple tous les états de même énergie sont considérés comme équivalents dans l’ensemble microcanonique de la physique statistique). L’hypothèse que nous proposons amène à devoir dépasser le concept de state determined system (Turing)^[24], c’est-à-dire l’idée qu’un objet peut être compris sur la base d’un état donné dans un espace, auquel s’ajoute une règle d’évolution (pour un système ayant une dynamique). Du point de vue classique, on essaierait de concevoir un organisme ou une cellule comme ayant un état dans un espace à très haute dimension. Une telle représentation est essentiellement fictionnelle en pratique, pose gravement le problème de son objectivité, mais nous semble de plus vaine au sens où le vivant se réorganise avec l’écoulement du temps, de sorte qu’elle ne saisirait pas cette propriété essentielle. Le point de vue que nous proposons a pour horizon de dépasser ces difficultés en changeant la manière de concevoir les objets biologiques et leur mathématisation pour produire un cadre cohérent pour la mathématisation de tel ou tel aspect étudié. Il ne s’agit pas de  se substituer à l’exploration de l’organisation du vivant dans sa complexité, mais de donner un cadre cohérent permettant de la discuter, tout en posant explicitement la question de l’étude du caractère labile de son organisation et, conjointement, la question de ses réorganisations. La notion de criticité, d’origine physique, est alors très pertinente car elle décrit un objet situé au moment d’un changement de son comportement. Le cadre que nous avons proposé pour la géométrie du temps des mammifères prouve par l’exemple que ce type de point de vue peut être fructueux. En effet, la discussion de la variabilité du rythme cardiaque part du principe que la détermination théorique d’une trajectoire individuelle n’est pas donnée (elle n’est donnée dans notre cadre que pour des moyennes très générales, telles que l’allométrie). Ceci permet d’injecter une trajectoire observée dans notre cadre et d’observer la manière dont la variabilité du rythme biologique par rapport au temps physique est organisée.

5 Stabilités chez le vivant

5.1 Les symétries comme contraintes

Comme nous l’avons mentionné plus tôt, l’hypothèse de la criticité étendue comme changements de symétries n’exclue pas que le vivant possède des éléments de stabilité. Au contraire l’idée de changements de symétries suppose que des symétries puissent être identifiées. Cependant les symétries proprement biologiques ne vont pas avoir le même rôle qu’en physique, en particulier parce qu’elles sont susceptibles de pouvoir changer avec l’avancé du temps biologique, de sorte que l’objet biologique, vu comme un objet physique change avec le temps. Les stabilités biologiques ont donc un caractère contingent qui diffère de la stabilité principielle des grandes symétries théoriques de la physique. Le changement de statut de l’objet en biologie (comme objet spécifique dont la trajectoire n’est pas déterminée théoriquement comme la trajectoire du système) implique que les objets déterminés par ces symétries, typiquement des parties d’un organisme ou d’une cellule, ne vont plus agir comme des causes au sens plein que ce terme peut avoir en physique (c’est-à-dire comme déterminant complètement la trajectoire, comme raison suffisante dirait-on en termes classiques) mais comme des contraintes. Les contraintes ont alors un double rôle d’ordre causal. Tout d’abord, elles canalisent les trajectoires biologiques, forçant de manière plus ou moins stricte certains comportements dès lors qu’un certain contexte est respecté (pour le reste de l’organisme et son environnement). Dans un même temps les contraintes ont aussi un rôle dans l’apparition de nouveaux possibles, imprédictibles, qui vont se baser sur leurs régularités pour se mettre en place. Prenons quelques exemples concrets. Comme nous l’avons discuté, le cycle jour-nuit est le produit d’invariances physiques et en tant que tel a une stabilité indépendante des phénomènes biologiques. Elle contraint certaines activités biologiques dépendantes de la lumière (et/ou de la température), telles que la photosynthèse ou la vision. Dans un même temps, cette stabilité rend possible un grand nombre de structures temporelles de l’activité biologique, conduisant par exemple à l’existence d’animaux diurnes, nocturnes, crépusculaires, … Dans le cadre que nous avons proposé, $\omega$e provient de l’invariance du rythme physique alors que Re  et surtout $\phi$ vont dépendre directement de la manière dont telle ou telle espèce (voire, dont tel ou tel individu) organise son activité par rapport à cet invariant physique. Notons cependant, qu’un rythme externe comme le rythme jour-nuit a été internalisé par les systèmes biologiques, par la formation d’activités rythmiques qui elles sont des contraintes proprement biologiques, pouvant être en décalage avec le rythme externe proprement physique. La notion de rythme circadien recouvre ces deux aspects. Un exemple assez proche est celui de la pesanteur. Celle-ci agit comme contrainte de manière uniforme tant sur l’évolution que sur les organismes. Lorsque cette contrainte est retirée, en microgravité, une désorganisation massive s’ensuit, ce qui explique les problèmes de santé associés à la présence dans l’espace^[25]. Bien évidemment, elle conduit aussi à une contrainte pour les déplacements des organismes. Les réponses biologiques à cette force physique, sont, par contre, diverses. Elles incluent la neutralisation de cette force par les vessies natatoires, où les ailes, l’apparition de la cellulose pour les plantes, la minéralisation des os en réponse à la pression exercée sur eux par le poids de l’animal, … Nous avons précédemment évoqué la question de la chute dans le champ de pesanteur dans les cadres purement physiques. Dans le cas d’un animal peu adapté au vol libre mais habitué aux hauteurs, le chat, et alors même que les forces physiques sont bien identifiées, l’incertitude sur la manière dont l’animal va changer de comportement au cours de la chute, laisse la question des conséquences d’une chute relativement ouverte a priori, et est le lieu de controverses^[26],^[27]. Nous avons pris deux exemples de contraintes externes aux organismes au sens où elles sont définies par des invariants physiques. Elles ne sont que partiellement externes car il convient de tenir compte du rôle joué par ces contraintes dans l’organisation biologique, et ce rôle, lui, est soumis à la variabilité et à l’historicité des objets biologiques. Bien évidemment ce concept s’applique aussi aux contraintes proprement biologiques, de fait nous proposons que les symétries utilisées dans les modèles de parties d’un organisme (qu’il s’agisse de modèles de leurs formations ou de leurs fonctionnements) ont le statut de contraintes. Ces contraintes ont une propriété particulière : elles sont dépendantes d’autres contraintes de l’organisme (pour leur formation et leurs maintiens). Cette idée est en lien direct avec les idées d’autopoïèse^[28], de clôture sous causes efficientes^[29] et plus généralement de clôture organisationnelle^[30], et nous l’avons développée avec beaucoup plus de détails ailleurs^[31]. Du point de vue pratique, pour une modélisation locale, elle implique que les hypothèses du modèle ne doivent pas être considérées comme des invariants du système, que l’on pourrait postuler comme tels, mais sont stabilisées par d’autres contraintes, et cette stabilisation peut être plus ou moins forte (ou stricte) suivant les cas, en particulier en fonction des modalités de cette stabilisation.

5.2 La mesure en biologie

La mesure a un sens précis (mais différent) dans chaque théorie physique. En mécanique classique (et plus généralement en physique classique), la mesure ne permet pas un accès parfait à l’état d’un système, mais seulement un accès imparfait, modélisé par un intervalle. Ceci permet l’intelligibilité des situations déterministes mais imprédictibles dans les cas de sensibilité aux conditions initiales telles que le chaos. En physique quantique, la mesure change l’état d’un système : l’état d’un électron peut être diffus dans l’espace mais dès lors que nous l’observons à un endroit alors il est bel et bien, et uniquement, à cet endroit (et n’est plus aussi ailleurs). Cette mesure est modélisée par un opérateur qui définit les résultats possibles et les états correspondants. C’est dans ce contexte quantique qu’Einstein fait la remarque suivante : « que l’on puisse observer une chose ou non dépend de la théorie que l’on utilise. C’est la théorie qui décide ce qui peut être observé »^[32]. En biologie, cette question n’a pratiquement pas été abordée comme question théorique majeure, malgré la richesse et l’originalité (par rapport aux autres disciplines) de la plupart des pratiques expérimentales. Notons l’exception de Rosen^[33], mais qui conserve un point de vue classique et discute la question du nombre d’observations nécessaires pour décrire un système classique. Remarquons tout de même que la biologie tend à utiliser la notion classique de mesure pour l’observation de variables continues. Notons aussi que pour ce qui est du séquençage d’ADN (et d’ARN), la notion de mesure associée est assez simple puisqu’un accès parfait est possible en principe, de par la structure discrète de l’objet considéré. Pourtant, et par contraste, l’expérimentation biologique a de très fortes spécificités par rapport à l’expérimentation physique. Nous proposons qu’en biologie l’observateur co-constitue les symétries théoriques permettant de décrire le phénomène considéré et son comportement. L’expérimentateur ne serait alors pas qu’un ``spectateur’’ (comme en physique classique) mais participerait à la détermination de l’objet (comme en physique quantique, mais de manière sensiblement différente). La modalité de cette participation est alors dans la mise en place de certaines régularités, ou plus techniquement dans l’établissement de certaines symétries. Cette notion de mesure intervient de manière pratique dans l’expérimentation, comme stabilisation de l’objet biologique permettant de lui donner une certaine généricité, suffisante en particulier pour la reproduction des résultats expérimentaux (lorsque ceux-ci sont effectivement reproductibles). De manière générale, cette symétrisation correspond au choix d’une histoire commune que les objets biologiques considérés possèdent. Déclinons les principaux aspects que prend cette symétrisation. Tout d’abord, une mesure biologique implique le choix d’un certain niveau de proximité phylogénétique. Cette proximité peut être plus ou moins forte suivant le phénomène étudié. Par exemple, les relations allométriques que nous avons discutées correspondent aux mammifères. Cependant la plupart des travaux expérimentaux utilisent des organismes ayant une proximité beaucoup plus grande. En utilisant une souche spécifique par exemple, voire en microbiologie ou en biologie cellulaire, une population issue d’une seule cellule. Il est important de comprendre que ce point a deux rôles. Il vise certes à réduire la variabilité, mais surtout il est une conséquence, dans la pratique expérimentale, de la spécificité de l’objet biologique. N’étant pas défini comme objet générique, par des symétries théoriques, l’objet biologique, théorique et expérimental, est toujours défini, au moins en partie, par référence à sa généalogie. Lorsque cela est possible, les organismes objets de l’expérimentation sont mis dans des conditions similaires pendant un certain temps. Par exemple, des cellules sont mises dans des conditions permettant une prolifération exponentielle pendant plusieurs semaines avant une expérimentation in vitro, de sorte qu’elles ne se contraignent pas (ou peu) mutuellement de manière spécifique. Ce point permet d’assurer que les objets ont une histoire récente commune, au-delà de la phylogénie et réduit donc la variabilité entre les expériences. Enfin, et bien évidemment, les conditions expérimentales elles-mêmes sont choisies pour produire une certaine généricité des comportements biologiques (et donc limiter la variabilité). Ajoutons que même lorsque le choix d’un protocole expérimental contraint fortement l’objet étudié, la variabilité reste une composante irréductible de la détermination des objets étudiés. Si l’on reprend l’exemple de l’allométrie, la mesure consiste essentiellement à choisir un niveau phylogénétique (les mammifères par exemple) et à contraindre les organismes observés de manière à réduire les spécificités de telle ou telle espèce. Ceci est obtenu par le choix du métabolisme basal. Ce dernier correspond à un état de veille et exclut toute activité particulière (digestion, locomotion,...). Un autre type d’activité permet d’obtenir une grande régularité, il s’agit du métabolisme maximum (le niveau maximum d’activité soutenable). Même dans ces conditions, la variabilité reste forte, tant pour les individus que pour les espèces. Dans notre approche, la notion de mesure part donc directement de l’historicité et de la contextualité des objets biologiques, et correspond aux pratiques expérimentales tout en les réinterprétant. La mesure n’est alors pas un simple accès à un objet qui serait préexistant, avec ses symétries et invariants, mais participe à les définir comme tels.

6 Conclusion

1. Les propositions que nous esquissons dans ce texte conduisent à reconsidérer la manière d’aborder les objets biologiques, en particulier dès lors que se pose le problème de leur mathématisation. Les théories physiques parviennent à comprendre de nombreux phénomènes de manière anhistorique, ce qui correspond à la spontanéité expérimentale de ces phénomènes. En principe, même les situations suivant de peu le big bang peuvent être retrouvées par l’obtention de niveaux d’énergie très élevés (dans les accélérateurs de particules). En biologie, au contraire, les exemples montrant que la compréhension de tel ou tel trait est d’ordre évolutive sont innombrables. Or cela signifie qu’ils ne sont pas compris comme optimisation d’une fonctionnelle correspondant à la situation présente, ou même à un phénomène de relaxation comme en thermodynamique loin de l’équilibre.
2. Du point de vue de la pensée physico-mathématique se pose alors fondamentalement la question de la méthode pour appréhender de telles situations, et en particulier la question de savoir comment comprendre des systèmes qui ne soient pas déterminés par leurs états (la notion d’état étant basée sur l’hypothèse d’un espace prédéfini, donc de symétries stables). Nous avons discuté quelques pistes, basées sur l’idée que la stabilité de tel ou tel aspect d’un objet biologique peut être appréhendée comme une contrainte, et est en particulier stabilisée par le reste de l’organisation biologique.

Références

1. 1. F. Bailly et G.  Longo, Mathematics and the natural sciences ; the physical singularity of life, Imperial College Press, London, 2011, version préliminaire en franç ais : Hermann, Vision des sciences, 2006.
2. 2. F. Bailly, G. Longo et M.  Montévil – «  A 2-dimensional geometry for biological time   », Progress in Biophysics and MolecularBiology 106 (2011), no. 3, p. 474 – 484.
3. 3. M. Rubner – « ü ber den Einfluss der Körpergrösse auf Stoff- und Kraftwechsel », Zeitschrift fiir Biologie 19 (1883), p. 535–562.
4. 4. P.S. Agutter et D.N. Wheatley – « Metabolic scaling : Consensus or controversy ? », Theoretical Biology and Medical Modelling 1 (2004), p.  13.
5. 5. Chapitre 2, G. Longo et M. Montévil – Perspectives on organisms : Biological time, symmetries and singularities, Lecture Notes in Morphogenesis, Springer, 2014.
6. 6. G.B. West, J.H. Brown et B.J. Enquist – « The fourth dimension of life : Fractal geometry and allometric scaling of organisms », Science 284 (1999), no.  5420, p. 1677–1679.
7. 7. S.L. Lindstedt et W.A. Calder III – « Body size, physiological time, and longevity of homeothermic animals », Quarterly Review of Biology (1981), p.  1–16.
8. 8. F. Bailly, G. Longo et M.  Montévil – « A 2-dimensional geometry for biological time », Progress in Biophysics and Molecular Biology 106 (2011), no. 3, p. 474 – 484.
9. 9. Chapitre 3 G. Longo et M. Montévil – Perspectives on organisms : Biological time, symmetries and singularities, Lecture Notes in Morphogenesis, Springer, 2014.
10. 10. Chapitre 2 G. Longo et M. Montévil – Perspectives on organisms : Biological time, symmetries and singularities, Lecture Notes in Morphogenesis, Springer, 2014.
11. 11. B.J. West – Where medicine went wrong : Rediscovering the path to complexity, vol. Volume 11 of Studies of nonlinear phenomena in life sciences, World Scientific, Teaneck, NJ, 2006.
12. 12. G. Longo et M. Montévil – Perspectives on organisms : Biological time, symmetries and singularities, Lecture Notes in Morphogenesis, Springer, 2014.
13. 13. B.C. Van Fraassen – Laws and symmetry, Oxford University Press, USA, 1989.
14. 14. F. Bailly et G.  Longo –Mathematics and the natural sciences ; the physical singularity of life, Imperial College Press, London, 2011, Preliminary version in French : Hermann, Vision des sciences, 2006.
15. 15. G. Longo, M. Montévil, C. Sonnenschein et A. M. Soto – « In search of principles for a theory of organisms », Bioessays (submitted).
16. 16. L’immobilité est relative car elle d épend du réfé rentiel, alors que le mouvement rectiligne uniforme ne comporte que des changements imposé par la relativité galiléenne.
17. 17. Cet exposant n’est pas anodin, il permet notamment d’identifier un objet é tendu dans l’espace avec son centre de gravité.
18. 18. Y. Kosmann-Schwarzbach – Les thé orèmes de noether : invariance et lois de conservation au xxe si ècle, Editions Ecole Polytechnique, 2004.
19. 19. J.  Zinn-Justin – Phase transitions and renormalization group, Oxford University Press, New York, 2007.
20. 20. J.  Binney, N.J. Dowrick, A.J. Fisher et M.E.J. Newman – The theory of critical phenomena : An introduction to the renormalization group., Oxford U. P., 1992.
21. 21. G. Longo et M. Montévil – Perspectives on organisms : Biological time, symmetries and singularities, Lecture Notes in Morphogenesis, Springer, 2014.
22. 22. G. Longo et M Montévil – « Extended criticality, phase spaces and enablement in biology », Chaos, Solitons & Fractals (2013).
23. 23. S.A. Kauffman – Investigations, Oxford University Press, USA, 2002.
24. 24. A. M Turing – « Computing machinery and intelligence », Mind 59 (1950), no.  236, p. 433–460.
25. 25. M. Bizzarri, A. Cucina, A.  Palombo et M. G. Masiello – « Gravity sensing by cells : mechanisms and theoretical grounds », Rendiconti Lincei 25 (2014), no. 1, p. 29–38.
26. 26. WO Whitney et CJ  Mehlhaff – « High-rise syndrome in cats. », Journal of the American Veterinary Medical Association 191 (1987), no. 11, p.  1399–1403.
27. 27. Dražen Vnuk, Boris Pirki ć, Dražen Matiči ć, Berislav Radišić, Marko Stejskal, Tomislav Babić, Mario Kreszinger et Nikš a Lemo – « Feline high-rise syndrome : 119 cases (1998–2001) », Journal of Feline Medicine & Surgery 6 (2004), no. 5, p.  305–312.
28. 28. F.J. Varela – Principles of biological autonomy, North Holland New York, 1979.
29. 29. R. Rosen – Life itself : a comprehensive inquiry into the nature, origin, and fabrication of life, Columbia U. P., 1991.
30. 30. M Mossio et A  Moreno – « Organisational closure in biological organisms. », History and philosophy of the life sciences 32 (2010), no.  2-3, p. 269–288.
31. 31. M. Montévil et M.  Mossio – "Closure of constraints in biological organisation", (2014), To be submitted.
32. 32. A. Salam – Unification of fundamental forces, Cambridge University Press, 1990.
33. 33. R.  Rosen – « Observation and biological systems », Bulletin of Mathematical Biology 39 (1977), no. 6, p.  663 – 678.