Repetition and reversibility in evolution: Theoretical population genetics: Philosophical perspectives of time in natural sciences
Time of nature and the nature of time: Philosophical perspectives of time in natural sciences
We analyze repetitiveness, reversibility and irreversibility in theoretical population genetics and disentangle concepts that are often confused.
Abstract
Repetitiveness and reversibility have long been considered as characteristic features of scientific knowledge. In theoretical population genetics, repetitiveness is illustrated by a number of genetic equilibria realized under specific conditions. Since these equilibria are maintained despite a continual flux of changes in the course of generations (reshuffling of genes, reproduction…), it can legitimately be said that population genetics reveals important properties of invariance through transformation. Time-reversibility is a more controversial subject. Here, the parallel with classical mechanics is much weaker. Time-reversibility is unquestionable in some stochastic models, but at the cost of a special, probabilistic concept of reversibility. But it does not seem to be a property of the most basic deterministic models describing the dynamics of evolutionary change at the level of populations and genes. Furthermore, various meanings of “reversibility” are distinguished. In particular, time-reversibility should not be confused with retrodictability.
Keywords: population genetics, repetition, retrodiction, reversibility
Traduction abrégée en Français.
Table of contents
Reading time: ~105 min
- 1. Introduction
- 2. Repetitiveness in theoretical population genetics
- 3. Time-reversibility
- 4. Conclusions
- Appendices
- 1. Time reversibility
- 2. Application to models of population genetics
- 3. Figures 3, 4, 5, 6 and 7
- References
Chapter 12 - Repetition and Reversibility in Evolution: Theoretical Population Genetics
∗ Université Paris I Panthéon-Sorbonne
† Université Paris 7 Diderot
Abstract
Repetitiveness and reversibility have long been considered as characteristic features of scientific knowledge. In theoretical population genetics, repetitiveness is illustrated by a number of genetic equilibria realized under specific conditions. Since these equilibria are maintained despite a continual flux of changes in the course of generations (reshuffling of genes, reproduction…), it can legitimately be said that population genetics reveals important properties of invariance through transformation. Time-reversibility is a more controversial subject. Here, the parallel with classical mechanics is much weaker. Time-reversibility is unquestionable in some stochastic models, but at the cost of a special, probabilistic concept of reversibility. But it does not seem to be a property of the most basic deterministic models describing the dynamics of evolutionary change at the level of populations and genes. Furthermore, various meanings of ‘reversibility’ are distinguished. In particular, time-reversibility should not be confused with retrodictability.
1. Introduction
Evolutionary biologists commonly assume that “evolution is unique and irreversible”. In contemporary literature, this claim is often closely related to the claim that evolution is historically contingent from top to bottom with no laws and no genuine theories. Although the authors share John Beatty’s assertion that all (or almost all) biological generalizations are ultimately historically contingent[2] , they believe that the phrase “evolution is unique and irreversible” is far too general and too vague to be plausible. In reality, contemporary biology offers significant examples of repetition, invariance, and reversibility, both at the theoretical and the experimental level. Such examples may help to get out of the too-narrow alternative between “historical contingency” and “lawfulness” in biology, and particularly in evolutionary biology. In a sense, this alternative suffers from its excessive philosophical radicalness. The issues of repeatability vs. non-repeatability and reversibility vs. irreversibility of evolutionary phenomena offer a useful tool to make the debate more nuanced. It may be the case that repeatability and reversibility in evolution are marginal; nevertheless there are clear cases, both at the theoretical and the experimental level. The present paper will concentrate exclusively on theoretical population genetics.[3]
What exactly do the terms “repeatability” and “reversibility” mean? The definition is a delicate issue here, especially for the second notion. Does reversibility in evolution mean that an evolving entity (e.g. a population or a species) can return to a previous state (whatever the trajectory), or that the reverse trajectory should be strictly symmetrical with the direct trajectory? In his papers on the irreversibility of evolution, the Belgian Palaeontologist Louis Dollo was particularly concerned by this latter sense of “reversibility”: “In order for [evolution] to be reversible, we would have to admit the intervention of causes exactly inverse to those which gave rise to the individual variations which were the source of the first transformation and also to their fixation in an exactly inverse order” (Dollo 1913, quoted in Gould 1970, p. 199). Another difficulty arises from the technical notions of reversibility used in mathematics and physics. Do these notions apply to evolutionary biology? One of the main objectives of this chapter is to clarify the varying meanings of repetition and reversibility applicable to evolution. Repetition is a simpler matter, but this notion also involves a certain amount of ambiguity. Indeed, the two notions of repetition and reversibility should not be conflated as George Gaylord Simpson did when he commented on Dollo: “… evolution is a special case of the fact that history does not repeat itself. The fossil record and the evolutionary sequences that it illustrates are historical in nature, and history is inherently irreversible” (Simpson 1964, p. 196; quoted in Gould 1970, p. 208-209). Simpson’s statement seems a little too obvious. Although evolutionary reversibility is most often related to the kind of repetition that is so important for living beings—reproduction—repetition and reversibility should be clearly distinguished from one another.
When Louis Dollo introduced his famous “law of irreversibility in evolution”, he defined it in the following terms: “… an organism cannot return, even partially, to a former state already realized in the series of its ancestors.” (Dollo 1893, translated by Gould 1970, p. 211). As suggested by this formula, Dollo was interested in the problem of reversibility be it at the level of the organism or at least of a complex organ. Furthermore, as a palaeontologist, he conceived his “law” as applying to a large temporal scale (macroevolution in modern terms). Dollo did not deny that reversion could occur at more elementary levels. Moreover, neither genetics nor even less population genetics, existed when Dollo proposed his law of irreversibility in evolution. Therefore, and in view of present knowledge, it seems appropriate to reassess the problems of invariance and reversibility at a microevolutionary level.
Repetitiveness and reversibility in evolution can be assessed at two different levels, empirical and theoretical. At an empirical level, living objects exhibit properties of invariance that are crucial for evolutionary change. Current examples of invariance include gene replication and constancy of the number of chromosomes in the process of cell reproduction; and reproduction and alternate generations at organism level. In such cases, invariance is not absolute, indeed the replication of genetic material is not always perfect; correlatively, hereditary material exhibits an ability to change (genic mutations, recombination, chromosomal accidents…). Similarly, reproduction can encounter accidents (e.g. developmental anomalies), and exists under various modes (e.g. asexual vs. sexual reproduction, diverse schemas of alternate generations). Replication and reproduction are very general properties of living beings, and provide a basis for evolutionary models. They objectively exist throughout the living world. Of course, they result from a historical process, and for that reason, they cannot be thought of in terms of “laws of nature” in the sense of universal statements of unlimited scope, applying everywhere and at any time in the universe. One of us advocates the use of the concept of constraints in order to discuss limited invariance in the context of biological historicity (Longo and Montévil 2014, Montévil and Mossio 2015).
Population geneticists also share an intuitive notion of reversibility. Some biological processes make the return of a population to a previous state possible. Obvious examples include reverse mutation, especially if repeated; backwards selection (i.e. inverted selection coefficients); and chance (random drift). What “reversibility” precisely means in these examples is open to question, however the idea that populations can return to a previous state is perfectly plausible, given the nature of the basic biological processes involved in genetic evolution. There is another manner of formulating the intuitive notion of reversible evolution, which is more precise and better adapted to present genetic knowledge, namely: “for a given individual, consider the set of all its possible genetic states. One can move from one state to another thanks to the ordinary sources of genetic change (substitution of nucleotides, deletion, insertion, recombination, etc.). It is obvious that any sequence of states E1, E2… Ei… Ek that an individual can follow can also be followed in the reverse direction.” (Goux 1979, p. 568, our translation).
These intuitive notions of repetitiveness and reversibility come prior to the construction of models in population genetics. They should be carefully distinguished from the properties discovered through the development of theoretical models describing the genetic evolution of populations. At that theoretical level, non-trivial notions of repetitiveness and reversibility occur; they result from modelling itself. Section 2 shows how population genetics models satisfies a characteristic feature of scientific knowledge currently found in the physical sciences, namely the discovery of formal properties of invariance through transformation. The next section examines whether theoretical genetics has also the capacity of discovering properties of reversibility or not. This is a more difficult issue. After defining several possible meanings of reversibility, section 3 shows that time reversibility in the mathematical sense is illustrated by some stochastic models, whereas basic deterministic models do not exhibit the property of time-reversibility. The concluding section raises serious doubts about the traditional comparison made between classical mechanics and the deterministic models of population genetics.
2. Repetitiveness in theoretical population genetics
Jean-Michel Goux observes that the source of a number of equilibria in population genetics is the endless repetitiveness of the life cycle (1979, p. 567). We will here freely expand on this proposal. In spite of its sophisticated use in mathematics, the notion of invariance under transformation can be defined in a simple and general way, and can be applied to many different areas of knowledge, not only in mathematics and theoretical physics. For a given class of objects, an invariant is a property that remains unchanged when a specified type of transformation is applied to the objects. This concept is especially fruitful when the objects and their relations are described by mathematical formulae; in such cases, a precise sense can be given to what is said to be invariant.
One of the most famous examples of invariance to transformation in physics is the Galilean transformation. In its traditional formulation in classical mechanics, Galileo’s principle of invariance (also called Galileo’s principle of relativity) states that the laws of motion are the same in all inertial frames. Based on the postulate of absolute time and absolute metric of space, this principle makes the transformation of spatial and temporal coordinates from one inertial referential system to another possible. For instance, if the speed of material point in S is v, its speed in S’ will be[4] :
Vx’ i = dx’/dt = d(x-vt)/dt = vx - v
Invariants through transformation may be of many kinds. In classical and relativist mechanics they are relative to motion. However they can also be relative to structures (i.e. the composition of a particular class of objects). This section considers the case of invariance relative to the genetic structure of a population in specified conditions. Some classic examples of genetic equilibria are given below, which all belong to what could be called evolutionary statics, as opposed to evolutionary dynamics. Time-reversibility is also an extreme case of invariance through transformation. This notion will be considered in section 3, devoted to evolutionary dynamics in population genetics.
The Hardy and Weinberg equilibrium is certainly the best-known example of a structural invariant. Consider a single locus with two alleles A and a with frequencies p and q (with p + q = 1)[5] . The Hardy and Weinberg law states that, irrespective of the initial gene frequencies and the initial genotype frequencies, if [1] all crosses occur within the same generation (no overlapping generations), if there is [2] no selection, [3] no migration, [4] no mutation, if [5] mating is random, and if [6] if the population size N is big enough to consider that 1/N ≈ 0, then the genotypic frequencies are constant and depend only on the gene frequency of the initial generation (for a precise formulation of these conditions, see Jacquard 1971, p. 48-58, and Hartl, 1980, pp. 93-94). Under such conditions, the expected genotypic ratios are AA : p2 ; Aa : 2pq ; aa : q2. In a discrete-generation population, the population immediately achieves these proportions from the first generation of mating, and the expected ratios remain constant as long as the six conditions mentioned are satisfied. The Hardy and Weinberg [HW] law derives its name from the British mathematician G. H. Hardy[6] (1877-1947) and the German physician and obstetrician Wilhelm Weinberg (1835-1937), who independently and simultaneously demonstrated it in 1908 (Hardy 1908; Weinberg 1908). Some authors call it a ‘principle’ (Crow and Kimura 1970). But it is more accurately characterized as a theorem, because it can be demonstrated on the mere basis of the Mendelian law of segregation and the six conditions stated above. It is also commonly referred to as “the Hardy-Weinberg equilibrium”, where “equilibrium [refers] to the fact that there is no tendency for the variation caused by the co-existence of different genotypes to disappear” (Edwards 1977, p. 7). The reason why this law is so important is that it purely expresses the effect of Mendelian inheritance in the absence of any factor able to change the genetic frequencies (i.e. gene frequencies and genotypic frequencies)[7]. As Edwards puts it, “this ability to maintain genetic variation is one of the most important aspects of Mendelian genetics” ( ibid.). The constancy of genetic frequencies under Mendelian inheritance provides a reference model for describing the effects of evolutionary “forces”, especially mutation, migration, selection, population size, inbreeding, and the mating system (homogamy vs. heterogamy), which may modify the genotypic structure of the population[8] . Returning to the problem of repetitiveness, the HW equilibrium is typically an invariant under transformation, because it identifies something (the distribution of gene and genotypic frequencies) that persists in spite of the indefinite reshuffling of the alleles that meiosis dissociates at each generation. Of course, the HW law is an idealization, because no real population ever strictly satisfies the conditions that permit its derivation.
Another classic example of structural invariance under transformation in population genetics is “Wright’s principle”, also called “Wright’s law of equilibrium”. This gives the frequency distribution of genotypes in an infinite population, for a diallelic locus[9] :
(p2+Fpq) + 2 pq(1-F) + (q2+F pq) = 1
where F is the coefficient of inbreeding. This law expresses the zygotic proportions[10] expected in a population with a certain amount of inbreeding, in other words a population where mates are more closely related than if they were chosen at random. The Hardy-Weinberg equilibrium is in fact a particular case of Wright’s equilibrium, corresponding to F=0. Therefore, Wright’s law of equilibrium takes into account one of the major causes of departure from the HW equilibrium (the other one being assortative mating). The F coefficient may of course change. Nevertheless, Wright’s formula states that for a given F, and if no other factor is allowed to modify the genotypic frequencies, the genetic structure of the population is invariant from generation to generation. Apart from the Hardy and Weinberg law and Fisher’s 1918 paper on the correlation between relatives under Mendelian Inheritance (Fisher 1918), this is one of the oldest results in theoretical population genetics. It has been demonstrated several times, and improved and generalized (multi-allelism) since Wright’s original paper in 1921 (Wright 1921; Malécot 1948; Li 1955).
As said earlier, the Hardy and Weinberg equilibrium is established as early as the first generation of crossing (the first zygotes made from the previous generation). But this is true only if generations do not overlap (see above: condition 1). If generations overlap, it takes more time for the HW equilibrium (as well as Wright’s equilibrium) to be established, but the population does converge towards this equilibrium. Therefore, the equilibrium does not emerge immediately, as in the discrete case, but gradually, as what could be described as a “trend”.
This notion of “trend”, which is very ubiquitous in theoretical population genetics, leads to an important remark about equilibria in this discipline. The search for equilibria is an important part of theoretical population genetics. Developing an idea suggested by J. B. S. Haldane, Crow and Kimura speak of “evolutionary statics”, as opposed to “the dynamics of evolution”. In a paper entitled “The Statics of Evolution”, Haldane (1954) declared that, in spite of evolution being a “dynamical process”, a good deal of it is better understood in terms of “statics”. Haldane stated that the reason for this was that evolution is usually an extremely slow process, which may, nevertheless, rely upon strong forces (esp. selection). Whence the idea that an important part of evolutionary processes should be thought of in terms of “approximate equilibria” resulting from a balance of ‘forces’ that quite often conflict with each other (e.g. various kinds of selection, selection and migration, selection and mutation, etc.), and that result in the persistence genetic polymorphism. The ‘statics’ of evolution is indeed one of the most spectacular parts of theoretical population genetics. Quite often, the results are simple, elegant and easily found, in contrast to the difficulty associated with the mathematical treatment of the ‘dynamics’ (which will be evoked in the next section, when coming to ‘reversibility’). For this reason, equilibrium formulae play an important role in the elementary teaching of population genetics.
In their Introduction to Population Genetics Theory (1970), Crow and Kimura devote an entire chapter to “Populations in approximate equilibrium” (Chap. 6). They examine an impressive list of factors maintaining gene frequency equilibria. All these factors “depend on some kind of balance between opposing forces” (Crow and Kimura 1970, p. 256). A partial list of the types of such equilibria is given below (from Crow and Kimura 1970, p. 256-196). Quite often, the models obtained are simple. Illustrative examples are given for the first two categories in the list.
-
Equilibrium between selection and mutation. For instance, in the case of a single locus with complete dominance where the recessive homozygous-mutant genotype is disadvantaged, and where mating is random, the equilibrium is reached when
with q: frequency of the mutant gene; u: mutation rate; s: selection coefficient.
-
Equilibrium under mutation pressure (infinite population, no random drift). For instance, in the simple case of a two-way recurrent mutation, the equilibrium is reached when
-
Equilibrium between migration and random drift.
-
Equilibrium under selection: stabilizing selection (selection directed towards the elimination of deviants)[11] , advantage to the heterozygote[12] , frequency dependent selection[13] , disruptive selection (selection in varying directions), multi-niche polymorphism…
-
Selective models accounting for the constancy of sex ratio (most often 1:1 at the age of reproduction).
All these equilibria—and this list is not exhaustive—isolate an invariant under transformation. For instance, the model for a two-way recurrent mutation tells us how the genetic structure of a population (both gene frequencies and genotypic frequencies) is preserved as long as the same conditions hold. In spite of the endless reshuffling of genes and of changes recurrently caused by two mutation pressures, an equilibrium is attained. Despite the obvious complexity and historicity of evolutionary phenomena, equilibrium models reveal invariant relations between parameters (gene and genotypic frequencies, mutation rates, selection rates, etc.) under idealized conditions.
The discovery of formal properties of invariance through transformation is an important component of scientific knowledge, whether in biology, physics or economics. In his Models of Discovery, Herbert Simon once wrote that “the notion of invariance under transformation as a necessary condition for a ‘real’ property of a physical system has provided a leading motivation for the development of relativistic mechanics and other branches of physics” (Simon 1977, p. 79, n. 8). We should not be surprised to find such invariants in evolutionary theory. As previously stated, repetitiveness is a massive empirical property of living beings: repetitiveness of life cycles, repetitiveness of cellular reproduction, repetitiveness of gene replication, and also repetitiveness of occasional phenomena such as recurrent mutation at population level. Given that repetitive phenomena are so widely observed at an elementary level, it is reasonable to expect that more formal invariants emerge when population genetics extrapolates from these empirical cases of repetitiveness to the behaviour of populations. As suggested in the introduction, the huge degree of historicity and contingency in evolution should not dismiss a certain amount of lawfulness, at least at the microevolutionary level.
3. Time-reversibility
Time reversibility is a less obvious notion than invariance through transformation, for two reasons. First, it refers to problems that may become highly technical, and counter-intuitive in terms of their mathematical treatment. Secondly, evolutionary biologists use different notions of reversibility, and very often they do this unconsciously. Discussing time reversibility with several population geneticists, we have been struck by the combination of spontaneous certainty and doubt manifested in their spontaneous reactions to this subject. One of the most common reactions was: “yes, obviously, the deterministic models (esp. models of selection) are reversible, but, if random drift is taken into account, the opposite is true… Markovian processes are deprived of memory…”. Another rarer response was: “Most probably, the equations describing the effect of deterministic processes do not describe reversible processes, but it seems evident that there is a large amount of reversibility in the models describing stochastic events”. Such contradictory statements, made by some renowned population geneticists, triggered our curiosity. But the most common thought was of the following type: “obviously” the biological processes involved in the evolution of a population may “in principle” cause the return of the population to a previous state. For instance, if a mutant allele gets fixed, there is always the possibility that a reverse mutation will trigger a reverse evolution (through the accumulation of such mutations, or appropriate selective pressure, or random drift). Similarly, if the hierarchy of selective pressures is inverted, then reverse evolution will follow[14] . In fact, it seems that population geneticists, although excited by the problem, do not have a clear and articulate position. They use the word to have various meanings. This section intends to clarify the several possible meanings of ‘reversibility’ with respect to population genetics.
Three different senses of ‘reversibility’ can be found in the current—mainly mathematical and physical—scientific literature. After giving definitions for these, the level of their applicability to population genetics will be considered and the less conventional and specifically biological meanings of ‘reversibility’ among population geneticists will be discussed.
3.1 Three senses of ‘reversibility’
To correctly treat reversibility as an operational concept in mathematics, physics and other exact sciences, would require a more formal and detailed analysis. The remarks that follow will only sketch out some distinctions that may help clarify the problem of reversibility in population genetics[15] .
3.1.1 Retrodictability
In classical mechanics, prediction and retrodiction are symmetrical: knowing the law(s) governing the development of a certain phenomenon through time and the state of the system at a given time t, it is possible to infer the state of the system at any other time, past or future. For instance, given Kepler’s laws for the motion of the planets in the solar system, and given appropriate information about the state of a planet a time t (that is the position and instantaneous speed of the planet considered, as well as of other planets that interact with it), the position and speed of this planet at any past or future time can be inferred. What is required for retrodictability is the possibility of deriving a backward equation from the forward equation that describes the past trajectory as precisely as the forward equation describes the normal motion. For such an inference, the astronomer’s theoretical framework does not need to be perfect. It may have, and certainly has its own limits (for instance Poincaré’s three bodies problem). We just assume a certain more or less sophisticated theoretical system, describing a deterministic process. If the process is deterministic, prediction and retrodiction are expected to be equally possible; note also that, in discrete time, retrodictibility may sometimes be impossible for deterministic systems (see Appendix 1). Retrodictability is often associated and identified with time reversibility in the mathematical sense (see below, [2]), and the two notions may indeed be closely related in particular cases. But as will be seen shortly, they are distinct. Because of the confusions resulting from equating retrodictability and reversibility, speaking of retrodiction (inference to the past) as a case of ‘reversibility’ should definitely be avoided. Although not common usage, the rest of this paper will repeatedly distinguish ‘time-reversibility’ (reversibility sensu stricto) and retrodictability.
3.1.2 Time reversibility in the conventional ‘mathematical’ sense
The notion of time-reversibility is based on a comparison between normal trajectories and trajectories after time reversal, that is to say where the past becomes the future and the future becomes the past. Reversibility occurs when these two trajectories follow the same law. Conversely, when the dynamics are irreversible, the law provides an orientation to time (the ‘arrow of time’). The question of time-reversibility in this sense is commonly discussed in theoretical physics, see for example chapter 7 and 8.
From a technical point of view, a time-reversible process is such that the equations describing its dynamics are invariant if the sign of time is reversed. In other words, if ‘-t’ is substituted for ‘t’, the law(s) governing the phenomenon is unaffected. In the case of classical mechanics, this will usually be checked by looking at the second order derivative of the equation describing the trajectory of the system. Consider for instance Galileo’s law of falling bodies, which states that the distance x travelled by a free-falling body is directly proportional to the square of the time t for which it falls: x= 1/2 gt2. The first order derivative, dx/dt = gt gives the speed. The second order derivative, d2 x/dt2 = g gives the acceleration, which is the key element from a dynamic point of view. It is easily seen that substituting –t for t in this second order derivative does not change anything. The same ‘law’ holds in both time-directions. This means that, if a ball is thrown up, the law governing the motion of the rising ball is identical to the law that describes the motion of the falling ball (not similar, but identical). The direction of the trajectory will be inverted, of course, and the speed will diminish instead of increasing, but the rate of the decrease will be strictly the same as the rate of the increase: the dynamics governing the process is the same. This is exactly what the second order derivative says: since t exists only as a square number in d2x/dt2 = g, this equation is not affected by an inversion of time. The transition from t to t+1 and the transition from t+1 to t are said to follow the same ‘law’. Indeed, this insensitivity can be demonstrated for both a discretized formulation of Galileo’s law (where the evolution of the system is described at successive discrete steps, t, t+1, etc.) and for continuous time (that is using a differential equation). In this precise sense, time reversibility is traditionally seen as an almost universal property of the laws of classical mechanics. In this respect, the best examples of time-reversibility (T-symmetry) are to be found in the fundamental laws of mechanics, which give the basic dynamics underlying mechanical processes. Newton’s law expressing the relationship between force and acceleration (F = ma) would certainly be a better example than Galileo’s law, an empirical law describing a trajectory rather than genuine dynamics. It is easy to understand that d2x/dt2 = F(x)/m holds also after time reversal. With Newton’s law, there is no need to be concerned with the counter-intuitive representations associated with a falling body governed by the same law both when it falls and when it is ‘thrown up’, or ‘reverts’ (when, how, what initial conditions, etc.—all elements that are unclear in the example). It should be noted, however, that Newton’s law, F = ma, is time-reversible if and only if F is symmetrical by time-reversal (see Appendix 1.1 for a more formal definition), for example when F depends only on x. This is the case for all classical fundamental forces, gravitation and electromagnetism. However, in other cases such as friction, where F = –fdx/dt (where f is the friction coefficient), the law is no longer reversible.
The relation between reversibility and retrodictability is a delicate problem. The two notions may be closely related in particular cases. For instance, Galileo’s law discussed above, allows for both retrodictability and reversibility. Knowing the position and the speed of a material point at any instant enables the prediction of the future and of the past position and speed of this material point at any time (within the limits of the actual trajectory). But Galileo’s law also satisfies the condition of reversibility: it describes a transformation in both possible directions. However, the two notions are not necessarily associated. Consider the case of discrete time equations, which are particularly important in population genetics. The function g allowing a ‘prediction of the past’ may be totally different from the function that describes how the system passes from t to t+1. Now consider a recurrence equation of the form p( t+1) = g[p(t)]. Reversibility means:
| p(t+1) = g[p( t)] → p(t) = g[ p(t+1)] | [1] |
with p designating some function of time, and g the function defining the dynamic of p ( i.e. what future state follows from the current state).
This formula means that the transition from t to t + 1 and the transition from t + 1 to t follow the same law.
We can similarly express the idea of retrodictability:
| p(t + 1) = g[p( t)] → p(t) = h[ p(t + 1)] | [2] |
where h is a function derived from the recurrence formula, which allows ‘retrodiction’. The functions h and g may be totally different. For more precise definitions of reversibility and retrodictability, see Appendix 1.1 (continuous time) and 1.2 (discrete time).
Finally, there is another, important reason why retrodictability and reversibility should not be confused. So far, time-reversibility has been discussed only in the context of deterministic processes. However, time-reversibility can also be a property of stochastic processes: if the stochastic properties of a process depend on the direction of time, this process is said to be irreversible; if they are the same for either direction of time, the process is called reversible. Let X(t) be a stochastic process, and τ a time increment. A standard definition of time-reversibility for a stochastic process is:
“A stochastic process X(t) is reversible if (X(t1), X(t2), …, X(tn)) has the same distribution as (X(τ-t1), X(τ-t2), …, X(τ-tn)) for all t1, t2,…, tn”(Kelly 2011, p. 5) [3]
This definition means that the joint probabilities of the forward and reverse state sequences are the same for all sets of time increments. This notion can be applied to a Markovian process ( i.e. in a state of equilibrium), that is to say a random process that undergoes transition from one state to another with no memory of the past. In a state of equilibrium, the condition for reversibility is:
| ΠiPi,j = ΠjPj,i | [4] |
where Pi,j is the transition probability from state i to state j, and Πi Pi,j the probability flux from state i to state j. Πi is the proportion of the population in state i. This formula does not explicitly include the time parameter t, but time is implicit through the notion of transition.
This statistical notion of reversibility has been fruitfully applied to a number of subjects, such as queuing networks, migration processes, clustering processes (esp. the equilibrium distribution polymerization process), and also population genetics, where Markovian processes are tremendously important for the treatment of random genetic drift (Kelly 2011). In contrast with reversibility in deterministic systems, stochastic time-reversibility is hardly compatible with retrodictability. Retrodictability is ordinarily understood as the possibility to reconstitute the actual trajectory that led to the present state, and is strongly associated with determinism, or at least to the idea of a causal sequence that has driven the trajectory. The notion of retrodictability could perhaps be extended to stochastic processes, but this is not the usual way of thinking about it. Furthermore, this would probably be a strange way of thinking in the case of time-reversible stochastic evolution, because stochastic reversibility is a typical case of an invariant and stationary state.
To sum up, although simple in principle (insensitivity of a given law to time reversal), the ‘mathematical’ notion of reversibility is delicate. It is not synonymous with retrodictability, and it does not only apply in deterministic situations.
3.1.3 ‘Physical’ or ‘thermodynamic’ notion of reversibility
The ‘physical’ notion of reversibility is closely related to thermodynamics. Both denominations are unsatisfying, because the former arbitrarily restricts the notion of the ‘physical’[16] , while in fact the latter extends beyond thermodynamics. ‘Physical’ reversibility means that a physical system can spontaneously return to a prior physical state. A classical (although not perfect) example is given by a spring, which returns to its prior state after being elongated. By contrast, we do not expect that a broken glass will spontaneously find again its original shape. This is quite different from the property of insensitivity to time reversal. Consider a glass that breaks into pieces after falling. The glass would not be expected to spontaneously reacquire its original, ordered structure. Another example is that of a marble in a bowl. If there were absolutely no friction, the ball could go up and down the sides of the bowl indefinitely. But there is always some degree of friction. Therefore the oscillations of the marble will steadily decrease in amplitude, and in the absence of an external force, the marble will finally stop moving. These two examples (broken glass and rolling ball) illustrate the notion of physical irreversibility.
The traditional physical notion of reversibility is closely associated with thermodynamics: reversible evolution of a system is a type of evolution where no entropy is produced. Conversely, the greater the entropy, the more irreversible the transformation of the system. In a closed system, entropy is a quantity that can only increase. A precise definition of what this quantity precisely means is not needed here, nor are the classical debates on entropy as a property of macroscopic systems, as opposed to the reversible phenomena that underlie irreversible behaviour at a macroscopic level. For the needs of the present paper, suffice to retain that the physical (or thermodynamic) notions of reversibility and irreversibility are closely related to those of conservative vs. dissipative systems. A conservative system allows for reversible transformation; a dissipative system implies a dissipation of energy (e.g. diffusion of heat and friction), which renders the transformation irreversible, see chapter 5 for a short discussion on the origin of irreversibility in thermodynamics.
From a thermodynamic point of view, biological phenomena are widely thought to be far-from-equilibrium processes: they maintain a relatively low entropy thanks to flows of energy and matter. Because they produce entropy, they are irreversible from the thermodynamic perspective. However, this aspect concerns energy and energy dispersal in a space of positions and momenta (measured in physical units), which is different from the space of gene populations that we discuss in this paper (gene frequencies are not measured in physical units). As a result, thermodynamic irreversibility is analytically independent from the question of the intrinsic time-reversibility or time-irreversibility of population genetics models.
3.2 Retrodictability and reversibility in theoretical population genetics
The various notions of reversibility mentioned in the previous paragraph will now be applied to theoretical population biology. No attempt is made here to be exhaustive. The present analysis will be limited to a few typical cases. Stochastic and deterministic processes will be successively examined, and a few remarks will be made about cases of ‘reversibility’ in population genetics that do not fit with the proposed categorization, cases where the notion of evolutionary reversibility relies on specific biological processes.
3.2.1 Stochastic processes
Stochastic processes probably offer the best and most spectacular cases of time-reversibility in the strictest mathematical sense, that is to say insensitivity of a given model to reversal of time. This is most explicit in G. A. Watterson’s two articles on “Reversibility and the Age of an Allele” (1976 and 1977). These papers consider the probability distribution of the age of a mutant allele, whose present frequency is known. The ‘age of an allele’ is defined as the time that has elapsed between the introduction of the allele by mutation and the present. In the first paper (1976), the author assumes that there is no mutation and no selection. The model is set in discrete time, and admits that there is an infinite number of possible neutral alleles and thus discuss genetic drift. The method consists in taking y, the present frequency of the mutant gene, as “the initial state of a stochastic process, and studying how long diffusion would take to reach state x (or state 0) for the first time” (x being the frequency at a time t units prior to the present). Watterson is very explicit about the role of time-reversibility in his model, the general spirit of which is presented in the following terms:
“This interpretation seems surprising on two counts: first, because it means that the published results are simply moment of extinction times for diffusions, and second, there are stochastic processes for which this reversibility is valid, that is, processes whose behaviour looking into the past is statistically identical with their future behaviour.”(Watterson 1976, p. 240)
This declaration is accompanied by a no less explicit figure (Figure 1), illustrating the symmetry between the ‘age of an allele’ and ‘extinction time’.
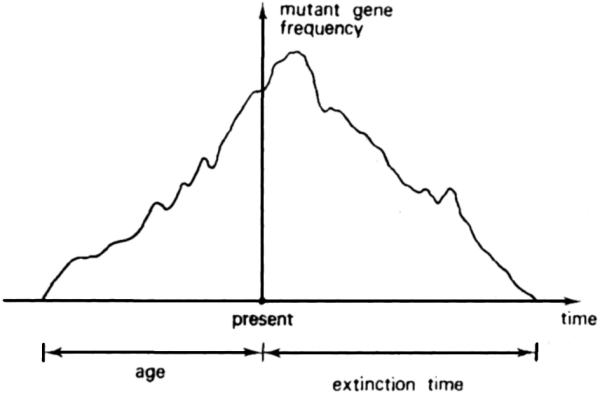
The model itself relies on an estimation of the probabilities of all the possible transitions from one state to another, in both directions of time (β→ β’ and β’→ β). Since the Markov chain considered has a stationary distribution, which means that the process described is time reversible (Kelly 2011), Watterson states:
“The consequence of reversibility for the stationary configuration process is that we can discuss its past evolution with equal ease as its future evolution; β(t), β( t-1), β(t-2), β(t-3),… have the same joint [sic. ‘probability’ ?] as have β(t), β(t+1), β(t+2), β(t+3),…ˮ(Watterson 1976, p. 243).
The main conclusion of the paper is that “…the age distribution {Pi( a)} for an allele now represented byi genes in the population is the same as the extinction time distribution for such an allele. Moreover, { Pi(a)} is independent of the frequencies of the other alleles in the population.” (Ibid., p. 246). This is a remarkable result, illustrating the usefulness of time-reversibility for the elaboration of models in population genetics: “By reversibility we mean that given the present state of a stochastic process, the statistical properties of its future behaviour are the same as those for its past history treated as a stochastic process with time running in the reverse direction.” (Watterson 1977, p. 179) Watterson’s notion of reversibility corresponds to that defined in equations [3] and [4].
In the same spirit, time-reversibility has been extensively used in coalescent theory, which is probably the major innovation in population genetics since the 1980s (Kingman 2000). Coalescent theory is concerned with gene genealogies within species. Relying on neutral mutations and the assumption of randomness of reproduction, its basic idea is to estimate the average time at which several genes share their most recent common ancestor. Time reversibility of the genealogical process is crucial in this case.
3.2.2 Deterministic processes
Population genetics theory is commonly divided into two main branches. The first is stochastic theory, which focuses on the effect of random changes, especially "random drift", in allelic and genotypic frequencies. The second focuses on “deterministic” effects of factors such as mutation, migration, selection, and mating system. The deterministic theory of population genetics ignores the random changes, and is therefore less complete than the stochastic theory (Ewens 2012). In fact, all real processes in nature include a stochastic aspect, not least because real populations are finite and inescapably subject to random drift. Consequently, in the real world, deterministic factors always interact with stochastic factors. Furthermore, when population geneticists speak of the evolutionary factors in terms of ‘forces’, it is only a metaphor. Some philosophers defend that population genetics does not deal with physical forces but with statistical effects (Walsh, Ariew, and Lewens 2002; Matthen and Ariew 2009; Huneman 2013). Nevertheless, the notion of ‘deterministic’ factors in population genetics is acceptable in the sense of factors that have a directional effect, and tend to push gene and genotypic frequencies in one direction, up, down, or intermediate. Recurrent mutation, selection, migration and non-random mating are the commonest cases of such deterministic factors. Just as forces in mechanics, they produce either secular changes that result most often in states of equilibrium such as the fixation of an allele at frequency 0 or 1 ( e.g. one-way mutation pressure), or maintenance of genetic frequencies at an intermediate value (e.g. two way recurrent mutation pressure, or selection with advantage to the heterozygote). The importance of these “deterministic factors” led J. B. S. Haldane to say that population genetics—especially the genetic theory of natural selection—is part of the “mechanics of evolution”. This is indeed a tempting metaphor, which one of the authors has endorsed in the past (Gayon 1998, Chap. 8). However, in view of the issue of the time-reversibility of equations, we are inclined to significant reservation about this metaphor. Thus, to what extent and in what sense are the equations describing the dynamics of deterministic processes in population genetics ‘reversible’?
3.2.2.1 Retrodictability
The issue of retrodictability will be considered first. Intuitively, if the existence of deterministic models in population genetics is accepted, the answer seems obvious. Richard Lewontin is particularly clear on this issue:
“It is usual for population geneticists, who claim that they are studying the dynamics of evolution, to divide the kinds of models that they deal with in two sorts. They talk about deterministic models and about stochastic models? What is meant by deterministic models is that, given the initial conditions of the population, which I will simply specify by X0 (although that will be some sort of a vector of conditions of the population), and some set of parameters, then it is possible to predict exactly the condition of the population at some other time, τ.”(Lewontin 1967, p. 81)
By “some other time”, Lewontin means any other time, past or future, as explicited a few pages later in the famous 1967 paper on “historicity in evolution”: “If I just give you one history of a deterministic population because it is deterministic I can say everything about its past” (Lewontin 1967, p. 87). This is exactly what retrodictability means.
Population genetics textbooks are replete with deterministic models describing the effects on gene and/or genotypic frequencies, of factors such as recurrent mutation, migration, selection, and mating system. In these models, evolutionary time can be treated in two ways, discrete or continuous[17] . With discrete time, the time-unit is a generation, and the evolutionary dynamics of the population is described by recurrence equations. Continuous time means that generations overlap and that continuous change is assumed (with no discrete time intervals whatever). In fact, the typology of models with respect to time is a bit more complicated (See Crow and Kimura 1970, Chapter 1, “Models of Population Growth”, 1.1 to 1.4), but this will not be enlarged upon here. The type of model chosen will depend on the organisms being considered. For instance, models with discrete and non-overlapping generations are realistic with annual plants; models with overlapping generations with discrete time intervals are appropriate for animals or plants with a specific breeding season but which survive for several successive seasons. In other cases, birth and deaths occur at all times, and the most realistic models are based on the assumption of overlapping generations and continuous change. Thus, the basic method relies on differential equations. Ronald Fisher favoured this method, which is typically appropriate for the human species. Nonetheless, models relying on discrete time and recurrence equations quite often offer an acceptable first approximation, and are then preferred because of their mathematical simplicity.
Retrodictability seems to be a general property of deterministic models in population genetics. There may be special cases, where retrodiction is rendered impossible because of mathematical intractability. In other cases, recurrence equations may not be inverted because a state has several preceding states, generating ambiguity in the retrodiction (see Appendix 1); these will not be discussed here. Consider now two examples of retrodictability.
First the case of a population subjected to a recurrent one-way mutation. Since mutation rates are usually very small (10-5 to 10-9), the time taken to reduce p from a value close to 1 to a value close to 0 is extremely long. For instance, if the mutation rate is 10-6, and if the initial frequency p is 0.9, it will take 2.2 million generations to reduce the frequency of p to 0.1[18] . Therefore, mutation pressure alone is not likely to be a major cause of evolution, because other factors, particularly random drift and selection, will very probably supersede the effect of recurrent mutation. Nevertheless, if isolated from any other consideration, it can be precisely described. The effect of recurrent mutation on the frequency of the mutated gene is:
| p(t+1) = (1–u) p(t) | [5] |
where u is the probability that a ‘normal’ allele A of frequency p mutates to a.
Since (1-u) is the probability that A does not mutate, [5] says that p at time t+1 is the fraction of A alleles that do not mutate (Roughgarden 1979, p. 43-45). Equation [5] can be iterated analytically:
| p(1) = (1–u) p(0) p(2) = (1–u) p(1) = (1–u)2 p(0) p(3) = (1–u) p(2) = (1–u)3 p(0), etc. |
Whence the generalization:
| p(t)= (1–u)t p(0) | [6] |
Each generation raises (1-u) to the new high power. Since (1-u) is <1, the frequency of a gene reduces at a rate that itself decreases, because the quantity of alleles A in the population is reduced at each generation. This deterministic process is represented in figure 2 for p(0)= 0.9, and various values for the mutation pressure u. It is easy to see why this ‘law’ makes retrodiction possible. At any generation t, the frequency at previous generation t-1 can be obtained by dividing p(t) = (1-u)t p(0) by the quantity (1-u). Figure 2 illustrates the evolution of the frequency of the mutated gene for p(0) = 0.9 and various values of u. The very possibility of drawing such a curve strongly suggests that the phenomenon is both predictable and retrodictable.

A similar operation can be done for selection at a diallelic locus with constant selective values W11, W12, W22, one of the simplest cases of selection. In the case of discrete generations, all textbooks give the same basic recurrence equation for this process[19] (p: frequency of allele A; q: frequency of allele a; p+q = 1):
p(t+1) = (p(t)W11 + q(t)W12) p(t) / (p(t)2W11 + 2 p(t) q(t)W12 + p2W22) [7]
The expression (p(t)W11 + q(t)W12) in the numerator is the selective value WA of allele A (average selective value of all genotypes including allele A). The denominator is the mean selective value of population W (mean of the selective values of the different genotypes weighted by the frequencies of these genotypes). Equation [7] can thus be written:
| p(t+1) = p(t) WA / W |
In fact this formula applies to all alleles. Therefore, if pi is the frequency of allele i, and pi’ the frequency of i in the next generation:
| pi’ = piWi / W | [8] |
This is a non-linear equation. Except in very special cases, there is no general method to iterate it analytically, but this can be done manually or using a computer—an easy operation for anyone today with an application like Populus[20] . Figure 6 (Appendix 3) gives the result of computer iterations from [7] for selection against a recessive allele with strong selection. This is an illustration of a typically deterministic process.
Although analytical iteration is not accessible, it is possible to iterate backwards generation-by-generation. Appendix 2.2 provides a demonstration of the possibility of retrodiction in the case of a model of selection at a diallelic locus with W11 > W12> W22. This result could reasonably be extended to all possible fitness ratios, because the backward equation is quadratic and its coefficients show that it has only one positive solution (Anthony Edwards, personal communication). Therefore, at least in this case, retrodiction is possible. Note that the backward equation is derived from the forward equation. Appendix 2.2 also shows why reversibility is not satisfied for the same model. This brings us to the issue of time-reversibility in population genetics.
3.2.2.2 Time-reversibility (mathematical sense)
The question of whether the deterministic models of population genetics are reversible in the usual mathematical sense is the most delicate problem. If yes, the ‘laws’ expressed by them should be unaffected by time reversal, that is substituting -t for t in the equations (see section 3.1.2). Since the notion of ‘law’ is important here, it is worth recalling Elliott Sober’s proposal. According to him, the traditional logical empiricist concept of law requires that laws be statements that are both truly universal (that is to say not referring to any place, time, or individual) and empirical. This concept is inappropriate for various domains of science, especially evolution, where the second condition (being an empirical statement) is questionable. For Sober (1997), the process of evolution as studied in population genetics “is governed by models that can be known to be a priori true”. These models are mathematical truths, which describe how systems of specified type develop through time, whence Sober’s expression “process law”. For instance, given Mendel’s laws, and an operational definition of notions such as recurrent mutation, selective value, etc., the process laws of population genetics describe how these factors determine the trajectory of a population in the space of gene frequencies. This viewpoint is endorsed here (Sober 1984, 1997; see also Brandon 1997, and Gayon 2014).
The reason why the notion of law is important here is that time-reversibility is not so much a property of a trajectory as a property of the law that governs the dynamics of the system, and therefore underlies the trajectory. Strictly speaking, the property of time-reversibility tells us nothing about the capacity of a given system to ‘return’ to its former state. This is not excluded, but will depend on the actual conditions imposed on the system. Time-reversibility is a property of a law of transformation that applies to transformations in both directions, whatever the actual fate of the system. For instance, the reversibility of Newton’s law (F = ma) does not mean that a given body submitted to force F could effectively come back to a prior state, but that, if it did, the law would still apply. Thus, mathematical reversibility evokes counter-factual prediction, not the capacity of a given system to spontaneously return to a prior state (thermodynamic reversibility, see below). Of course, the two notions are often closely related in actual scientific practice, just as retrodictability and mathematical time-reversibility are often connected. However, the concepts are distinct.
Returning now to the examples of recurrent mutation and selection, using exactly the same models as in the previous paragraphs leads to the question “Are the ‘laws’ expressed in the recurrence equations time-reversible?”
Case 1: Recurrent mutation
The position defended here is that the recurrence equation describing this process is not time reversible. This thesis goes against a common intuition. Since it is one of the simplest dynamic models in population genetics, it will be treated in detail[21] .
To begin with, let us formally define the concept of time reversibility in a dynamic system, the evolution of which can be described by a recurrence equation. We assume that the state of a system x(t) at time t is a function of the p previous states:
| x(t) = f ( x(t-1), x( t-2),…, x( t-p)) | [9] |
Given that [9] is time-reversible for any sequence (x(0), x(1),…, x(T)) solution of [9], so the reverse sequence ( x(T), x(T-1),…, x(0)) is also a solution of [9].
Before applying this definition to the one-way recurrent mutation model, an example of a recurrence equation that satisfies our definition of time-reversibility will first be given.
Consider the following recurrence equation:
| x(t+2) = 2 x( t+1) – x(t) + 1 | [10] |
It can easily be checked that the sequence (0, 1, 3, 6, 10, 15) is a solution of [10].
| x(0) = 0 (initial condition) x(1) = 1 (initial condition) x(2) = (2 x 1) – 0 + 1 = 3 x(3) = (2 x 3) – 1 + 1 = 6 x(4) = (2 x 6) – 3 + 1 = 10 x(5) = (2 x 10) – 6 + 1 = 15 |
Surprisingly, the reverse sequence (15, 10, 6, 3, 1, 0) is also a solution of [10]:
| x(0) = 15 (initial condition) x(1) = 10 (initial condition) x(2) = (2 x 10) – 15 + 1 = 6 x(3) = (2 x 6) – 10 + 1 = 3 x(4) = (2 x 3) – 6 + 1 = 1 x(5) = (2 x 1) – 3 + 1 = 0 |
More generally, for any sequence (x(0), x(1),…, x(T)) solution of [10], it is possible to prove that the reverse sequence (x(T), x( T-1),…, x(0)) is also a solution of [10]. Therefore [10] is time-reversible.
Consider now the recurrence equation describing the evolution of the frequency p of an allele A subject to recurrent mutation. As seen above [5], this equation is:
| p(t+1) = (1–u) p(t) |
The sequence (1, (1-u), (1-u)2) is solution of [5] :
| p(0) = 1 (initial condition) p(1) = (1-u) x 1 = (1-u) p(2) = (1-u) x (1-u) = (1-u)2 |
On the other hand, the reverse sequence ((1-u)2, (1-u), 1) is obviously not a solution of [5] when u ≠ 0. If the initial condition is (1-u)2, then the sequence obtained by applying [5] is
| p(0) = (1-u)2 (initial condition) p(1) = (1-u) x (1-u)2 = (1- u)3 p(2) = (1-u) x (1-u)3 = (1- u)4 |
We conclude that equation [5] describing the evolution of a population under recurrent mutation pressure is not time-reversible when u≠0 (in the case u=0, the population never changes which is time reversible).
More generally, if any solution of [9] is strictly decreasing (respectively increasing), then [9] is not time reversible.
However, we anticipate an objection. The practicing population geneticist might say that reversing the direction of mutation (a→A instead of A→a) would amount to ‘reversing the process’. To make things as symmetrical as possible, a rate of reverse mutation equal to the rate of direct mutation could be taken, and begin with a frequency of say 0.9 in both directions. A law of the same general form would describe the ‘reverse’ dynamics and trajectory, with v (mutation rate for a→A) replacing u (mutation rate for A→a). But this would be another process; because a crucial parameter, with a different biological meaning (reverse mutation) has been introduced, it is not the same law. Changing the direction of mutation does not amount to changing the direction of time. ‘Reverse mutation’ is a biological concept, which should not be confused with the question of whether the process law describing the diffusion of a ‘recurrent’ mutation is ‘reversible’ or not.
Case 2: Basic models of selection
The basic equation to predict the evolution of gene frequencies for a diallelic selection submitted to selection has been given in [7]. This recurrence equation is a rather general one. It ignores the various possible relations between the selective values, for instance: selection against a recessive gene (W22< W12 =W11), selection against the dominant allele ( W11 < W22 = W12), incomplete dominance (W11< W12< W22 or W22< W12< W11), or advantage to the heterozygote (W12 superior to the two other genotypic selective values). In all cases, selective values are assumed to be constant.
Now, given [8],
| | [11] |
with: pi: frequency of allele Ai; Wi : average selective value (or “fitness”) of the Ai allele (= average selective value of all genotypes containing Ai ); W: average fitness of the population (average fitness of all genes at this locus, or average fitness of all the genotypes at the same locus in the population).
Equation [11] is of fundamental importance for the genetical theory of natural selection. As underlined by Crow and Kimura (1990, p. 180), it shows that the rate of change of gene frequency is proportional to: (1) the gene frequencies, pi (1-pi), which means that a very rare or very common gene will change slowly, regardless of how strongly it is selected; (2) the average excess in fitness of the Ai allele over the population average ( Wi – W), which can be either positive or negative. If Wi – W is positive, the frequency of the allele will increase; if negative, it will decrease. Whether
Before commenting on reversibility, another crucial notion must be introduced. If the selective values are kept constant, Δpi can be rewritten as:
| | [12] |
This famous equation is known as “Wright’s formula” (Wright 1937, 1940). It is fundamental because it connects the change in gene frequency Δp, with the slope of the function W (average fitness). It shows that if W is at a maximum with respect to p, then Δp is zero, or in other words the population is at equilibrium. W is classically interpreted as the “fitness function” or the “adaptive topography”. Since W maximizes, a population submitted to selection is seen as “going uphill”. Figures 3, 4, 5, 6, 7, (Appendix 3) borrowed from Albert Jacquard (1971), give a clear graphic expression of the connection between Δp and W in various cases; these are actually the most common situations taught in an elementary course of population genetics. On these graphs, W11, W12, W22 are the selective values (or ‘fitnesses’). By convention, Jacquard has systematically taken W11 ≤ W22, and p is the frequency of the unfavoured gene (numbered “1”). This is why Δp is most often negative. (It would be equivalent to observe the increase of the favoured gene; Δ p would then be positive; but of course the order of alleles on the graph should be inverted). The arrows in the figures show that W is always ≥ 0 and is systematically maximized. Equilibrium is attained when W is maximal; this maximal value of W corresponds to Δ p = 0. In Figures 3, 4, 5, the equilibrium is realized when p = 0 (the unfavoured gene disappears, the other gets fixed). In Figure 6 (heterozygote inferiority), there are two stable equilibriums, p = 0 and p = 1, the outcome depending on the initial conditions). In Figure 7 (heterozygote superiority), the population stabilizes for an intermediate value of p: selection maintains variation. Figures 8 and 9 are examples of the trajectories of populations submitted to two kinds of selective pressure abundantly realized in nature: selection against a recessive allele (Figure 8), and selection with heterozygote superiority (Figure 9). In each case, several curves are given, corresponding to selective pressures of varying intensity. The trajectory given in Figure 8 corresponds to the dynamics represented in Figure 5 (selection against a recessive). The trajectory given in Figure 9 corresponds to the dynamics represented in Figure 7 (heterozygote superiority). The trajectories represented in Figures 8 and 9 are the result of computer iterations from the basic recurrence equation. As observed by Roughgarden (1979), it is remarkable that equation [12] despite its important restrictive condition (constancy of selective values), can generate so many different trajectories.
Are these models time-reversible? Formally, it would be useful here to provide a detailed proof that the basic recurrence equation [7], or its special applications (sometimes with simplifying assumption) to particular cases ( e.g. Crow and Kimura 1970, equations 5.2.2, and 5.2.14 to 5.2.17), or the treatment of the same problems with continuous time (e.g. Crow and Kimura 1970, eq. 5.2.8 to 5.2.11) are not time-reversible. This will be treated in a future publication. For the time being, Appendix 2.2 provides a proof in the special case of a diallelic model with W11 > W12 > W22. It shows that the dynamics of this system are retrodictable but not reversible. In fact the situation is identical to that of recurrent mutation. In both cases, it is possible to derive a rule for retrodiction, but this rule is obviously incompatible with the idea that the dynamic equation is reversible.
Furthermore, it should be observed that all standard models of selection with constant selective values describe dynamics that are driven by a maximizing function (maximization W of the average selective value of the population). Therefore it seems hard to imagine that such models could be used to describe a reverse transformation obeying exactly the same law: what would it mean for a population to accomplish the reverse trajectory with W minimized throughout? This would contradict the models. To sum up, all elementary models of selection evoked in the present chapter are deterministic and retrodictable, but they do not seem to describe a time-reversible process.
One final observation on this subject. We mentioned earlier that in selective models with constant genotypic selective values, the average selective value always increases from generation to generation, until it becomes equal to zero when equilibrium is attained, therefore ΔW ≥ 0. However, should this be understood strictly or approximately? Is there room for oscillation, as was often suggested in elementary courses of population genetics some decades ago, especially in the case of heterozygote superiority (see Figure 7)? The idea was that the population rises through the adaptive topography a little like a ball which runs down a bowl, goes up the other side of the bowl, comes back, runs up again, etc. However, it has been demonstrated that there is no room for oscillation (Roughgarden 1979). This comes as no surprise if selection takes a population close to the fixation of one of the alleles: once the gene is fixed, no variation is left, and therefore there is no room for further selection. But in the case of heterozygote advantage, this is somewhat more surprising. Roughgarden (1979, p. 51-53) notes that there is no possibility of “overshoots that are so large as to prevent the convergence to
3.2.2.3 ‘Physical’ or ‘thermodynamic’ reversibility
Physical reversibility is the possibility for a system to return spontaneously to a previous state. Does this apply to population genetics? This subject will not be treated here in detail. A few glimpses will suffice. Since Ronald Fisher, the directionality of evolution under natural selection has been regularly compared with the directionality implied by the Second Law of Thermodynamics. The Second Law asserts that irreversible physical processes imply a unidirectional increase of entropy. In his Genetical Theory of Natural Selection (1930), Fisher ‘immediately recognized certain formal analogies between the mechanistic models introduced by Boltzmann (1896) to analyse physical systems, and the selection models proposed by Darwin (1859) to explain adaptation in biological systems’ (Demetrius 2000). According to Demetrius, Fisher’s fundamental theorem of natural selection is indeed a directionality theorem. This theorem states that ‘The rate of increase of fitness of any species is equal to the genetic variance in fitness’ (Fisher 1930, p. 50). By this formula, Fisher meant that the speed of action of selection is a function of the additive genetic variance[23] .
It is worth quoting Fisher here who compares his fundamental theorem with the Second Law of Thermodynamics:
“Both are properties of populations, or aggregates, true irrespective of the nature of the units which compose them; both are statistical laws ; each requires the constant increase of a measurable quantity, in the one case the entropy of a physical system and in the other the fitness, measured by m, of a biological population. As in the physical world we can conceive of theoretical systems in which dissipative forces are wholly absent, and in which the entropy consequently remains constant, so we can conceive, though we need not expect to find, biological populations in which the genetic variance is absolutely zero, and in which fitness does not increase.”(Fisher [1930] 1958, p. 39)
In spite of these resemblances[24] , Fisher’s objective was in fact to emphasize the differences between the Second Law of Thermodynamics and his theorem. Among the five differences that he mentions, one is of special interest for our subject: “Entropy changes are exceptional in the physical word in being irreversible, while irreversible evolutionary changes form no exception among biological phenomena” (Fisher, ibid., p. 40).
In fact, modern population biologists, or at least some of them, compare entropy and fitness more literally than Fisher used to. A stimulating example is Lloyd Demetrius, who proposes an adaptation of the concept of entropy to evolutionary genetics and ecology, and puts forward the concept of “evolutionary entropy”: a measure of the dispersion of the age of the ancestors of a randomly chosen newborn. Demetrius’ concept of evolutionary entropy is an explicit attempt to overcome the obvious difference between statistical thermodynamics and population biology; thermodynamics deals with the properties of populations of inert particles, whereas population biology treats the properties of populations of living objects which reproduce, and therefore grow. To overcome this difficulty, Demetrius points to a “formal correspondence” between the thermodynamic variables and the population parameters intervening in population biology: “growth rate” corresponds to free energy; “generation time” corresponds to inverse temperature; “evolutionary entropy” corresponds to thermodynamic entropy. Then, both situations follow the same equations with the appropriate variables (Demetrius 2000). Demetrius’ basic intention is to offer an alternative to Fisher’s conception of directional change in mean fitness: Fisher’s fundamental theorem is based on the relative viability of individuals within the population; Demetrius takes into account the absolute survival and reproduction of populations. In Demetrius’ terms, “Darwinian fitness is completely described by evolutionary entropy, a demographic variable which measures the heterogeneity in the age of reproducing individuals in the population.” (Demetrius 2000, p. 2) Moreover, “[evolutionary] entropy characterizes Darwinian fitness, the efficiency with which a population acquires and converts resources into viable offspring. Accordingly, entropy predicts the outcome of natural selection in populations subject to different classes of ecological constraints.” (Demetrius, Legendre, and Harremoës 2009) We acknowledge that we feel rather uncertain about the precise sense in which “evolutionary entropy” and entropy in the ordinary physical sense are correlated. As Demetrius & al. recognize, evolutionary entropy is “analogue of the Gibbs–Boltzmann entropy in statistical thermodynamics”. This analogy is grounded both in a formal similarity of equations, and in the distinction between a microscopic[25] and a macroscopic description[26] . Suffice to say that Demetrius’s stimulating proposal represents just one way among others to bridge the gap between population genetics and population ecology, with its emphasis on absolute fitness, population density, and bounded vs. unbounded population growth[27] .
Demetrius’ proposal will not be analysed further here. What matters for the present paper is a consequence of his approach to the question of whether the evolutionary dynamics are reversible or not in a thermodynamic (or thermodynamic-like) sense. Rather than emphasizing the kind of unlimited evolutionary irreversibility that Fisher favoured, Demetrius offers a tool that leaves room for both evolutionary irreversible processes (characterized by unidirectional increase of evolutionary entropy), and evolutionary reversible (or virtually stationary) processes. In such a theoretical framework, the reversible/non reversible distinction is not an all or nothing alternative, but rather a tool for describing the dynamics of evolutionary change (Demetrius 2000. For a comprehensive description of this field of research, see Weber, Depew and Smith 1988).
This area of research is fascinating and innovative, but remains quite speculative today. Are there real analogies with friction and heat dissipation in the models of population genetics and ecology, or are these comparisons no more than suggestive metaphors or mathematical analogies? This question will be left open (For a survey of this field of research, see Weber, Depew and Smith 1988).
3.2.2.4 Other senses of reversibility in population genetics
The intuitive notion of reversibility (see above, 2.1, introduction) sometimes encountered among population geneticists will now be reconsidered. For a population geneticist, who usually works at a small evolutionary temporal scale, it seems obvious that most often a given population can return to a prior state. For instance, if a recurrent mutation spreads on its own and is fixed, in principle a reverse recurrent mutation can do the same. If natural selection causes the expansion of an allele in the population, it is always possible that selective pressure in the other direction returns the population to its initial state. If random drift leads to the fixation of a mutated allele, a reverse mutation followed by drift or selection may cause ‘reverse’ evolution. And so on.
There is no doubt about the plausibility and effectiveness of such processes. But they mean something different from the various senses of reversibility analysed above. Recurrent reverse mutation has been discussed, consider now the case of selection. In the haploid case, how far would an inversion of the selection coefficient amount to a ‘reversible process’ in a technical sense close to time-reversibility? Appendix 2.1 provides a formal treatment of this problem in the simple case of haploid populations. The method consists in replacing the selective values Wi (haploid populations) with the inverse quantities 1/ Wi in the recurrence equation. This inversion preserves the relative values of the Ws, but in reverse order. The question then, is whether the inversion of the fitness values preserves the ‘law’ expressed in the recurrence equation or not. The calculation shows that the dynamics of the initial equation is preserved with the new parameters 1/Wi. Therefore, the ‘law’ is preserved by time reversal, except for the constants. This is not ‘time-reversibility’ in the strict sense, but could be named weaker time reversibility (for a definition, see Appendix, 1., 1.2, and example in 2.1). Incidentally, this demonstration applies to as many alleles and corresponding selective values as required.
Would the same methodology produce a similar case in the case of selection on sexually reproducing diploid population? Certainly not. Suppose for instance that the heterozygote is advantaged, ie. W12 greater than both W11 and W22. The dynamics of such selection is represented in Figure 7. If the values of the Wij were inverted, i.e. if the Wij were replaced by expressions of the form 1/ Wij, then we would have W12 smaller than both W11 and W22. This would correspond to the dynamics represented in Figure 6 (underdominance), with an unstable equilibrium, and two possible equilibria ( p = 0 and p = 1). This is indeed a totally different dynamics. The same could be said of other possible ratios for the Ws, except when
3.3 Conclusions on reversibility in theoretical population biology
Although the analysis above remains somewhat sketchy and incomplete, the conclusions that it suggests are quite straightforward:
- Reversibility in the sense of retrodictability (in fact an improper use of the word) seems obvious for deterministic models, with possible exceptions in discrete time. It does not apply to stochastic models.
- Time-reversibility is clearly instantiated in some important stochastic models; it seems inadequate for deterministic models. In one case (selection in a haploid population), one comes close to time-reversibility since a weaker definition than the usual one is met. However, this subject would require more extensive and detailed examination.
- Thermodynamic reversibility, which is a fascinating subject, remains mainly a matter of speculation.
- In classical models of selection, the average selective W can hardly be interpreted as a potential function (see n. 11).
4. Conclusions
Two broad conclusions can be drawn. The first conclusion bears on lawfulness in evolutionary biology. Laws do not need to be empirically true statements of unlimited universal scope; they can also be “models that can be known to be true a priori” (Sober 1997). Not all mathematical truths are laws, only those that elaborate on the basis of some empirically plausible conditions. For instance, if Mendelian inheritance is assumed, and if such factors as mutation, migration, mating system and selection are plausible evolutionary factors, then it is possible to derive the typical behaviour of a population under specified conditions. The abstract descriptions obtained are idealizations, no more and no less than those developed by the physical sciences. The question of whether they are useful to predict the actual behaviour of populations or not is irrelevant to their nomological status. They just say that, if conditions C1, C2,…, Cn are met, then a specific behaviour should be observed. The Hardy and Weinberg equilibrium is a good example: provided that the six conditions stated in 2.2 are satisfied, then the genetic structure of a population is constant over time. Of course no biologist believes that actual populations are infinite, but the model opens the possibility of making other models that will explain the deviations as a function of population size. Therefore the problem is not whether the HW equilibrium is strictly true from an empirical point of view, but how useful it is for explaining and predicting the behaviour of real populations, in combination with other models that will take into account the fact that this or that condition is not met, and to which degree it is not met. Nevertheless, the HW law remains a mathematical truth if the standard conditions are met. Some philosophers might argue here that it would be wiser to give up the term ‘law’ and just speak of ‘models’. This is maybe the case. In practice, population geneticists use the terms ‘law’ and ‘model’ indifferently to qualify the HW equilibrium. In other cases (e.g. treatment of the effects of mutation, selection or population size), they tend to prefer ‘model’. We do not think that this is a crucial issue. Whatever the outcome of such a discussion, one important conclusion of this chapter is that an impressive number of results of theoretical population genetics consist in equilibria, which qualifies population genetics as a genuine science able to identify properties of invariance through transformation. The discovery of such properties has been a distinctive feature of modern science since its inception.
In population genetics, invariance to transformation is mainly defined with reference to the genetic structure of a population. Under a number of conditions, this structure may stabilize. One of the most characteristic features of population genetics as a field of research is indeed the search for “trends towards equilibria”. When browsing through text-books, it is amazing to observe in population genetics the definition of the equilibrium, and the estimation of the time required to come close to it, is declared to be more important than the precise description of the trajectory. This is what Haldane meant when he stated that a good deal of evolutionary theory deals with the ‘statics’ rather than the ‘dynamics’ of evolution (Haldane 1954).
The second conclusion of this enquiry comes to temper the first one. Time-reversibility has also been said to be a major characteristic of modern science, with special reference to classical mechanics. In the theory of population genetics, time-reversibility is obviously and abundantly present in the treatment of stochastic evolutionary processes. But this is a rather particular sense of reversibility (symmetry of probability distributions in both directions of time). As far as the authors have been able to judge from this first exploratory enquiry, time-reversibility in its mathematical sense does not seem to be a property of the models describing deterministic phenomena. But this problem will have to be examined in a more systematic way. Deterministic models in population genetics are highly retrodictable but this property is not identical to time-reversibility.
Time reversibility is a very impressive property of the equations of classical mechanics in the case of fundamental forces. In classical mechanics, objects follow the principle of inertia so that a homogeneous rectilinear movement does not require an external cause. The structure of selection models in population genetics is different. The changes in a population are directly driven by differences in fitness. If these differences cease to be, then the changes in the population stop immediately. In this sense, selection in population genetics is closer to a mathematized Aristotelian mechanics than to classical mechanics. In classical mechanics energy is conserved and is transferred from potential energy to kinetic energy and vice versa, which ensures the time reversibility of the dynamics. In population genetics, Wright’s equation describes a gradient ascent akin to classical potentials, but there is no equivalent to the kinetic energy that would enable the system to descend the gradient, which would be required for time reversibility.
To end up, the present publication is the first part of a broader enquiry on repetition and reversibility in evolution, both at the theoretical and the experimental level. A further paper will examine the rather different problems raised by the issues of the repeatability of experiments in experimental population biology, and of the capacity of populations or species to return to a prior evolutionary state.
Acknowledgements
Maël Montévil’s work is supported by a grant from the labex “Who am I?”. This paper has benefited from extensive discussion and collaboration with Jean-Philippe Gayon, who has been enormously helpful in clarifying the notion of time reversibility from a mathematical point of view. We also thank Anthony Edwards, Pierre-Henri Gouyon, and Michel Veuille. Their great competence in population genetics has been very fruitful to our understanding of the issue of reversibility in population genetics models. We also thank Edwards and Veuille or their careful reading of the text. We thank Elliott Sober for his careful reading of the paper and for his fruitful comments. Véronique Charrière is warmly thanked for her careful linguistic corrections and suggestions.
Appendices
Appendix 1 provides a formal definition of symmetry by time reversal and of retrodictability. Appendix 2 applies these definitions to some population genetics models. Appendix 3 contains the figures 3, 4, 5, 6 and 7.
1. Time reversibility
As discussed in the body of the text, time reversibility corresponds intuitively to a situation where the dynamics follow the same law before and after time reversal. Only deterministic dynamics are considered here.
1.1 Continuous time
In continuous time, a dynamic is typically defined by differential equations. A fairly general definition of differential equations is admitted here:
| | (1) |
where the
Mathematical notion of time reversibility
Time reversal means substituting –t to t in an equation. Time reversibility describes situations where the equation
| | (2) |
Weaker time reversibility
We propose a weaker notion of time reversibility, where F is preserved even though the parameters
| | (3) |
A supplementary condition is required for this notion to have a theoretical meaning. The
Retrodictability
The Cauchy-Lipschitz theorem also called Picard–Lindelöf theorem, states that under very general hypotheses on the regularity of
As mentioned in the main text, the issue of dynamics sensitive to initial conditions, such as the three-body problem in mechanics have not been discussed here. Let us just mention that in these cases, the impossibility of a perfect measurement of the initial conditions prevents empirical long term predictions and retrodictions because small differences have significant consequences.
1.2 Discrete time
Dynamics defined by recurrence will now be discussed:
Mathematical notion of time reversibility
The transitions
Weak time reversibility
By analogy with the continuous case, changes in the values of the parameters of
Note also that the new parameters must have a physical or biological meaning.
Example:
Retrodictability
Retrodictability corresponds to the fact that the reverse dynamic is deterministic. A system is retrodictable when a function h exists that satisfies:
Function
Example:
Counter example:
2. Application to models of population genetics
In this part, the reversibility of two classical models of selection in population genetics are discussed. In one case (asexual haploid population), the dynamic is reversible in the weak sense. In the second case (diploid, diallelic locus), the dynamic is retrodictable but not reversible.
2.1 Asexual haploid population: a weakly reversible model
We start with a classical model of selection at a single locus in a haploid population.
| | (4) |
To assess the properties of this dynamic with respect to time reversal, let us write
| | (5) |
Equation (5) can also be written:
| | (6) |
Here
By definition, we have :
| | (7) |
It is also possible to do this computation on the basis of the analytical expression of
| | (8) |
This equation has exactly the same form as equation (4). Therefore the dynamic is weakly reversible.
2.2 Sexual diploid population: a retrodictable but irreversible model
A population with two alleles at a single locus is now considered. The relative fitnesses are
| | (9) |
We use
This leads to a quadratic equation, where
| | |
| | (10) |
The reduced discriminant determines the solutions of such an equation. If the discriminant is positive, there are two mathematical solutions and no solutions if it is negative.
| | (11) |
If
| | (12) |
Because
| | (13) |
| | (14) |
Consider now time reversal. Equation (9) gives
Interestingly, the case where the square root disappears,
3. Figures 3, 4, 5, 6 and 7
 | 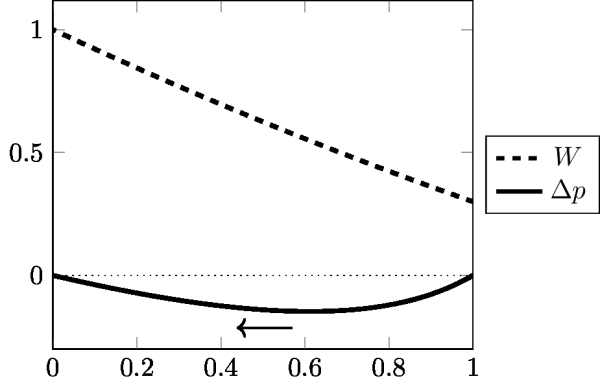 |
 |  |
 |  |
 |  |
 |  |


References
- Beatty, J. 1995. The evolutionary contingency thesis. Concepts, theories, and rationality in the biological sciences: 45-81.
- Boltzmann, L. 1896. Vorlesungen über Gas Theorie. Leipzig, Germany: Barth.
- Brandon, R. 1997. Does biology have laws ? The experimental evidence. Philosophy of Science, 64, Supplement. Biennial Meetings of the Philosophy of Science Association. Part II: Symposia Papers (Dec., 1997), S444-S457.
- Crow, J. & Kimura, M. 1970. An Introduction to Population genetics Theory. New York, Evanston, and London: Harper & Row, Publishers.
- Darwin, C. 1859. On the origin of species. London: Murray.
- Demetrius, L. 1992. Growth rate, population entropy and evolutionary dynamics, Theoretical Population Biology, 41: 208-223.
- Demetrius, L. 2000. Thermodynamics and Evolution. Journal of theoretical Biology, 206: 1-16.
- Demetrius, L., Legendre, S. and Harremöes, P., 2009. Evolutionary entropy: a predictor of body size, metabolic rate and maximal life span. Bulletin of mathematical biology, 71(4): 800-818.
- Dollo, L., 1893. Les lois de l’évolution. Bulletin de la Société Belge de géologie, paleontology, et hydrologie, 7: 164-166. [English translation in Gould 1970, p. 210-212].
- Edwards, A. W. F. 1977. Foundationsof Mathematical Genetics. Cambridge (UK): Cambridge University Press.
- Edwards, A. W. F. 2000. Sewall Wright’s equation
- Ewens, W. 2012. James F. Crow and the Stochastic Theory of Population Genetics. Genetics, 190, 2: 287-290.
- Fisher, R. A. 1918. The correlation between relatives on the supposition of Mendelian inheritance. Transactions of the Royal Society of Edinburgh, 52: 399-433.
- Fisher, R. [1930] 1958. The Genetical Theory of Natural Selection. Oxford: Clarendon, 2nd edn 1958. New York: Dover.
- Fisher, R. A. 1941. Average excess and average effect of a gene substitution. Annals of Eugenics,11: 53-63.
- Gayon, J. 1998. Darwinism's Struggle for Survival : Heredity and the Hypothesis of Natural Selection, Cambridge University Press, 1998.
- Gayon, J. 2014. De la portée des théories biologiques. In: T. Martin, ed., Problèmes théoriques et pratiques en biologie évolutionnaire, Besançon, Presses Universitaires de Franche Comté, p. 13-52
- Gould, S. J. 1970. Dollo on Dollo’s Law: Irreversibility and the Status of Evolutionary Laws. Journal of the history of biology, 3, 2: 189-212.
- Goux, J. M. 1979. Les modèles en génétique des populations. In: P. Delattre & M. Thellier, eds., Élaboration et justification des modèles: applications en biologie, Vol. II. Paris: Maloine, pp. 565-571.
- Griffiths, Paul E. 1996. The Historical Turn in the Study of Adaptation. The British Journal for the Philosophy of Science, 47, 4: 511-532.
- Haldane, J. B. S. 1954. The Statics of Evolution. In: J. S. Huxley, A. C. Hardy, and E. B. Ford (eds.). Evolution as a Process. London: Allen and Unwin, p. 109-121.
- Hardy, G. H. 1908. Mendelian proportions in a mixed population. Science, 28: 49-50.
- Hartl D. L. 1980 Principles of Population Genetics. Sunderland (MA, Sinauer Associates.
- Huneman, P. 2013. Assessing Statistical Views of Natural Selection: Is There a Room for Non Local Causation?” Studies in History and Philosophy of Biological and Biomedical Sciences 44: 604–612
- Jacquard, A. 1971. Structures génétiques des populations. Paris, Masson. Engl. Trans: The Genetic Structure of Populations, Springer-Verlag, 1974.
- Kingman, J. F. C. 2000. Origins of the Coalescent: 1974-1982. Genetics, 56: 1461-1463.
- Kelly, F. P. 2011. Reversibility and Stochastic Networks. Cambridge, Cambridge University Press.
- Lewontin, R. C. 1967. The Principle of Historicity in Evolution. In: Paul S. Moorehead and Martin Kaplan, eds., Mathematical Challenges to the Neo-Darwinian Interpretation of Evolution. Philadelphia: Wistar Institute Press, pp. 81-94.
- Li, C. C. 1955. Population Genetics. Chicago: University of Chicago Press.
- Longo, G. and Montévil, M. 2014. Perspectives on Organisms: Biological time, symmetries and singularities. Coll. ‘Lecture notes in morphogenesis’. Springer
- Malécot, G. 1948. Les mathématiques de l’hérédité. Paris, Masson.
- Matthen, M. and Ariew, A. 2009. Selection and Causation. Philosophy of Science, 76: 201-224.
- Montévil, M. and Mossio, M. 2015. Biological organisation as closure of constraints. Journal of Theoretical Biology, 372: 179-191.
- Price, G. R. 1972. Fisher’s ’fundamental theorem’ made clear. Annals of Human Genetics, 36, 129-140.
- Roughgarden, J. 1979. Theory of Population Genetics and Evolutionary Ecology: An Introduction. New York: MacMillan Publishing Co.
- Simon H. 1977, Models of Discovery. Springer-Verlag.
- Simpson, G. G., 1964. This View of Life. New York: Harcourt, Brace and World.
- Sober, E. 1984. The Nature of Selection. Cambridge (MA): MIT Press.
- Sober, E. 1997. Two Outbreaks of Lawlessness in Recent Philosophy of Biology. Philosophy of Science, 64, Supplement. Biennial Meetings of the Philosophy of Science Association. Part II: Symposia Papers (Dec., 1997), S458-467.
- Walsh, D., Ariew, A. & Lewens, T, 2002. The Trials of Life: Natural Selection and Random Drift. Philosophy of Science, 69: 452-473.
- Watterson, G. A. 1976. Reversibility and the Age of an Allele. I. Moran’s infinitely Many Neutral Alleles Model. Theoretical Population Biology, 10: 239-253.
- Watterson, G; A. 1977. Reversibility and the Age of an Allele. II. Two-allele Models, with Selection and Mutation. Theoretical Population Biology, 12: 179-196.
- Weber, J.S., Depew, D. & Smith, J.D. eds., 1988. Entropy, Information and Evolution. Cambridge (MA): The MIT Press.
- Weinberg, N. 1908. Ueber den Nachweis der Vererbung beim Menschen. Jahreshriften des Vereins für Vaterländische Naturkunde in Württemburg, 64: 368-382. Translated in: Papers in Human Genetics, ed. S. H. Boyer (1963), p. 4-15, Englewood Cliffs, NJ: Prentice-Hall.
- Williams, G. C. 1992. Natural Selection: Domains, Levels and Challenge., New York, Oxford University Press.
- Wright, S. 1921. Sytems of mating. Genetics, 6: 111-178.
- Wright, S. 1937. The distribution of gene frequencies in populations. Proceedings of the Natinal Academy of Science, 23: 307-320.
- Wright, S. 1940. The statistical consequences of Mendelian heredity. In The New Systematics, ed. J. Huxley. Oxford: Clarendon, p. 161–183.