Répétition et réversibilité dans l’évolution : La génétique des populations théorique

Répétition et Réversibilité dans l’Évolution: La génétique des populations théorique

Jean Gayon ∗ and Maël Montévil †

∗ Université Paris I Panthéon-Sorbonne

† Université Paris 7 Diderot

Abstract

La répétitivité et la réversibilité ont longtemps été considérées comme des traits caractéristiques de la connaissance scientifique. Dans la génétique des populations, la répétitivité est illustrée par un certain nombre d'équilibres réalisés dans des conditions spécifiques. Étant donné que ces équilibres sont maintenus en dépit du renouvellement des générations (réarrangement de gènes, reproduction...), on peut légitimement dire que la génétique des populations révèle d'importantes propriétés d'invariance par transformation. La réversibilité est un sujet plus controversé. Ici, le parallèle avec la mécanique classique est beaucoup plus faible. La réversibilité est incontestable dans certains modèles stochastiques, mais au prix d'un concept probabiliste particulier de réversibilité. Par contre, elle ne semble pas être une propriété de la plupart des modèles déterministes classiques décrivant la dynamique des changements évolutifs au niveau des populations. Nous distinguons plusieurs sens de la « réversibilité ». En particulier, la symétrie par inversion du temps ne doit pas être confondue avec la rétrodiction.

1. Introduction

Les biologistes de l’évolution supposent souvent que « l'évolution est unique et irréversible ». Dans la littérature contemporaine, cette affirmation est souvent étroitement liée à l'affirmation selon laquelle l'évolution, historiquement contingente à tous points de vue, est dépourvue de lois et de théories authentiques. Bien que nous partagions l'affirmation de John Beatty suivant laquelle toutes (ou presque toutes) les généralisations en biologie sont historiquement contingentes[1], nous pensons que l'affirmation « l'évolution est unique et irréversible » est beaucoup trop générale et trop vague pour être satisfaisante. En réalité, la biologie contemporaine propose des exemples significatifs de répétition, d’invariance, et de réversibilité, tant sur le plan théorique qu’au niveau expérimental. Ces exemples peuvent aider à sortir de l'alternative trop étroite entre « contingence historique » et « lois » en biologie de l’évolution. Cette alternative souffre de son excessive radicalité philosophique. Les oppositions entre répétabilité et non-répétabilité et entre réversibilité et irréversibilité appliquées aux phénomènes évolutifs sont utiles pour nuancer ce débat. Il est possible que la répétabilité et la réversibilité de l'évolution soient marginales ; néanmoins il en existe des exemples clairs tant sur le plan théorique qu’expérimental. Dans ce texte, nous limitons notre analyse au cas de la génétique des populations théorique.

Que signifient exactement les termes « répétabilité » et « réversibilité »? La définition en est délicate, surtout dans le second cas. La réversibilité de l'évolution signifie-t-elle qu'une entité en évolution (par exemple une population ou une espèce) peut revenir à un état antérieur, par n’importe quelle trajectoire, ou que la trajectoire inverse doit être strictement symétrique de la trajectoire directe ? Dans ses travaux sur l'irréversibilité de l'évolution, le paléontologue belge Louis Dollo était particulièrement préoccupé par ce dernier sens de «réversibilité». Selon Dollo, pour que l'évolution soit réversible, il faut admettre que les causes qui ont donné lieu aux variations individuelles à la source de la transformation initiale et à leur fixation puissent intervenir dans un ordre strictement inverse (Dollo 1913, cité par Gould 1970, p. 199). Une autre difficulté provient des notions techniques de réversibilité définies en mathématiques et en physique. Ces notions sont-elles applicables à la biologie de l’évolution ? L'un des principaux objectifs de ce chapitre est de clarifier les différents sens de répétition et réversibilité applicables à l'évolution. La répétition est une question plus simple, mais cette notion implique également une certaine ambiguïté.

Louis Dollo a introduit sa fameuse « loi de l'irréversibilité dans l'évolution » dans les termes suivants : « ... Un Organisme ne peut retourner, même partiellement, à un état antérieur déjà réalisé dans la série de ses ancêtres » (Dollo 1893). Comme le suggère cette formule, Dollo était intéressé par le problème de la réversibilité au niveau de l'organisme ou au moins d'un organe complexe. En outre, comme paléontologue, il a conçu sa « loi » comme s’appliquant à grande échelle temporelle (macroévolution en termes modernes). Dollo ne nie pas que des inversions puissent se produire à des niveaux plus élémentaires ; en outre la génétique n’existait pas encore. Au regard des connaissances actuelles, il vaut la peine d’examiner les questions de l'invariance et de la réversibilité à un niveau microévolutif.

La répétitivité et la réversibilité de l'évolution peuvent être considérées aux niveaux empirique ou théorique. Au niveau empirique, les objets vivants présentent des propriétés d'invariance qui sont cruciales pour l’évolution, tels que la réplication des gènes, la constance du nombre de chromosomes dans la mitose ainsi que l’alternance des générations au niveau de l'organisme. Dans de tels cas, l'invariance n’est pas absolue, en effet la réplication du matériel génétique n’est pas parfaite et le matériel héréditaire présente une capacité au changement (mutation, recombinaison,...). De même, la reproduction connaît des accidents (par ex. des anomalies de développement) et existe sous divers modes (asexuée ou sexuée, par exemple). La réplication et la reproduction sont des propriétés très générales des êtres vivants, et fournissent une base pour les modèles d’évolution. Bien sûr, elles résultent d'un processus historique, et pour cette raison elles ne peuvent pas être pensées comme des « lois de la nature » au sens d’énoncés universels de portée illimitée. L'un d’entre nous a préconisé l'utilisation de la notion de contrainte afin d’appréhender l'invariance restreinte dans le contexte de l'historicité biologique (Longo & Montévil 2014, Montévil & Mossio 2015).

Les généticiens des populations partagent également une notion intuitive de réversibilité. Certains processus biologiques rendent le retour d'une population à un état antérieur possible : mutations inverses, rétro sélection (coefficients de sélection inversés), et le hasard (dérive aléatoire), le permettent. Ce que « réversibilité » signifie précisément dans ces exemples est une question ouverte, mais l'idée que les populations puissent revenir à un état antérieur est parfaitement plausible compte tenu de la nature des processus biologiques fondamentaux impliqués dans l'évolution génétique. Il existe une autre façon de formuler la notion intuitive de réversibilité, à savoir : « pour un individu donné, on peut considérer l'ensemble de tous les états possibles de son génome. On passe d'un état à un autre moyennant les sources de changement génétique [...]. Il est clair que toute suite quelconque d'états E1, E2... Ei... Ek qui peut être parcourue dans un sens par un individu donné, peut également, théoriquement, être parcourue dans l’autre sens. » (Goux 1979, p. 568).

Ces notions intuitives de répétitivité et de réversibilité viennent avant la construction de modèles en génétique des populations. Elles doivent être soigneusement distinguées des propriétés découvertes par le développement de modèles décrivant l'évolution génétique des populations. À ce niveau, des notions non-triviales de répétitivité et la réversibilité apparaissent ; elles résultent de la modélisation elle-même. La section 2 montre comment les modèles de génétique des populations satisfont une caractéristique des connaissances scientifiques rencontrée dans le domaine des sciences physiques, à savoir des propriétés formelles d'invariance par transformation. La section suivante examine si la génétique théorique a aussi la capacité de mettre en évidence des propriétés de réversibilité ou non. Ceci est un problème plus difficile. Après avoir défini plusieurs significations possibles de la réversibilité, la section 3 montre que la réversibilité dans le sens mathématique est illustrée par certains modèles stochastiques, alors que des modèles déterministes classiques ne présentent pas cette propriété. La conclusion soulève de sérieux doutes sur la comparaison traditionnellement faite entre mécanique classique et modèles déterministes en génétique des populations.

2. Répétitivité en génétique des populations théorique

Jean-Michel Goux observe que la répétitivité sans fin du cycle de vie est la source d'un certain nombre d'équilibres en génétique des populations (1979, p. 567). Nous développons ici librement cette proposition. En dépit de son utilisation sophistiquée en mathématiques, la notion d'invariance par transformation peut être définie de manière simple et générale et peut être appliquée à de nombreux domaines de connaissance au delà des mathématiques et de la physique théorique. Pour une classe donnée d'objets, un invariant est une propriété qui demeure inchangée lorsqu’un type de transformation est appliquée à ces objets. Ce concept est particulièrement fructueux lorsque les objets et leurs relations sont décrits par des formules mathématiques, un sens précis peut alors être donnée à ce qui est considéré comme invariant.

L'un des exemples les plus célèbres d'invariance en physique concerne les transformations galiléennes. Dans sa formulation traditionnelle en mécanique classique, le principe d’invariance de Galilée (également appelé principe de relativité galiléenne) affirme que les lois du mouvement sont les mêmes dans tous les référentiels inertiels.

Les invariances par transformation peuvent être de plusieurs types. En mécanique classique et relativistes, elles sont liées à un mouvement. Cependant, elles peuvent également être par rapport à des structures (à savoir la composition d'une classe particulière d'objets). Cette section examine le cas de l'invariance de la structure génétique d'une population sous certaines conditions. Les exemples d'équilibres génétiques que nous donnons ci-après appartiennent à ce qu'on pourrait appeler la statique de l'évolution, par opposition à la dynamique évolutive. La réversibilité est un cas extrême d'invariance par transformation. Cette notion sera discutée dans la partie 3.

L'équilibre de Hardy-Weinberg est certainement l'exemple le plus connu d'un invariant structurel. Considérons un seul locus avec deux allèles A et a de fréquence p et q (avec p+q=1)[2]. La loi d’Hardy-Weinberg stipule que, quelles que soient les fréquences initiales des gènes et les fréquences initiales des génotypes, si [1] tous les croisements se produisent au sein de la même génération (pas de chevauchement entre les générations), s'il n'y a [2] pas de sélection, [3] pas de migration, [4] aucune mutation, si [5] le choix de partenaire est aléatoire, et si [6] la taille de la population N est assez grande pour que 1 /N ≈ 0, alors les fréquences des génotypes sont constantes et dépendent seulement des fréquences de la génération initiale (voir Jacquard 1970, p. 48-58, et Hartl, 1980, pp. 93-94). Sous ces conditions, les fréquences des génotypes sont AA : p2 ; Aa : 2pq ; aa : q2. Dans une population à générations discrètes, la population atteint immédiatement ces proportions après la première génération de croisement, et les rapports attendus restent constants tant que les six conditions mentionnées sont satisfaites. Certains auteurs en font un «principe» (Crow et Kimura 1970). La loi de Hardy et Weinberg est néanmoins un théorème, car elle peut être démontrée sur la seule base de la loi mendélienne de ségrégation et des six conditions énoncées ci-dessus. On parle aussi d’« équilibre de HW », où « l'équilibre [réfère] au fait qu'il n'y a aucune tendance à ce que la variation provoquée par la coexistence des différents génotypes disparaisse » (Edwards, 1977, p. 7). La raison pour laquelle cette loi est si importante est qu'elle exprime seulement l'effet de l'hérédité mendélienne. Comme Edwards le dit, «cette capacité à maintenir la variation génétique est l'un des aspects les plus importants de la génétique mendélienne» (ibid.). La constance des fréquences génétiques sous hérédité mendélienne fournit un modèle de référence pour décrire l’effet des «forces» de l'évolution telles que mutation, migration, sélection, etc., susceptibles de modifier la structure génotypique de la population. En revenant au problème de la répétitivité, l'équilibre HW est typiquement un invariant par transformation car il identifie quelque chose (la distribution des gènes et des fréquences génotypiques) qui persiste en dépit de la redistribution indéfinie des allèles qui se dissocient par méiose à chaque génération. Bien sûr, la loi HW est une idéalisation, car aucune population réelle ne satisfait jamais strictement les conditions qui permettent sa dérivation.

Un autre exemple classique d'invariance structurelle sous transformation en génétique des populations est le « principe de Wright », aussi appelé « loi d'équilibre de Wright ». Ce principe donne la distribution des fréquences des génotypes dans une population infinie, pour un locus diallélique[3]:

(p2+Fpq) + 2pq(1-F) + (q 2+Fpq) = 1

où F représente le coefficient de consanguinité. Cette loi exprime les proportions zygotiques[4] attendues dans une population avec une certaine quantité de consanguinité, autrement dit une population où des partenaires sont plus étroitement liées que s’ils étaient choisis au hasard. L'équilibre de Hardy-Weinberg est en fait un cas particulier de l'équilibre de Wright, correspondant à F = 0. Par conséquent, la loi de l'équilibre de Wright prend en compte l'une des principales causes d’écart relativement à l'équilibre HW (l'autre étant l’homogamie). Le coefficient F peut évidemment changer. Néanmoins, la formule de Wright indique que, pour un F donné, et si aucun autre facteur ne modifie les fréquences génotypiques, la structure génétique de la population est invariante de génération en génération. En dehors de la loi de Hardy-Weinberg et de l’article de Fisher sur la corrélation entre parents sous hérédité mendélienne (Fisher 1918), c'est l'un des résultats les plus anciens de la génétique des populations théorique. Il a été démontré à plusieurs reprises, et amélioré et généralisé (multi-allélisme) depuis le papier original de Wright en 1921 (Wright 1921; Malécot 1948; Li 1955).

Comme dit précédemment, l'équilibre HW est établi dès la première génération de croisement. Mais cela n’est vrai que si les générations ne se chevauchent pas (voir ci-dessus: condition 1). Si les générations se chevauchent, il faut plus de temps pour atteindre l'équilibre HW, mais la population converge vers cet équilibre. Par conséquent, l'équilibre n’est pas immédiat; il est le résultat d’une « tendance ».

Cette notion de tendance est omniprésente en génétique des populations. Sur la base d’une idée suggérée par J. B. S. Haldane, Crow et Kimura parlent de «Statique évolutionniste», par opposition à «la dynamique de l'évolution». Dans un article intitulé «la statique de l'évolution», Haldane (1954) affirme que, bien que l'évolution soit un «processus dynamique», une bonne partie de celle-ci est mieux comprise en termes de «statique». Pour Haldane, l'évolution est en général un processus extrêmement lent, qui peut néanmoins compter sur des forces puissantes (en particulier de sélection). Donc une part importante des processus évolutifs doit être pensée en termes d’équilibres approximatifs résultant d'un équilibre de «forces» en conflit les unes avec les autres : équilibre entre mutation directe et mutation inverse, équilibre entre migration et dérive, équilibres sélectifs, etc. Voir Crow & Kimura 1970, 256-296)[5]. La «statique» de l'évolution est l'une des parties les plus spectaculaires de la génétique des populations théorique. Souvent, les résultats sont simples, élégants et faciles à trouver, contrairement à la «dynamique». Pour cette raison, les formules d'équilibre jouent un rôle important dans l'enseignement élémentaire de la génétique des populations.

La découverte de propriétés formelles d'invariance par transformation est une composante importante des connaissances scientifiques, que ce soit en biologie, en physique ou en économie. Dans Models of Discovery, Herbert Simon a écrit que «la notion d'invariance par transformation, comme condition nécessaire pour qu’une propriété d'un système physique soit ‘réelle’, a fourni une motivation de premier plan pour le développement de la mécanique relativiste et d'autres branches de la physique» (Simon, 1977, p. 79, n. 8). Nous ne devrions pas être surpris de trouver ces invariants dans la théorie évolutionniste. Comme indiqué précédemment, la répétitivité est une propriété empirique importante des êtres vivants : répétitivité des cycles de vie, répétitivité de la reproduction cellulaire, répétitivité de la réplication des gènes, répétitivité des phénomènes occasionnels tels que les mutations récurrentes au niveau de la population. Étant donné que les phénomènes répétitifs sont si largement observés à un niveau élémentaire, il est raisonnable de penser que des invariants plus formels émergent lorsque la génétique des populations extrapole le comportement des populations à partir de ces cas empiriques de répétitivité. Comme suggéré dans l'introduction, le degré considérable d'historicité et de contingence dans l'évolution n’est pas opposé à ce qu’il existe des «lois», au moins au niveau microévolutif.

3. Réversibilité par rapport au temps

La réversibilité est une notion moins évidente que l'invariance par transformation, pour deux raisons. Tout d'abord, il s'agit de problèmes techniques et parfois contre-intuitifs. Deuxièmement, les biologistes de l'évolution utilisent différentes notions de réversibilité, et très souvent le font implicitement. En discutant de la réversibilité du temps avec plusieurs généticiens des populations, nous avons été frappés par la combinaison de certitude spontanée et de doute dans leurs réactions. En fait, il semble qu’il n’y ait pas de consensus clair. Cette section vise à clarifier les différentes significations possibles de «réversibilité» en génétique des populations.

Trois sens différents de «réversibilité» se trouvent dans la littérature, principalement mathématique et physique. Après avoir donné leurs définitions, nous évaluerons leur applicabilité à la génétique des populations.

3.1 Trois sens de ‘réversibilité’

Pour traiter correctement de la réversibilité en tant que concept opérationnel en mathématiques, en physique et dans d'autres sciences exactes, il faudrait une analyse plus formelle et détaillée. Les remarques qui suivent esquissent des distinctions qui visent à clarifier le problème de la réversibilité en génétique des populations[6].

3.1.1 Retrodictabilité

Dans la mécanique classique, la prédiction et la rétrodiction sont symétriques: en connaissant la ou les lois régissant la dynamique d'un phénomène et l'état du système à un temps t, il est possible de déduire l'état du système à tout autre temps, passé ou futur. Ce qui est requis pour la rétrodictibilité est la possibilité de dériver une équation inversée de l'équation directe qui décrit la trajectoire inverse aussi précisément que l'équation directe décrit le mouvement normal. Pour une telle inférence, le cadre théorique de l'astronome n'a pas besoin d'être parfait. Il peut avoir, et a certainement ses propres limites (par exemple un comportement chaotique). Néanmoins, dans le cas d'équations différentielles, la prédiction et la rétrodiction sont également possibles; notons également que, pour les modèles en temps discret, la rétrodictibilité peut parfois être impossible alors que le modèle est déterministe (voir Gayon & Montévil 2017). La rétrodictibilité est souvent confondue avec la réversibilité du temps au sens mathématique (voir ci-dessous), et les deux notions peuvent en effet être étroitement liées dans des cas particuliers mais elles sont distinctes. En raison des confusions entre rétrodictibilité et la réversibilité, parler de la rétrodiction (inférence quant au passé) comme un cas de «réversibilité» devrait sans doute être évité. Bien que ce ne soit pas une utilisation courante, le reste de ce texte distingue à plusieurs reprises la «réversibilité» et la rétrodictibilité.

3.1.2 La réversibilité par rapport au temps au sens «mathématique» conventionnel

La notion de réversibilité repose sur une comparaison entre les trajectoires normales et les trajectoires après un renversement de temps, c'est-à-dire où le passé devient le futur et le futur devient le passé. La réversibilité se produit lorsque ces deux trajectoires suivent la même loi. À l'inverse, lorsque la dynamique est irréversible, la loi donne une orientation du temps (la flèche du temps). La question de la réversibilité en ce sens est communément abordée en physique théorique.

D'un point de vue technique, les équations décrivant la dynamique d’un processus symétrique par inversion du temps sont invariantes si le signe du temps est inversé. En d'autres termes, si t est remplacé par -t, la loi régissant le phénomène ne sont pas affectées. Dans le cas de la mécanique classique, cela résulte de la loi de Newton qui donne l’équation du mouvement d 2x / dt2 = F(x). On voit facilement que la substitution de t par -t dans cette équation ne change rien. La même «loi» s’applique dans les deux sens du temps. Cela signifie que, si une balle est lancée, la loi régissant le mouvement de la balle montante est identique à la loi qui décrit le mouvement de la balle descendante. La direction de la trajectoire sera inversée, bien sûr, et la vitesse diminue au lieu d'augmenter, mais le taux de diminution sera strictement le même que le taux d'augmentation. L’équation d 2x / dt2 = F(x) n'est pas affectée par une inversion du temps. Dans ce sens précis, la réversibilité du temps est traditionnellement considérée comme une propriété presque universelle de la mécanique classique. Il convient toutefois de noter que la loi de Newton est réversible si et seulement si F est symétrique par inversion de temps, par exemple lorsque F ne dépend que de x ou du produit de deux vitesses. C'est le cas pour toutes les forces fondamentales classiques : la gravitation et l'électromagnétisme. Cependant, dans d'autres cas, comme le frottement, où F(dx/dt) = -fdx / dt (où f est le coefficient de frottement), la loi n'est plus réversible.

Les notions de réversibilité et de rétrodictibilité peuvent être étroitement liées dans des cas particuliers. Par exemple, la loi de Newton abordée plus haut permet la rétrodictibilité et la réversibilité. Cependant, les deux notions ne sont pas nécessairement associées. Considérons le cas des équations en temps discret, qui sont particulièrement importantes dans la génétique des populations. La fonction permettant une «prédiction du passé» peut être totalement différente de la fonction qui décrit comment le système passe de t à t+1. Considérons une équation de récurrence de la forme p(t+1)=g[p(t)]. Nous pouvons définir la rétrodictibilité:

où h est une fonction obtenue à partir de g et permet la rétrodiction. Les fonctions h et g peuvent être totalement différentes.

La réversibilité signifie au contraire que h=g. Ceci signifie que la transition de t à t +1 et celle de t +1 à t suivent la même règle.

Enfin, il existe une autre raison importante pour laquelle la rétrodictibilité et la réversibilité ne doivent pas être confondues. Jusqu'à présent, la réversibilité du temps n'a été discutée que dans le contexte de processus déterministes. Cependant, la réversibilité du temps peut également être une propriété des processus stochastiques : si les propriétés stochastiques d'un processus dépendent de la direction du temps, ce processus est considéré comme irréversible; s'ils sont identiques pour les deux sens du temps, le processus est dit réversible.

Cette notion statistique de réversibilité a été appliquée avec succès à un certain nombre de sujets, tels que les réseaux de files d'attente, les processus de migration, et la génétique des populations, où les processus markoviens sont extrêmement importants pour le traitement de la dérive génétique aléatoire (Kelly 2011). Contrairement à la réversibilité dans les systèmes déterministes, la réversibilité stochastique est difficilement compatible avec la rétrodictibilité. La rétrodictibilité est habituellement comprise comme la possibilité de reconstituer la trajectoire actuelle qui a conduit à l'état actuel et est fortement associée au déterminisme, ou du moins à l'idée d'une séquence causale qui a conduit la trajectoire. La notion de rétrodictibilité pourrait éventuellement être étendue aux processus stochastiques, mais ce n'est pas la manière habituelle de penser à ce sujet.

En résumé, bien que simple en principe (insensibilité d'une loi donnée à l'inversion temporelle), la notion «mathématique» de la réversibilité est délicate. Elle n'est pas synonyme de rétrodictibilité, et s'applique au delà des situations déterministes.

3.1.3 La notions ‘physique’ ou ‘thermodynamique’ d’irréversibilité

La notion «physique» de réversibilité est étroitement liée à la thermodynamique. La réversibilité «physique» signifie qu'un système physique peut spontanément revenir à un état physique antérieur. Un exemple classique est le cas d’un ressort qui revient à son état antérieur après avoir été allongé. En revanche, nous ne nous attendons pas à ce qu'un verre brisé retrouve spontanément sa forme originelle. La notion physique traditionnelle de réversibilité est étroitement associée à la thermodynamique : l'évolution réversible d'un système est un processus où aucune entropie n'est produite. À l'inverse, plus il y a production d’entropie, plus le processus est irréversible. Dans un système fermé, l'entropie est une quantité qui ne peut qu’augmenter. Pour les besoins du présent chapitre, il suffit de noter que les notions physiques de réversibilité et d'irréversibilité sont étroitement liées à celles des systèmes conservatifs ou dissipatifs, ces derniers impliquant une production d’entropie

Du point de vue thermodynamique, les phénomènes biologiques sont largement considérés comme des processus loin de l'équilibre: ils conservent une entropie relativement faible du fait des flux de matière et d’énergie qui les traversent ; mais parce qu’ils produisent de l’entropie, ils sont irréversibles du point de vue thermodynamique. Cependant, cet aspect concerne la dispersion de l'énergie dans un espace de positions et de moments, qui est différent de l'espace des populations de gènes que nous discutons dans cet article. En conséquence, l'irréversibilité thermodynamique est analytiquement indépendante de la question de l’(ir)réversibilité intrinsèque des modèles de génétique des populations.

3.2 Rétrodictibilité et réversibilité en génétique des populations

Appliquons ces notions à la génétique des populations. La présente analyse sera limitée à quelques cas typiques.

3.2.1 Processus stochastiques

Les processus stochastiques offrent probablement le cas le plus spectaculaire de réversibilité temporelle dans le sens mathématique le plus strict, c'est-à-dire l'insensibilité d'un modèle donné au renversement du temps. Ceci est explicite dans deux articles de G.A. Watterson (1976 et 1977). Ces articles considèrent la distribution de probabilité de l'âge d'un allèle mutant, dont la fréquence actuelle est connue. L'âge d'un allèle est défini comme le temps écoulé entre l'introduction de l'allèle par mutation et le présent. Dans le premier article (1976), l'auteur suppose qu'il n'y a ni mutation ni sélection. Le modèle est en temps discret et discute la dérive génétique aléatoire. La méthode consiste à considérer y, la fréquence actuelle du gène mutant, comme « l'état initial d'un processus stochastique, et à étudier la durée de la diffusion pour atteindre l'état x (ou l'état 0) pour la première fois » (x étant la fréquence à t unités de temps avant le présent). Watterson est très explicite quant au rôle de la réversibilité dans son modèle, dont l'esprit général est présenté dans les termes suivants :

“Cette interprétation semble surprenante à deux niveaux : d'abord, parce que cela signifie que les résultats publiés sont simplement un temps d'extinction pour la diffusion ; deuxièmement, il existe des processus stochastiques pour lesquels cette réversibilité est valide, c'est-à-dire des processus dont le comportement vers le passé est statistiquement identique à leur comportement futur.” (Watterson 1976, p. 240)

Cette affirmation est accompagnée d'une figure non moins explicite (figure 1), illustrant la symétrie entre l'âge d'un allèle et le temps d'extinction.

Le modèle lui-même repose sur une estimation des probabilités de toutes les transitions possibles d'un état à l'autre, dans les deux sens du temps (β→ β’ et β’→ β). Étant donné que la chaîne de Markov considérée a une distribution stationnaire, cela signifie que le processus décrit est réversible (Kelly 2011).

La conclusion principale de Watterson est que «... la répartition par âge {Pi (a)} pour un allèle maintenant représenté par les gènes i dans la population est la même que la distribution du temps d'extinction pour un tel allèle.» (Ibid., p. 246). Ce résultat remarquable illustre l'utilité de la réversibilité temporelle pour l'élaboration de modèles en génétique des populations : «Par réversibilité, on entend que compte tenu de l'état actuel d'un processus stochastique, les propriétés statistiques de son comportement futur sont les mêmes que celles de son histoire passée, traitée comme un processus stochastique avec un temps s’écoulant en sens inverse.» (Watterson 1977, p. 179)

Dans le même esprit, la réversibilité du temps a été largement utilisée dans la théorie de la coalescence, qui a probablement été l'innovation majeure en génétique des populations depuis les années 1980 (Kingman 2000).

3.2.2 Processus déterministes

La génétique de la population est généralement divisée en deux branches principales. La première est la théorie stochastique, qui met l'accent sur l'effet des changements aléatoires, en particulier la «dérive aléatoire», dans les fréquences alléliques et génotypiques. La seconde met l'accent sur les effets «déterministes» de facteurs tels que la mutation, la migration, la sélection et le système de reproduction. La théorie déterministe de la génétique des populations ignore les changements aléatoires et est donc moins complète que la théorie stochastique (Ewens 2012). En fait, tous les processus réels incluent un aspect stochastique, notamment parce que les populations réelles sont finies et sujettes à dérive aléatoire. Par conséquent, dans le monde réel, les facteurs déterministes interagissent toujours avec des facteurs stochastiques. En outre, lorsque les généticiens des populations parlent des facteurs évolutifs en termes de «forces», il s’agit d’une métaphore. Certains philosophes défendent que la génétique des populations ne traite pas de forces mais d’effets statistiques (Matthen et Ariew 2009). Néanmoins, la notion de facteurs «déterministes» dans la génétique des populations est acceptable au sens de facteurs ayant un effet directionnel et tendant à « pousser » les fréquences génétiques et génotypiques dans une direction. L'importance de ces «facteurs déterministes» a conduit J.B.S. Haldane à dire que la génétique des populations – en particulier la théorie génétique de la sélection naturelle – constitue une «mécanique de l'évolution». C'est en effet une métaphore tentante, que l'un des auteurs a approuvé dans le passé (Gayon 1998, chap. 8). Cependant, la question de la réversibilité des équations nous conduit à une réserve importante quant à cette analogie.

3.2.2.1 Retrodictabilité

Nous considérerons d’abord la question de la rétrodictibilité. Intuitivement, si l'existence de modèles déterministes en génétique des populations est acceptée, la réponse semble évidente. R. Lewontin est particulièrement clair sur cette question: «Si je vous donne juste l’histoire d'une population déterministe, je peux tout dire sur son passé, précisément parce que cette histoire est déterministe» (Lewontin 1967, p. 87). C'est exactement ce que signifie la rétrodictibilité.

Les manuels de génétique des populations sont remplis de modèles déterministes décrivant les effets sur les fréquences génétiques et/ou génotypiques, de facteurs tels que mutations récurrentes, migration, sélection, etc. Dans ces modèles, le temps peut être soit discret, soit continue. En temps discret, l'unité de temps est une génération, et la dynamique évolutive de la population est décrite par des équations de récurrence. En temps continu, les générations se chevauchent et le changement est supposé continu. La méthode de base repose alors sur des équations différentielles. R. Fisher a préféré cette méthode, qui est généralement appropriée pour l'espèce humaine. En fait, la typologie des modèles par rapport au temps est un peu plus compliquée (voir Crow et Kimura 1970, chap. 1), mais on négligera ici ces complications.

La rétrodictibilité semble être une propriété générale des modèles déterministes de la génétique des populations. Dans certains cas, les équations de récurrence ne peuvent pas être inversées car un état a plusieurs antécédents, générant une ambiguïté pour la rétrodiction. Nous discuterons maintenant deux exemples de rétrodictibilité.

Premièrement, le cas d'une population soumise à une mutation récurrente à sens unique. L'effet de mutation récurrente sur la fréquence du gène muté est:

où u est la probabilité qu’un allèle ‘normal’ A de fréquence p mute en a.

Comme 1-u est la probabilité que A ne mute pas, [2] exprime que p au temps t+1 est la fraction des allèles A ne mutant pas (Roughgarden 1979, p. 43-45). L’équation [2] conduit à:

Chaque génération augmente l’exposant de 1-u : comme 1-u<1, la fréquence d'un gène diminue à un rythme qui diminue lui-même, car la quantité d'allèles A dans la population est réduite à chaque génération. Ce processus déterministe est représenté dans la figure 2 pour p(0) = 0,9, et diverses valeurs pour la pression de mutation u. La possibilité même de tracer une telle courbe suggère fortement que le phénomène est à la fois prédictible et rétrodictible.

Le terme au numérateur est la valeur sélective WA de l’allèle A (valeur sélective moyenne de tous les génotypes comprenant A). Le dénominateur est la valeur sélective moyenne de la population W (moyenne des valeurs sélectives des différents génotypes pondérés par les fréquences de ces génotypes). L'équation [4] peut ainsi être écrite:

Cette équation est non-linéaire. Sauf cas particuliers, il n'existe pas de méthode générale pour l'itérer de façon analytique, mais cela peut être fait avec un ordinateur. La Figure 3 donne le résultat d'itérations informatiques de [4] pour la sélection contre un allèle récessif avec une forte sélection. Ceci est une illustration d'un processus typiquement déterministe.

Il est possible d’écrire p(t)=h(p(t+1)) et d'itérer cette relation pour remonter d’une génération à la précédente (Gayon & Montévil, 2017). Notez que h est dérivée de l'équation par récurrence [4]. La question de la forme de h nous amène à la question de la réversibilité.

3.2.2.2 Réversibilité par rapport au temps

La question est ici de savoir si les «lois» en génétique des populations sont affectées par un renversement de temps (voir la section 3.1.2). Puisque la notion de «loi» est importante ici, il convient de rappeler la proposition d'E. Sober (1997). Pour lui, le processus d'évolution tel qu'il est étudié dans la génétique des populations «est régi par des modèles qui peuvent être connus pour être a priori vrai». Ces modèles sont des vérités mathématiques, qui décrivent comment les systèmes d’un type spécifié changent dans le temps, d'où l'expression de Sober «loi de processus». Par exemple, compte tenu des lois de Mendel et d'une définition opérationnelle de notions telles que mutation récurrente, valeur sélective, etc., les lois processuelles de la génétique des populations décrivent comment ces facteurs déterminent la trajectoire d'une population dans l'espace des fréquences génétiques. Ce point de vue est suivi ici (Sober 1984, 1997, voir aussi Gayon 2014).

La notion de loi est ici importante parce que la réversibilité du temps n'est pas tant une propriété d'une trajectoire qu’une propriété de la loi qui régit la dynamique. À proprement parler, la propriété de réversibilité ne nous dit rien sur la capacité d'un système donné de revenir à son état antérieur. Ceci n'est pas exclu, mais dépendra des conditions réelles imposées au système. La réversibilité est une propriété de la loi transformant un état présent en un état futur.

En revenant maintenant aux exemples de mutation récurrente et de sélection, nous pouvons nous demander si les «lois» exprimées dans les équations de récurrence sont réversibles.

Cas 1: Mutations récurrentes

Pour commencer, définissons formellement le concept de réversibilité du temps dans un système dynamique dont l'évolution peut être décrite par une équation de récurrence. Nous supposons que l'état d'un système x(t) au temps t est fonction des p états précédents :

La définition de la réversibilité veut que si (x(0), x(1),…, x(T)) est solution de [6], alors la séquence inversée (x(T), alors x(T-1),…, x(0)) est aussi solution de [6].

Considérons l’équation

Les séquences (0, 1, 3, 6, 10, 15) et (15, 10, 6, 3, 1, 0) sont solutions de [7]. Ceci est général, donc [7] est réversible par rapport au temps.

Considérons maintenant l'équation de récurrence décrivant l'évolution de la fréquence p d'un allèle A sujet à une mutation récurrente. Comme on l'a vu plus haut [2], cette équation est:

La séquence (1, (1-u), (1-u) 2) est solution de [2] mais ((1-u)2, (1-u), 1) n’est pas solution de [2] pour u≠0. Nous concluons que [2] n’est pas réversible pour u≠0.

Cependant, nous anticipons une objection. Renverser la direction de la mutation (a→A au lieu de A→a) équivaudrait à «inverser le processus». Mais ce serait un autre processus; parce qu'un paramètre crucial, avec une signification biologique différente (mutation inverse) a été introduit, ce n'est pas la même loi. La modification de la direction de la mutation ne change pas la direction du temps. La «mutation inversée» est un concept biologique, qui ne doit pas être confondu avec la question de savoir si la loi de processus décrivant la diffusion d'une mutation «récurrente» est «réversible» ou non.

Cas 2: Modèles élémentaires de sélection

L'équation de base pour prédire l'évolution des fréquences génétiques pour une sélection diallélique a été donnée en [4]. Cette équation de récurrence conduit à plusieurs situations qualitativement différentes. Dans tous les cas, les valeurs sélectives sont supposées constantes.

avec: pi : fréquence de l’allèle Ai; Wi : valeur sélective moyenne (ou “fitness”) de l’allèle Ai ; W: fitness moyenne.

L'équation [8] revêt une importance fondamentale pour la théorie génétique de la sélection naturelle. Comme souligné par Crow et Kimura (1970, p. 180), elle montre que le taux de variation de la fréquence des gènes est proportionnel à: (1) les fréquences des gènes, pi (1-pi), ce qui signifie qu'un gène très rare ou très commun va changer lentement, quelle que soit la pression de sélection (2) l’excès de fitness de l’allèle Ai par rapport à la moyenne de la population W i–W qui peut être positif ou négatif.

Avant de commenter la réversibilité, une autre notion cruciale doit être introduite. Si les valeurs sélectives sont maintenues constantes, Δpi peut être écrit:

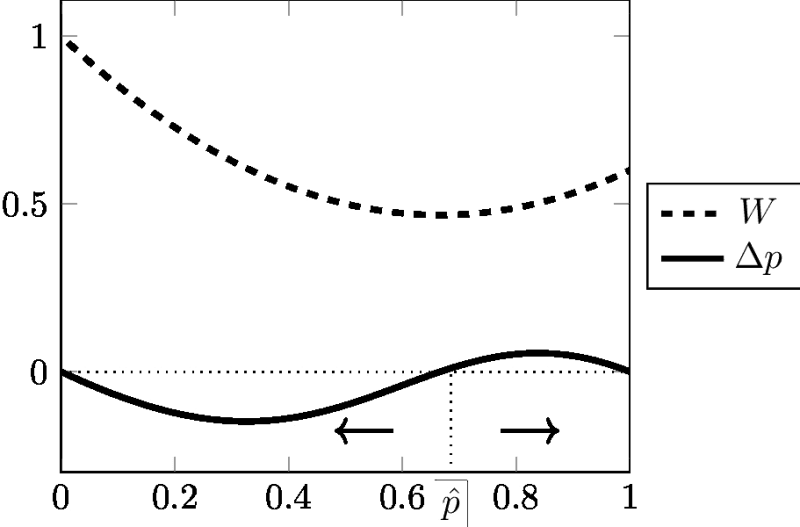
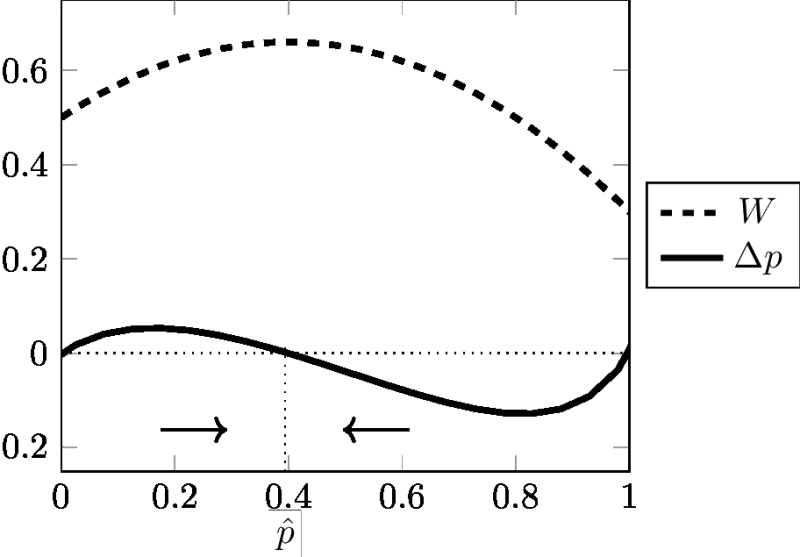
Cette équation célèbre est connue sous le nom de «formule de Wright» (Wright, 1937, 1940). Elle est fondamentale car elle relie le changement de fréquence de gène Δp, avec la pente de la fonction W ( fitness moyenne). Il montre que si W est maximum, alors Δp est nul et la population est à l'équilibre. W est classiquement interprété comme la «fonction de fitness» ou la «topographie adaptative». Comme W tend vers un maximum, une population soumise à sélection est considérée comme «ascendante». Les figures 3 et 4 inspirées d’Albert Jacquard (1971) donnent une illustration graphique du lien entre Δp et W dans deux cas (pour plus de détails, voir Gayon & Montévil 2017). Les flèches dans les figures montrent que W est toujours ≥ 0 et est systématiquement maximisé. L'équilibre est atteint lorsque W est maximal; Cette valeur maximale de W correspond à Δp = 0. Comme l'a observé Roughgarden (1979), il est remarquable que l'équation [9] en dépit d’importantes restrictions (constance des valeurs sélectives), puisse générer tant de trajectoires différentes.

Ces modèles sont-ils réversibles? Supposons par exemple que l'hétérozygote soit avantageux, c'est-à-dire W12 supérieur à W11 et W22. La dynamique de cette sélection est représentée en Figure 4. Si nous inversons les Wij, i.e. si nous remplaçons les Wij par 1/ Wij, alors W12 est inférieur à W 11 et W22. Cela correspond à la dynamique représentée dans la Figure 3 (sous-dominance), avec un équilibre instable et deux équilibres possibles, ce qui est différent de la dynamique initiale. Gayon & Montévil (2017) fournissent une preuve dans le cas particulier d'un modèle diallélique pour W11> W12 > W22. La dynamique de ce système est rétrodictible mais non réversible car la loi inverse fait intervenir une racine carrée. Il est possible de dériver une règle de rétrodiction, mais cette règle est incompatible avec l'idée que la dynamique soit réversible.

Dans le cas haploïde, Gayon & Montévil (2017) montrent que remplacer les valeurs sélectives Wi par les quantités inverse 1/W i dans l'équation de récurrence donne la règle pour le temps inversé. En effet, le calcul montre que la dynamique de l'équation initiale est conservée avec les nouveaux paramètres 1/ Wi. Par conséquent, la «loi» est conservée par un renversement de temps, à condition de changer les constantes. Ce n'est pas une «réversibilité par rappport au temps» au sens strict, mais on peut parler de réversibilité en un sens faible.

En outre, il convient de noter que les modèles standards de sélection avec des valeurs sélectives constantes décrivent des dynamiques qui sont guidées par une fonction maximisée (la valeur sélective moyenne de la population). Par conséquent, il semble difficile d'imaginer que de tels modèles puissent être utilisés pour décrire une transformation inverse obéissant exactement à la même loi: que signifie minimiser W? Cela contredirait les modèles. Pour résumer, tous les modèles élémentaires de sélection évoqués dans le présent chapitre sont déterministes et rétrodictibles, mais ils ne semblent pas décrire un processus réversible dans le temps.

Nous avons mentionné précédemment que, pour des modèles de sélection avec des valeurs sélectives génotypiques constantes, la valeur sélective moyenne augmente toujours de génération en génération jusqu'à ce qu'elle soit égale à zéro lorsque l'équilibre est atteint, donc ΔW≥0. Cependant, cela doit-il être compris strictement ou approximativement? Existe-t-il une marge d'oscillation, en particulier dans le cas de la supériorité des hétérozygotes (voir la figure 4)? L'idée serait alors que la population monte dans la topographie adaptative un peu comme une bille qui descend dans un bol, monte de l'autre côté du bol, etc. Cependant, il a été démontré qu'il n'y a pas d'oscillation (Roughgarden, 1979). Roughgarden note qu'il n'y a aucune possibilité de «dépassements si importants qu’ils puissent empêcher la convergence». Donc W est ≥ 0. Pas d'oscillation, pas de rebond. Ce comportement peut être mis en contraste avec la situation de la mécanique classique. Si un corps mobile trouve un obstacle sur son chemin, on s'attend à ce qu'il communique une fraction de son mouvement à un autre corps et rebondisse. Rien de tel n'est observé dans les modèles de sélection standard: lorsque le point d'équilibre est atteint, le mouvement s'arrête. Ceci est typique d’une dynamique hautement directionnelle où la réversion est à peine concevable tant que les conditions restent les mêmes.

3.2.2.3 Réversibilité 'physique' ou 'thermodynamique'

Il est utile de citer la comparaison que Fisher propose entre son théorème fondamental et le second principe de la thermodynamique:

«Tous deux sont des propriétés de populations ou d'agrégats, indépendamment de la nature des unités qui les composent; tous deux sont des lois statistiques; ils nécessitent l'augmentation constante d'une quantité mesurable, dans l'un des cas l'entropie d'un système physique et dans l'autre la fitness, mesurée par m, d'une population biologique. Comme dans le monde physique, nous pouvons concevoir des systèmes théoriques dans lesquels les forces dissipatives sont totalement absentes et dans lesquelles l'entropie reste constante, afin que nous puissions concevoir, bien que nous ne devions pas nous attendre à trouver, des populations biologiques dans lesquelles la variance génétique est absolument zéro, et dans lesquelles la fitness n'augmente pas.» (Fisher [1930] 1958, p. 39)

Malgré ces ressemblances, l'objectif de Fisher était en fait de souligner les différences entre la Deuxième Loi de la Thermodynamique et son théorème. Parmi les cinq différences qu'il mentionne, une est particulièrement intéressante pour notre sujet, bien que formulée de manière ambigüe: «Par leur irréversibilité, les changements d'entropie sont exceptionnels dans le monde physique, alors que les changements évolutifs irréversibles ne constituent pas une exception parmi les phénomènes biologiques [Entropy changes are exceptional in the physical word in being irreversible, while irreversible evolutionary changes form no exception among biological phenomena]» (Fisher, ibid., P. 40).

En fait, les biologistes modernes, ou du moins certains d'entre eux, comparent l'entropie et la fitness plus littéralement que Fisher. Un exemple stimulant est Lloyd Demetrius, qui propose une adaptation du concept d'entropie à la génétique évolutive et à l'écologie, et présente la notion d'«entropie évolutive»: une mesure de la dispersion de l'âge des ancêtres d'un nouveau-né choisi au hasard. Le concept d'entropie évolutive de Demetrius est une tentative explicite de surmonter la différence évidente entre la physique statistique et la biologie des populations; la physique statistique traite des propriétés de populations de particules inertes, alors que la biologie de la population traite les propriétés des populations d'objets vivants qui se reproduisent. Nous reconnaissons que nous nous sentons plutôt incertains sur le sens précis de l’analogie entre entropie évolutive et l'entropie au sens physique ordinaire. Cette analogie est basée à la fois sur une similitude formelle des équations et sur la distinction entre une description microscopique et une description macroscopique. La proposition stimulante de Demetrius est une façon parmi d’autres de combler l'écart entre la génétique des populations et l'écologie des populations, en mettant l'accent sur la fitness absolue, la densité de la population et la croissance démographique, limitée ou non.

Plutôt que de souligner le genre d'irréversibilité évolutive illimitée que favorise Fisher, Demetrius offre un outil qui laisse place à des processus évolutifs irréversibles (caractérisés par une augmentation unidirectionnelle de l'entropie évolutive) et des processus évolutifs réversibles (ou pratiquement stationnaires). Dans un tel cadre théorique, la distinction réversible / non réversible n'est pas une alternative entre tout et rien, mais plutôt un outil pour décrire la dynamique du changement évolutif (Demetrius 2000).

Ce domaine de recherche est fascinant et novateur, mais demeure spéculatif aujourd’hui. Existe-t-il des analogies réelles avec la friction et la dissipation de chaleur dans les modèles de génétique des populations et d'écologie, ou ces comparaisons ne sont-elles que des métaphores suggestives ou des analogies mathématiques? Cette question sera laissée ouverte.

3.3 Conclusions sur la réversibilité en génétique des populations

Bien que l'analyse ci-dessus reste incomplète, les conclusions qu'elle suggère sont assez simples:

La réversibilité au sens de rétrodictibilité (en fait, une utilisation incorrecte du mot) est courante pour les modèles déterministes, avec des exceptions possibles en temps discret. Elle ne s'applique pas aux modèles stochastiques.

La réversibilité du temps est clairement valide pour certains modèles stochastiques importants; elle semble rare pour les modèles déterministes. Dans un cas (sélection dans une population haploïde), on se rapproche de la réversibilité du temps au prix d’une définition élargie. Toutefois, ce sujet nécessiterait un examen plus exhaustif.

La réversibilité thermodynamique, qui est un sujet fascinant, reste principalement au niveau de la spéculation.

Dans les modèles classiques de sélection, le W sélectif moyen peut difficilement être interprété comme une fonction potentielle.

4. Conclusions

Nous tirons deux grandes conclusions. La première porte sur les lois en biologie de l'évolution. Les lois n'ont pas besoin d'être des énoncés de portée universelle illimitée et empiriquement vrais ; elles peuvent aussi être des « modèles qui peuvent être connus comme vrais a priori » (Sober, 1997). Toutes les vérités mathématiques ne sont pas des lois ; seules le sont celles qui s’élaborent sur la base de situations empiriques plausibles. Par exemple, dans un cadre mendélien, si la mutation, la migration, le système de croisement et la sélection sont des facteurs évolutifs plausibles, il est possible de dériver le comportement typique d'une population soumise à l’action de ces facteurs. Les descriptions abstraites obtenues sont des idéalisations, ni plus ni moins que celles développées par les sciences physiques. La question de savoir si elles sont utiles pour prédire le comportement réel des populations ou non n'est pas pertinente pour leur statut nomologique. Elles disent simplement que, si les conditions C1, C 2,…, Cn sont vérifiées, alors un certain comportement doit être observé. Certains philosophes pourraient faire valoir ici qu'il serait plus sage d'abandonner le terme «loi» et de parler de «modèles». Peut-être est-ce le cas. En pratique, les généticiens de la population utilisent les termes «loi» et «modèle» de façon indifférente pour qualifier l'équilibre HW. Dans d'autres cas, ils ont tendance à préférer le terme «modèle». Nous ne pensons pas que ce soit un problème fondamental. Quel que soit le résultat d'une telle discussion, une conclusion importante de ce chapitre est qu'un nombre impressionnant de résultats de la génétique théorique des populations consiste en des équilibres qui montrent que cette discipline est capable d'identifier des propriétés d'invariance par transformation. La découverte de telles propriétés a été une caractéristique distinctive de la science moderne depuis sa création.

La deuxième conclusion de cette enquête vient limiter la première. La réversibilité du temps a également été considérée comme une caractéristique majeure de la science moderne, avec une référence particulière à la mécanique classique. En génétique des populations, la réversibilité du temps est abondamment présente dans le traitement des processus évolutifs stochastiques. Mais c'est un sens assez particulier de la réversibilité. Dans les limites de cette première enquête exploratoire, la réversibilité en son sens mathématique ne semble pas être une propriété des modèles décrivant les phénomènes déterministes de la génétique des populations ; cettee question devra être examinée de manière plus exhaustive. Les modèles déterministes de la génétique des populations sont hautement rétrodictibles, mais cette propriété n'est pas identique à la réversibilité.

La réversibilité du temps est une propriété très impressionnante des équations de la mécanique classique dans le cas des forces fondamentales. Dans la mécanique classique, les objets suivent le principe d'inertie, de sorte qu'un mouvement rectiligne uniforme ne nécessite pas de cause externe. La structure des modèles de sélection en génétique des populations est différente. Les changements dans une population sont directement influencés par les différences de fitness. Si ces différences cessent, les changements s'arrêtent immédiatement. En ce sens, la sélection en génétique des populations est plus proche d'une mécanique aristotélicienne mathématisée que de la mécanique classique. Dans la mécanique classique, l'énergie est conservée et est transférée de l'énergie potentielle à l'énergie cinétique et vice versa, ce qui garantit la réversibilité temporelle de la dynamique. Dans la génétique des populations, l'équation de Wright décrit l’ascension d’un gradient semblable aux potentiels classiques, mais il n'y a pas d'équivalent de l'énergie cinétique qui permettrait au système de descendre ensuite ce gradient, ce qui serait nécessaire pour la réversibilité du temps.

Références

1. Beatty, J. (1995). « The evolutionary contingency thesis », in Wolters, G. et Lennox, J.  (Eds.), Concepts, theories, and rationality in the biological sciences, Pittsburgh, University of Pittsburgh Press, p. 45-81.
2. Boltzmann, L. 1896. Vorlesungen über Gas Theorie. Leipzig, Germany: Barth.
3. Crow, J. & Kimura, M. 1970. An Introduction to Population genetics Theory. New York, Evanston, and London: Harper & Row, Publishers.
4. Darwin, C. 1859. On the origin of species. London: Murray.
5. Demetrius, L. 2000. Thermodynamics and Evolution. Journal of Theoretical Biology, 206: 1-16.
6. Dollo, L., 1893. Les lois de l’évolution. Bulletin de la Société Belge de Géologie, Paleontology, et Hydrologie, 7: 164-166.
7. Edwards, A. W. F. 1977. Foundations of Mathematical Genetics. Cambridge (UK): Cambridge University Press.
8. Ewens, W. 2012. James F. Crow and the Stochastic Theory of Population Genetics. Genetics, 190, 2: 287-290.
9. Fisher, R. A. 1918. The correlation between relatives on the supposition of Mendelian inheritance. Transactions of the Royal Society of Edinburgh,52: 399-433.
10. Fisher, R. [1930] 1958. The Genetical Theory of Natural Selection. Oxford: Clarendon, 2nd edn 1958. New York: Dover.
11. Fisher, R. A. 1941. Average excess and average effect of a gene substitution. Annals of Eugenics, 11: 53-63.
12. Gayon, J. 1998. Darwinism's Struggle for Survival : Heredity and the Hypothesis of Natural Selection, Cambridge University Press, 1998.
13. Gayon, J. 2014. De la portée des théories biologiques. In: T. Martin, ed., Problèmes théoriques et pratiques en biologie évolutionnaire, Besançon, Presses Universitaires de Franche Comté, p. 13-52
14. Gayon, J., & Montévil, M.. 2017. Repetition and Reversibility in Evolution: Theoretical Population Genetics. Dans C. Bouton & Huneman, P. (Éd.), Time in nature and the nature of time. Springer. p. 275-314.
15. Gould, S. J. 1970. Dollo on Dollo’s Law: Irreversibility and the Status of Evolutionary Laws. Journal of the history of biology, 3, 2: 189-212.
16. Goux, J. M. 1979. Les modèles en génétique des populations. In: P. Delattre & M. Thellier, eds., Élaboration et justification des modèles: applications en biologie, Vol. II. Paris: Maloine, pp. 565-571.
17. Griffiths, Paul E. 1996. The Historical Turn in the Study of Adaptation. The British Journal for the Philosophy of Science, 47, 4: 511-532.
18. Haldane, J. B. S. 1954. The Statics of Evolution. In: J. S. Huxley, A. C. Hardy, and E. B. Ford (eds.). Evolution as a Process. London: Allen and Unwin, p. 109-121.
19. Hardy, G. H. 1908. Mendelian proportions in a mixed population. Science, 28: 49-50.
20. Hartl D. L. 1980 Principles of Population Genetics. Sunderland (MA, Sinauer Associates.
21. Jacquard, A. 1971. Structures génétiques des populations. Paris, Masson. Engl. Trans: The Genetic Structure of Populations, Springer-Verlag, 1974.
22. Kingman, J. F. C. 2000. Origins of the Coalescent: 1974-1982. Genetics, 56: 1461-1463.
23. Kelly, F. P. 2011. Reversibility and Stochastic Networks. Cambridge, Cambridge University Press.
24. Lewontin, R. C. 1967. The Principle of Historicity in Evolution. In: Paul S. Moorehead and Martin Kaplan, eds., Mathematical Challenges to the Neo-Darwinian Interpretation of Evolution. Philadelphia: Wistar Institute Press, pp. 81-94.
25. Li, C. C. 1955. Population Genetics. Chicago: University of Chicago Press.
26. Longo, G. & Montévil, M. 2014. Perspectives on Organisms: Biological time, symmetries and singularities. Coll. ‘Lecture notes in morphogenesis’. Springer
27. Malécot, G. 1948. Les mathématiques de l’hérédité. Paris, Masson.
28. Matthen, M. and Ariew, A. 2009. Selection and Causation. Philosophy of Science, 76: 201-224.
29. Montévil, M. & Mossio, M. 2015. Biological organisation as closure of constraints. Journal of Theoretical Biology, 372: 179-191.
30. Price, G. R. 1972. Fisher’s ’fundamental theorem’ made clear. Annals of Human Genetics, 36, 129-140.
31. Roughgarden, J. 1979. Theory of Population Genetics and Evolutionary Ecology: An Introduction. New York: MacMillan Publishing Co.
32. Simon H. 1977, Models of Discovery. Springer-Verlag.
33. Simpson, G. G., 1964. This View of Life. New York: Harcourt, Brace and World.
34. Sober, E. 1984. The Nature of Selection. Cambridge (MA): MIT Press.
35. Sober, E. 1997. Two Outbreaks of Lawlessness in Recent Philosophy of Biology. Philosophy of Science, 64, Supplement. Biennial Meetings of the Philosophy of Science Association. Part II: Symposia Papers (Dec., 1997), S458-467.
36. Watterson, G. A. 1976. Reversibility and the Age of an Allele. I. Moran’s infinitely Many Neutral Alleles Model. Theoretical Population Biology, 10: 239-253.
37. Watterson, G; A. 1977. Reversibility and the Age of an Allele. II. Two-allele Models, with Selection and Mutation. Theoretical Population Biology, 12: 179-196.
38. Weinberg, N. 1908. Ueber den Nachweis der Vererbung beim Menschen. Jahreshriften des Vereins für Vaterländische Naturkunde in Württemburg, 64: 368-382. Translated in: Papers in Human Genetics, ed. S. H. Boyer (1963), p. 4-15, Englewood Cliffs, NJ: Prentice-Hall.
39. Williams, G. C. 1992. Natural Selection: Domains, Levels and Challenge., New York, Oxford University Press.
40. Wright, S. 1921. Sytems of mating. Genetics, 6: 111-178.
41. Wright, S. 1937. The distribution of gene frequencies in populations. Proceedings of the Natinal Academy of Science, 23: 307-320.
42. Wright, S. 1940. The statistical consequences of Mendelian heredity. In The New Systematics, ed. J. Huxley. Oxford: Clarendon, p. 161–183.