Le sens des formes en biologie
Biomorphisme. Approches sensibles et conceptuelles des formes du vivant
Qu'est qu'une forme en biologie? Au delà des définitions mathématiques, quel est le statut théorique des formes biologiques?
Abstract
Dans l’interface entre biologie et mathématiques, les formes et les processus de morphogenèse sont souvent étudiées pour eux-mêmes. Nous pensons que cette manière de procéder est insuffisante pour capturer le sens biologique de ces formes. La biologie comporte des spécificités qui se manifestent tant sur le plan philosophique que sur celui des principes théoriques : en particulier, tout processus biologique tel qu’un processus de morphogenèse ou une régulation physiologique (i) s’inscrit dans l’évolution et dans une histoire naturelle et (ii) s’intègre dans un organisme dont il dépend et auquel il participe. Nous aborderons alors le sens des formes biologiques à l’aune de ces principes, tant au niveau de la théorie qu’au niveau de la compréhension de l’accès expérimental aux objets biologiques.
Table of contents
Reading time: ~51 min
Le sens des formes en biologie
Résumé
À l’interface entre biologie et mathématiques, les formes et les processus de morphogenèse biologiques sont souvent étudiées pour eux-mêmes. Nous pensons que cette manière de procéder est insuffisante pour saisir le sens biologique de ces formes. La biologie comporte des spécificités qui se manifestent tant sur le plan philosophique que sur celui des principes théoriques : en particulier, tout processus biologique, qu’il s’agisse d’un processus de morphogenèse ou d’une régulation physiologique (i) s’inscrit dans l’évolution et dans une histoire naturelle et (ii) s’intègre dans un organisme dont il dépend et auquel il participe. Nous aborderons alors le sens des formes biologiques à l’aune de ces principes, tant au niveau de la théorie qu’au niveau de la compréhension de l’accès expérimental aux objets biologiques.
1 Comment conceptualiser les formes biologiques ?
Le vivant est caractérisé par la diversité remarquable des formes qu’il donne à voir, qu’il s’agisse des formes du corps des organismes pluricellulaires, de celles de leurs organes et tissus, ou même des formes des cellules et des structures intracellulaires — qu’il s’agisse des cellules d’un organisme pluricellulaire ou d’organismes unicellulaires.
Bien que le concept de forme soit central en biologie, les formes biologiques ne font pas l’objet d’une théorie intégrée. Par exemple, la mathématisation des mécanismes évolutifs, en génétique des populations, contourne la question des formes des formes des phénotypes en postulant directement une relation entre les causes étudiées (génétiques) et ce que sera la génération suivante, ces relations pouvant, bien sûr, comprendre de l’aléatoire ( Gayon 1992). À l’opposé du spectre théorique, l’étude de la morphogenèse, notamment telle qu’elle a été initiée par Turing, considère les formes biologiques comme le résultat d’un processus non-linéaire de nature purement physico-chimique ( Turing 1952).
Dans ce texte, nous allons analyser le concept de forme biologique à l’aune du cadre théorique que nous contribuons à développer ( Soto et al. 2016). Nous insistons sur la dimension théorique et épistémologique de la question car nous pensons que ce n’est qu’une fois enchâssée dans un cadre théorique qu’une notion de forme ou qu’un objet mathématique décrivant des formes peuvent correspondre à un concept rigoureux de forme biologique. Ici, une analogie peut être éclairante. À l’aube de la théorie quantique, les physiciens abordaient les phénomènes avec le concept de trajectoire issu de la mécanique classique, mais les contraintes théoriques et expérimentales les ont conduits à s’en éloigner. Néanmoins, dans certaines expériences effectuées dans les chambres à brouillard, des trajectoires semblaient apparaître. Einstein défendit alors l’idée suivant laquelle « c’est la théorie qui décide ce que l’on peut observer », ce qui est un aspect de ce que l’on appelle aujourd’hui la thèse de Duhem-Quine. Ce qui ressemblait à de trajectoires n’en était donc pas car ce concept n’existe pas en physique quantique — ou, du moins, il n’existe pas du tout de la même manière qu’en mécanique classique ( Heisenberg 2010). De même, nous interrogerons le concept de forme en biologie en partant du principe que, si nous gardons le terme, le concept biologique de forme pourra se détacher de manière très significative des concepts plus habituels de forme, y compris les concepts mathématiques, en fonction des nécessités théoriques propres à l’étude du vivant.
Pour analyser le concept de forme en biologie, il nous semble utile, voire nécessaire, de faire un détour par la physique. En plus de l’intérêt intrinsèque d’une démarche d’épistémologie comparée, cette démarche nous permettra de problématiser l’articulation entre mathématiques et phénomènes biologiques. Elle nous permettra aussi de rendre compte des approches physique des formes biologiques telle que celles effectuées à la suite de Turing. Ce faisant, nous aborderons des enjeux théoriques proprement biologiques qui nous semblent pertinents dans l’optique du biomorphisme.
Dans ce texte, nous allons mobiliser plusieurs concepts de forme. Le premier, et sans doute le plus usuel, est le concept de forme dans l’espace, par exemple comme contour d’un objet — contours qui en biologie sont d’ailleurs souvent matérialisés de manière particulière, par des membranes chez les cellules ou par des cellules particulières, l’épithélium, dans les tissus, y compris la peau. Le second, plus abstrait mais néanmoins dans la continuité du premier car il en est une généralisation, concerne les formes mathématiques que l’on mobilise pour comprendre les phénomènes. Comme nous allons l’exposer, la compréhension mathématique des phénomènes, en particulier en physique, fait intervenir des formes dans des espaces plus généraux que l’espace tridimensionnel usuel, comprenant donc, par exemple, l’espace, la vitesse, le temps, etc., ce qui permet, par exemple, de parler de la forme d’une trajectoire. Ces formes correspondent aussi à l’écriture formelle, équationnelle typiquement, utilisées pour les décrire et plus généralement pour les théoriser. Dans ce texte, nous analysons les formes à ces deux niveaux, d’autant que nous posons que l’analyse des formes dans l’espace n’a de sens qu’en lien avec leur rôle théorique, rôle qui est typiquement explicité à l’aide du second concept, plus large. Dans le cadre de la biologie, nous allons cependant mettre ces concepts en tension afin de saisir le sens des formes du vivant.
2 Formes et raisonnement en physique
Avant de nous pencher sur la biologie, nous allons aborder succinctement comment la physique articule mathématiques et phénomènes naturels en nous penchant, après des considérations générales, sur la question de la morphogenèse.
En mécanique classique, un système est défini par la structure des relations entre ses parties et cette structure ne change pas dans la dynamique du système. Par exemple, deux planètes s’attirent mutuellement suivant la loi de la gravitation universelle décrite par Newton, ce qui permet de comprendre la forme des trajectoires — des ellipses lorsque l’on considère que le problème est limité à deux corps.
Examinons maintenant les « ingrédients » intervenant dans la définition d’un tel système ( Montévil 2018).
- L’état d’un système le représente par sa position dans l’espace des possibles qui est considéré comme donné à l’avance. L’état du système change au cours du temps et, réciproquement, les changements du système sont des changements d’état, donc de position dans cet espace. Par exemple, en mécanique classique, l’état du système est la position et la vitesse de ses différents constituants tels que la Terre et le Soleil.
- Les paramètres sont des quantités nécessaires à la description du système mais ne changeant pas dans sa dynamique. La masse des objets ou leur charge électrique sont typiquement des paramètres en mécanique classique.
- Enfin, et c’est le plus important, le système est décrit par des règles, et, plus précisément, dans le cas de la mécanique classique, des règles déterminant les changements d’état lorsque le temps s’écoule. Ces règles sont écrites sous forme d’équations telle que le principe fondamental de la dynamique : la masse fois l’accélération est égale à la somme des forces extérieures. L’accélération étant le taux de changement de vitesse, et la vitesse le taux de changement de position, cette équation donne bien une règle pour les changements d’état.
Ces règles écrites sous forme d’équation ne sont pas a priori— elles ne sont pas indépendantes de l’expérience —, mais elles ne sont pas pour autant arbitraires. Comment sont construits et justifiés de tels cadres théoriques ?
Dans ces cadres théoriques, ce ne sont pas tant les quantités en tant que telles qui comptent mais les relationsentre quantités. Par exemple, 1 kg d’or ou 1 kg de plomb pèsent tous les deux 1 kg parce que les forces exercées par le champ de pesanteur sur ces deux objets sont égales. Ceci est bien représenté par les balances anciennes, à plateau, dont le dispositif vise précisément à comparer les forces exercées par le champ de pesanteur sur deux objets et donc à les rendre commensurables. Cet exemple ne décrit qu’une simple relation de proportions : dans le cas du champ de pesanteur, la force est proportionnelleà la masse de l’objet. Plus généralement, c’est bien la formedes relations entre quantités qui est l’enjeu théorique majeur et qui vient structurer et justifier les équations utilisées.
Pour aller plus loin, il faut introduire un concept clé de la physique théorique et qui n’est pas non plus sans application en biologie : le concept de symétrie. En deux mots, une symétrie est une transformation qui ne change pas les propriétés pertinentes d’un objet. Par exemple, une sphère est symétrique par rotation. Un autre exemple, plus fondamental, est le principe de relativité qui stipule qu’il n’y a pas de système de référence absolu — il n’y a pas de centre dans l’univers, ni de point fixe —, mais que les équations fondamentales de la physique doivent avoir la même forme quel que soit le système de référence. Les changements de systèmes de références acceptables dépendent bien sûr de la théorie et constitue les symétries de l’espace-temps de cette théorie (relativité galiléenne, relativité restreinte, relativité générale, et d’autres exemples ne concernant plus l’espace-temps stricto sensuseraient tout aussi pertinents).
Ces exemples montrent que le concept de symétrie est omniprésent pour structurer les équations décrivant des phénomènes physiques ( Van Fraassen 1989; Bailly et Longo 2006). Ils montrent aussi que son utilisation peut avoir des statuts divers : la symétrie de la sphère est propre à un objet particulier et sans doute une approximation du réel, alors que les symétries de l’espace-temps sont principielles dans les théories concernées. Le concept de symétrie intervient aussi de manière mathématiquement plus complexe mais non moins importante théoriquement et épistémologiquement. Par exemple, le théorème de Noether interprète les quantités conservées en physique, telles que l’énergie, comme une conséquence de symétries sous-jacentes ( Byers 1999). Dans le cas de l’énergie, il s’agit de la symétrie par translation dans le temps c’est-à-dire, informellement, l’hypothèse que l’avancée du temps ne change pas l’équation d’un système isolé.
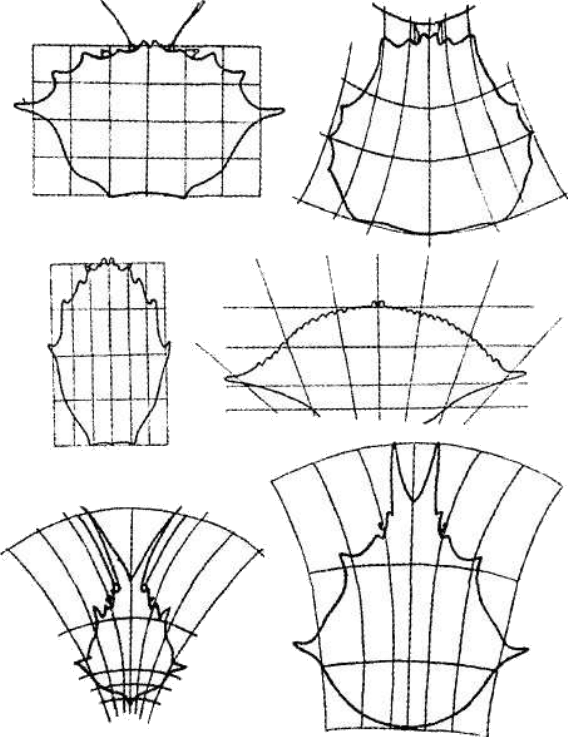
Comme nous l’avons suggéré, le concept de symétrie est aussi utilisé en biologie. Il est pertinent par exemple pour décrire la forme globale des corps, tel que dans le cas de la symétrie bilatérale. Ce concept intervient aussi de manière plus abstraite, c’est à dire en un sens plus proche de celui de la physique théorique. Par exemple, D’Arcy Thompson interprète une partie de la diversité des formes biologiques comme issue de déformations. Derrière la diversité des formes biologiques se trouverait ultimement une unité plus fondamentale ( Thompson 1942). Dans cette analyse, ce n’est pas tant une forme donnée qui est pertinente mais ce sont les déformations et leur nature, voir figure 2 . Toutes les formes d’une classe d’organismes sont alors comprises comme déformations de l’une à l’autre, bref comme étant symétriques et préservant certaines propriétés de la forme originelle. Bien sûr, dans cette approche, le problème reste de savoir comment la forme originelle est apparue, nous y reviendrons.
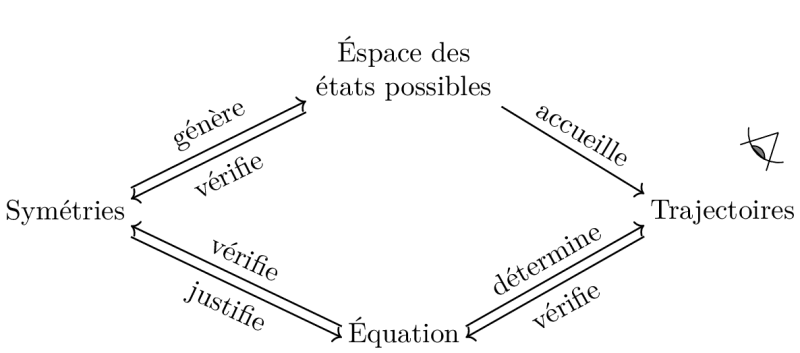
Avant d’aborder les modèles physiques de morphogenèse, concluons sur le type d’objet que cette méthode d’appréhension du réel conduit à décrire. La physique repose sur un cercle vertueux, voir figure 3 . Les changements d’un objet sont alors compris comme des déplacements dans un espace mathématique pré-donné. Ces changements constituent alors des trajectoires qui sont déterminées théoriquement par des équations — certes parfois de manière probabiliste — et les variables de ces équations constituent l’état de l’objet (complétées par des paramètres fixés par l’extérieur du système). Derrière les équations et la structure de l’espace des états possibles se trouve plus profondément des structures mathématiques de symétrie pouvant être analysé et discuter théoriquement (l’invariance des « lois » physiques au cours du temps est beaucoup plus intuitive que la conservation de l’énergie, la définition de l’énergie étant en elle-même assez abstraite). L’ensemble de cette structure théorique permet de se confronter à l’expérience en mesurant les trajectoires d’objets réels, c’est-à-dire en mesurant les quantités décrivant les états.
Ce cercle épistémologique vertueux a néanmoins un prérequis que l’on peut aussi voir comme une conséquence. Dès lors qu’il est appliqué à des phénomènes, alors la compréhension de ces phénomènes semble bien pouvoir se détacher de leur matérialité : la compréhension peut procéder sur la base de la structure de la détermination théorique décrite par les mathématiques. Ainsi, l’effet de la gravitation sur une pomme et sur une planète est le même car il est décrit par les mêmes équations, le même espace des possibles, les mêmes paramètres et les mêmes trajectoires. Il faut bien comprendre ici que ce cercle vertueux ne peut pas s’appliquer à un seul objet concret, et encore moins à un seul objet à un seul instant. En effet, les équations décrivent des relations génériques entre les états et les changements d’états, ces relations s’appliquent tout au long de la trajectoire, et les symétries décrivent des transformations, donc nécessairement une pluralité de situations de manière conjointe et simultanée. Le type de compréhension obtenue va donc être la compréhension d’une collectivité de situations concrètes subsumées par un seul objet théorique et mathématique, ce que nous appelons la généricité de l’objet théorique en physique à la suite de Bailly et Longo ( 2006), Montévil, Mossio et al. ( 2016) et Montévil ( 2019b). Le rôle de l’écriture (mathématique) est ici central. Dès lors que l’on est en mesure d’écrire de manière mathématique la détermination théorique de l’objet, ce qu’il y a à savoir sur cet objet pourra être obtenu par la poursuite de cette écriture sous forme de preuves mathématiques : la compréhension du phénomène a été détachée de l’objet concret.
Ce contexte épistémologique et théorique est nécessaire pour comprendre la nature des modèles de morphogenèse en physique. Discutons quelques cadres assez généraux de compréhension de la morphogenèse. Le premier est celui des brisures de symétrie. Prenons un exemple de la vie quotidienne : imaginons un crayon placé sur une table parfaitement à la verticale sur sa mine. La situation initiale est parfaitement symétrique par rotation : en prenant comme centre le crayon, toutes les directions sont équivalentes. Cette configuration est instable, une fluctuation de l’air environnant ou une légère imperfection dans la position du crayon vont le conduire à tomber. Une direction a lors été singularisée : la direction dans laquelle le crayon est tombé. La symétrie initiale est donc brisée. La situation initiale étant parfaitement symétrique par rotation et toutes les directions étant donc initialement équivalentes, la situation initiale ne permet pas de spécifier la direction dans laquelle tombera le crayon. La brisure de symétrie implique donc le concept d’aléatoire, et de manière consubstantielle l’introduction d’une nouveauté dans le système : la direction dans laquelle le crayon est tombé, donc la manière dont la symétrie a été brisée. Le fait que ce raisonnement permette de comprendre l’apparition d’une nouveauté le rend particulièrement adapté pour comprendre la genèse d’une forme et Turing ( 1952) l’utilise. Il est utilisé dans de nombreux contextes théoriques et mathématiques comme les changements d’état de la matière, notamment la cristallisation, ou même l’apparition des forces fondamentales dans la théorie quantique des champs ( Longo et Montévil 2014; Strocchi 2005).
Dans ces modèles de morphogenèse, la même équation fondamentale reste vérifiée. Néanmoins les solutions auxquelles elle conduit peuvent enfreindre une symétrie initiale du problème. Il s’agit d’une infraction au principe de Curie suivant lequel la symétrie des causes se retrouve dans les effets. Notons bien que, ici, ce n’est qu’une seule symétrie qui est enfreinte parmi les multiples symétries impliquées dans la définition théorique et mathématique des objets. En un mot, dans ces situations, la trajectoire a quelque chose de plus que les équations (la direction dans laquelle la symétrie est brisée), mais cet élément supplémentaire est rendu nécessaire par les équations, et sa nature est pré-donnée par les équations. Briser une symétrie suppose que cette symétrie soit décrite avant qu’elle ne soit brisée. La situation est similaire dans la théorie des catastrophes de René Thom ( Thom 1974) même si le concept de symétrie y est moins central. Dans ce dernier contexte théorique, une équation peut conduire à des trajectoires ayant des propriétés qualitatives distinctes et l’on peut passer de l’une à l’autre par une catastrophe. Toutefois, dans ces analyses et dans d’autres analyses en physique, il s’agit toujours de revenir un petit nombre de cas génériques, à un niveau de description ou à un autre ( Montévil 2019b).
Pour conclure cette section, abordons le modèle proposé par Douady et Couder afin de comprendre certains patrons apparaissant dans la croissance des plantes ( Douady et Couder 1996). Il n’est pas utile ici d’aborder la formulation du modèle lui-même, mais la démarche utilisée mérite d’être discutée. Une partie de l’argumentation des auteurs réside dans le fait que ce modèle peut être instancié par un objet expérimental entièrement abiotique, et qu’en faisant cette expérience les mêmes patrons n’apparaissent que chez les vivants concernés. Comme nous l’avons discuté, cette démarche est parfaitement cohérente avec le processus d’objectivation développé par la physique : par construction l’intelligibilité physico-mathématique se détache des objets particuliers. Cet exemple montre aussi qu’il n’y a rien de spécifiquement biologique dans ces modèles de morphogenèse. Il y a alors deux possibilités. Soit la morphogenèse et plus généralement les formes des objets biologiques n’ont effectivement rien de distinct par rapport aux morphogenèses et formes physiques. Soit, au contraire, les spécificités biologiques disparaissent dans la modélisation physique à cause de la méthode de modélisation elle-même, et il faut envisager un cadre différent pour comprendre les formes biologiques de manière théoriquement précise. Nous argumentons dans la seconde direction dans la section suivante. Notons que le problème s’étend, mutadis mutandis, aux formes comprises dans le sens le plus large, tel que la forme des processus.
3 Les formes biologiques
Pour comprendre le rôle des formes en biologie, nous allons inscrire ce concept dans un cadre théorique plus large. Il s’agira de cerner comment les formes interviennent dans la compréhension du vivant et surtout quel concept de forme peut être articulé à ce cadre théorique.
3.1 Historicité et définition théorique des objets biologiques
En physique, nous l’avons vu, certaines régularités (mathématiques) sont assimilées à des « lois » ou, de manière plus moderne, constituent des principes théoriques. En biologie, au contraire, les régularités varient au cours du développement et de l’évolution. Par exemple, la génétique des populations est parfois comparée à la mécanique classique dans sa version déterministe et la mécanique statistique dans sa version probabiliste. Pourtant la transmission des gènes se fait de manière fort diverse et surtout est historiquement située. Elle peut être, par exemple, haploïde, diploïde voire décaploïde, mais il existe aussi d’autres variantes telle que des combinaisons entre reproduction par parthénogenèse et sexuée, ou la polyembryonie monozygotique, c’est-à-dire le fait de donner naissance à quatre clones dans le cadre d’une reproduction sexuée, rencontré chez le mammifère Dasypus novemcinctus(le tatou à neuf bandes). Toutes ces variations sont apparues dans l’évolution, c’est-à-dire l’histoire du vivant, et changent les équations de la génétique des populations. Ces dernières ne peuvent alors plus être considérées de manière anhistorique.
Dans ce contexte, les régularités biologiques mobilisables pour écrire des équations, notamment les symétries, ne peuvent plus être appréhendées comme principielles, elles sont elle-même l’objet de changements. L’invariance ne permet alors plus de comprendre les changements. Nous suivons l’idée qui consiste à réinterpréter ces régularités comme des contraintes plutôt que comme des “lois” ( Montévil et Mossio 2015; Soto et al. 2016; Montévil, Mossio et al. 2016). Cette perspective est cohérente avec la thèse de la contingence de Beatty ( 1995), suivant laquelle toute loi proprement biologique est historiquement contingente. Les contraintes sont alors des régularités mais des régularités fondamentalement contingentes contrairement aux régularités principielles en physique. Dans la compréhension du terme de contrainte, il ne faut pas se cantonner à l’idée intuitive suivant laquelle les contraintes empêchent certaines choses de se produire. En même temps que les contraintes limitent ce qui peut se passer, elles rendent possible d’autres choses. Une bonne analogie est celle du jeu : les règles d’un jeu limitent les actions possibles mais, par ces limitations, elles rendent le jeu possible et intéressant — elles n’en restent pas moins contingentes et peuvent être enfreintes ou changée.
Les contraintes sont susceptibles de changer et leur stabilité, le cas échéant, demande à être expliquée. Il y a au moins deux types d’explications de la permanence de certaines régularités. La première est la sélection naturelle, qui est d’abord un principe de conservation comme le souligne Guillaume Lecointre ( Lecointre 2017) et le suggère le sous-titre de l’ Origine des espèces, “the preservationof favoured races in the struggle for life” ( Darwin 1859, nous soulignons) — la variation étant en amont. Le deuxième principe expliquant la relative stabilité des contraintes biologiques, que nous détaillerons ci-dessous, est le maintien mutuel des contraintes d’un organisme et donc leur interdépendance — cette interdépendance conduit à ce que les parties d’un organisme se dégradent rapidement à la mort de celui-ci, lorsque son organisation se disloque.
En biologie, les changements de contraintes brisent le cercle vertueux représenté en figure 3 dans le cas de la physique. Un changement de contrainte s’accompagne d’un changement d’équation et d’un changement d’espace des états possibles, de sorte que la trajectoire de l’objet ne vit plus dans le même espace. Ni l’équation, ni l’espace de description ne peuvent donc rendre compte de tels changements. Autrement dit, le changement ne plus être compris sur la base de l’invariance, ni être compris comme déplacement dans un espace pré-donné. L’espace des possibles comme les équations doivent alors être conçus comme étant générés par les changements du vivant.
Dans un tel contexte, le cercle vertueux en physique, illustré par la figure 3 , est brisé, et est donc brisée aussi la justification de la théorisation et de la modélisation mathématique telle que cette dernière est pratiquée en physique, avec ses symétries et quantités conservées principielles. Alors, il n’y a plus de justification théorique, ni de méthode pratique, pour considérer l’objet biologique comme un objet générique. On ne peut pas parler d’un chat comme on peut parler d’un électron. Un électron se comporte comme tous les électrons alors qu’un chat peut être un Maine coon ou un chat persan, et, de la même manière, deux chats Maine coon auront des différences. Les individus biologiques sont tous significativement différents comme le notait déjà L’Héritier ( 1949). Ici, nous retrouvons aussi l’idée développée par Canguilhem ( 1972) suivant laquelle l’homme moyen n’existe pas — et le chat moyen non plus, nous y reviendrons.
Autrement dit, l’objet biologique ne peut plus être objectivé par des relations causales stables entre ses parties. Les contraintes ne définissent pas les objets, elles en sont une propriété à un moment donné. Les objets biologiques sont alors issus d’une cascade de changements de leurs contraintes, et ils sont donc d’abord définis par l’histoire dont ils proviennent, étant entendu qu’ils continuent à produire une histoire par des changements de contraintes. Insistons ici, les changements de contraintes ne sont pas des déplacements dans un espace des possibles pré-donné, leur nature théorique est donc tout à fait originale par rapport à la physique. Les objets biologiques deviennent alors des objets spécifiques par opposition avec les objets génériques de la physique ( Montévil, Mossio et al. 2016), voir figure 4 . Pour ces raisons, Giuseppe Longo oppose le temps des processus, c’est-à-dire le temps des changements d’état, et le temps historique, celui du changement des contraintes ( Longo 2018). Stuart Kauffman parle, lui, de la fin de la vision physicaliste du monde à cause de la croissance des possibles au cours du temps (Stuart A Kauffman 2019). Cette perspective rejoint aussi celle du paléontologue Gould et notamment sa critique de l’approche de D’Arcy Thompson au profit de la centralité de la contingence historique en biologie ( Gould 2002, chap.10 ; Stiegler 2015).
Dans ce cadre, les objets biologiques deviennent aussi contextuels en un sens fort : la présence de telle ou telle contrainte peut dépendre du contexte. Plus encore, l’historicité et la contextualité se couplent car les contextes passés ont été intériorisés par les organisations biologiques ( Miquel et Hwang 2016).
Il manque un cadre théorique et mathématique pour comprendre les changements de contraintes et, en particulier, le type de causalité propre à ce cadre théorique qui a été appelée « enablement», c’est-à-dire rendre possible ( Longo, Montévil et S. Kauffman 2012). En effet, l’apparition d’une nouvelle contrainte ne peut être déduite de contraintes préexistantes, mais certaines contraintes préexistantes sont néanmoins nécessaires à cette apparition. Par exemple, les mâchoires articulées sont nécessaires à l’apparition des dents ; rétrospectivement, elles ont contribué à les rendre possibles.
Il ne s’agit pas, pour nous, de proposer seulement une réinterprétation des régularités biologiques qui viendrait limiter la portée des travaux de modélisation. Ce cadre épistémologique et théorique vise aussi, et l’on pourrait même dire surtout, à transformer les méthodes de compréhension du vivant, et notamment les méthodes de modélisation, pour les rendre plus adéquate aux phénoménalités biologiques.
Donnons un exemple de méthode que nous sommes en train de développer. Cette méthode s’inspire librement du concept philosophique de déconstruction de Jacques Derrida, qui s’applique aux concepts dans leur historicité et que nous visons à déployer sur des modèles mathématisés. L’idée est de considérer un modèle ou une structure mathématique biologiquement pertinente et de la déconstruire, hypothèse par hypothèse, en regardant à chaque étape quel sens biologique peut avoir la négation de l’hypothèse considérée. Plus précisément, les régularités permettant de définir un modèle mathématique sont des contraintes. En tant que telle, elles peuvent changer, ce qui a été appelé principe de variation ( Montévil, Mossio et al. 2016), et en déconstruisant l’objet mathématique nous explorons certaines de ces variations — celles qui ne demandent pas d’hypothèses supplémentaires.
Nous pouvons donner un exemple simple de l’approche de déconstruction d’une structure mathématique biologiquement pertinente, et plus précisément d’une forme mathématique utilisée pour décrire des formes anatomiques. La structure épithéliale des glandes mammaires de rat est généralement décrite mathématiquement comme un arbre (axiomatisé mathématiquement comme un graphe acyclique et connexe). La négation des hypothèses construisant mathématiquement la structure d’arbre conduit à :
| Hypothèse | Négation |
| Acyclique | Présence de boucle (en rouge) |
| Connexe | Présence de partie détachée de l’arbre principal (en bleu) |
| Composé de nœuds et d’arêtes (graphe) | Présence de connections ambiguës (jonction des épithéliums mais pas des lumières) |
| Composé de nœuds et d’arêtes (graphe) | Pas d’arête définie (tumeur) |
À la suite d’un travail sur le rat, en utilisant une seule expérience, nous avons des preuves empiriques de la pertinence biologique de chaque prédiction de la déconstruction, à l’exception toutefois de la dernière, les tumeurs, dont l’existence est bien connue par ailleurs. Deux de ces prédictions sont illustrées en figure 5 . Dans chaque cas, les « anomalies » ont des conséquences pour l’utilisation de la structure d’arbre afin de représenter l’objet biologique. Il ne s’agit pas ici de se contenter de dire que l’objet biologique est plus complexe que sa représentation mathématique, mais bien de dire que les variations biologiques peuvent sortir des cadres mathématiques utilisés pour les représenter, et ceci pour des raisons principielles, ce qui n’est pas qu’un résultat négatif mais au contraire permet certaines prédictions.
Le concept de forme qui se dégage de cette discussion est un concept qui ne possède pas d’invariance principielle. Une forme mathématique donnée n’est pas nécessairement préservée dans une espèce, elle est associée à d’autres possibles donnés, par exemple, par la déconstruction de cette forme. Le concept de forme biologique qui nous semble biologiquement pertinent, et que nous associons ici à celui de contrainte, n’est donc jamais un invariant stricto sensumais est un invariant historicisé, de telle sorte qu’une forme mathématique donnée en biologie emporte avec elle d’autres formes mathématiques et ceci pour des raisons principielles.
3.2 L’intégration des formes dans l’organisme
Si l’on pose la variation comme première, nous l’avons mentionné, la stabilité relative des contraintes demande à être expliquée puisque nous ne pouvons plus la postuler comme nous postulons les “lois” en physique. Un type d’explication que nous avons évoqué est l’interdépendance entre les parties d’un organisme.
La question du rapport entre partie et tout est principielle en physiologie. Ainsi, Bernard ( 1865) affirme que :
Le physiologiste et le médecin ne doivent donc jamais oublier que l’être vivant forme un organisme et une individualité. [...] Il faut donc bien savoir que, si l’on décompose l’organisme vivant en isolant ses diverses parties, ce n’est que pour la facilité de l’analyse expérimentale, et non point pour les concevoir séparément. En effet, quand on veut donner à une propriété physiologique sa valeur et sa véritable signification, il faut toujours la rapporter à l’ensemble et ne tirer de conclusion définitive que relativement à ses effets dans cet ensemble.
(Bernard 1865, p.154)
En plus de son inscription historique et contextuelle, un modèle physique instanciable par un objet abiotique comme dans le travail de Douady et Couder ( 1996) manquera donc son inscription dans l’organisme. La question de cette inscription a été l’objet de nombreux travaux en biologie théorique. Mentionnons quelques exemples. Le concept d’autopoïèse de Varela, Maturana et Uribe ( 1974) pose que les constituants d’un organisme sont produits par cet organisme. Le concept d’ensemble autocatalytique de Stuart A. Kauffman ( 1993) pose, lui, qu’une étape cruciale dans l’apparition de la vie est l’apparition d’un ensemble de molécules capables de catalyser la production des molécules de cet ensemble, de sorte que ces molécules sont collectivement autocatalytiques. Enfin, Rosen ( 1991) propose une approche plus abstraite de ces questions, sur la base de la théorie des catégories, où la circularité entre le métabolisme et la réparation des constituants d’un objet est au centre de l’analyse. Ces concepts sont l’objet d’un certain nombre de travaux (J. C. Letelier, Marin et Mpodozis 2003; Ruiz-Mirazo et Moreno 2004;J.-C. Letelier, Cárdenas et Cornish-Bowden 2011), mais s’ils sont très pertinents pour la question de l’origine de la vie, ils peinent à s’articuler avec les travaux biologiques plus quotidiens, qu’il s’agisse de travaux expérimentaux ou de modélisations.
Un nouveau cadre satisfaisant plusieurs objectifs et limites des cadres précédents a été publié récemment. Ce cadre visait tout d’abord à dépasser les définitions purement chimiques de la matière, conduisant à l’idée qu’être autopoïètique signifie seulement produire les molécules constituant un organisme. En effet, les êtres vivants produisent et maintiennent aussi des formes telles que celle du système vasculaire et de la membrane d’une cellule, ou, de manière plus abstraite, la cyclicité cardiaque. Pour cela, le concept de contrainte a été utilisé pour généraliser ces idées à toutes sortes de régularités et donc de formes. Un autre objectif de ce travail était de distinguer à quel niveau et pour quel type d’objet se présente la circularité que tous les travaux susmentionnés en biologie théorique visent à saisir. Il faut ici avoir présent à l’esprit que les êtres vivants sont, pour des raisons principielles, thermodynamiquement ouverts. En effet, comme le souligne Schrödinger ( 1944), les êtres vivants ne sont pas au maximum d’entropie et, d’après le second principe de la thermodynamique, pour ce maintenir ainsi ils doivent être traversés par des flux d’énergie et de matière. En distinguant processus de transformation et contraintes, ces circularités peuvent être décrites comme clôture entre contraintes, c’est-à-dire l’idée qu’une contrainte structure un processus de transformation maintenant une autre contrainte qui agit sur un autre processus, et ainsi de suite jusqu’à ce que la première contrainte soit maintenue ( Montévil et Mossio 2015). Enfin, un objectif dans la formulation de ce cadre était de le rendre compatible avec la variation biologique telle que décrite ci-dessus. Ainsi, les contraintes ne sont valide qu’à une échelle de temps donnée, et le rôle épistémologique de cette circularité est transformé : il ne s’agit plus tant de savoir ce qui distingue le vivant du physique ou même de savoir comment l’apparition du vivant a été possible (ou aussi possiblement nécessaire) mais de comprendre pourquoi et comment certaines parties des organismes se maintiennent dans le temps. Plusieurs exemples d’application à des situations biologiques précises ont été développé ( Montévil, Speroni et al. 2016; Bich, Mossio et Soto 2020).
Dans ce cadre, les contraintes participant à la clôture interviennent de deux manières distinctes. D’une part, une contrainte faisant partie de la clôture est maintenue par un processus sous l’action d’une autre contrainte de l’organisation. D’autre part, elle agit sur au moins un autre processus maintenant une autre contrainte de l’organisation. Par exemple, la géométrie du système vasculaire est maintenue par le renouvellement de ses cellules et les processus de cicatrisation, et il contraint le flot d’oxygène et de nombreux autres composés dans l’organisme, ce qui, en deux mots, maintient les propriétés du milieu intérieur. Nous voyons donc ici qu’une forme biologiquement pertinente n’est jamais pertinente par elle-même. Elle est pertinente par son inscription dans une organisation, donc dans une circularité qui implique ce double statut comme objet d’un maintien et participation au maintien d’au moins une autre partie.
Il est important de noter que la circularité propre à la clôture entre contraintes et aux approches similaires est un moyen d’interpréter la notion de fonction biologique ( Mossio, Saborido et Moreno 2009). Une contrainte a une fonction lorsqu’elle fait partie de la clôture, car son existence dépend de ses conséquences par la circularité de la clôture. L’autre approche philosophique du concept de fonction est le concept sélectionniste qui pose qu’un trait a une fonction s’il a été sélectionné à cause de ses effets ( Godfrey-Smith 1994). Il est intéressant de noter que ces deux approches correspondent à deux manières d’expliquer la relative stabilité d’une contrainte dans le cadre que nous mobilisons.
Dans ce cadre, les formes biologiques ne sont donc pas simplement des formes mathématiques. Lorsqu’elles font partie de l’organisation d’un organisme, elles ont un double statut. Elles sont à la fois l’objet d’un maintien actif par un processus sous contrainte et elles agissent sur un processus stabilisant une autre contrainte, dans une organisation caractérisée par sa circularité. Ainsi, les concepts de formes et de fonctions sont articulés étroitement.
3.3 Que veut dire mesurer des formes biologiques ?
Avant de conclure, abordons une question théorique majeure : le sens théorique de l’accès à l’objet empirique. En physique théorique, le concept correspondant est celui de mesure et il est défini avec précision dans les principales théories physiques. En physique classique, le concept de mesure pose que l’accès à l’état d’un objet n’est jamais parfait, mais qu’il est au contraire toujours approché : alors que l’état est un point, la mesure fournit un intervalle. En physique quantique, la mesure est plus complexe car elle change l’objet de manière irréversible et c’est dans ce contexte qu’Einstein a énoncé l’idée suivant laquelle c’est la théorie qui dit ce que l’on peut observer.
En biologie, cette question a relativement peu été discutée et la mesure biologique n’a pas été formalisée. Montévil ( 2019a) vise à commencer à combler ce manque, (voir aussi
Houle et al. 2011, pour une perspective complémentaire). Pour aborder ce problème, nous pouvons partir du cadre présenté en figure 4 . Dans ce cadre, mesurer un objet biologique ne signifie pas seulement mesurer une partie ou un aspect intéressant dans le cadre d’un travail, comme la masse d’un organisme, la concentration d’une espèce chimique ou la longueur d’un os. Il est aussi nécessaire de “mesurer” l’organisme lui-même et donc l’objet biologique en tant qu’il est spécifique. Par exemple, le poids d’une souris ou son rythme cardiaque n’ont pas le même sens que ceux d’un rat ou d’un éléphant, ils ne sont pas commensurables en tant que tels. Pour les rendre commensurables, nous avons besoin d’un cadre tout à fait distinct de ceux rencontrés en physique.
Les biologistes décrivent et manipulent les objets biologiques en prenant comme référence non pas l’objet tel qu’il est (un état) ou même tel qu’il se comporte (équations) mais en se référant au passé de cet objet. Ainsi, les groupes définis par la classification du vivant doivent désigner uniquement et tous les descendants d’un ancêtre commun. Définir les objets ainsi, à partir d’un point de référence dans le passé, permet d’obtenir des définitions stables quelles que soient les variations des objets biologiques. Les objets biologiques génèrent de la diversité de telle sorte que l’invariance ne permet pas de les définir rigoureusement. Au lieu de propriétés conservés, le passé de l’objet sert de référence. Ici, la généalogie, concept issu de la théorie de l’évolution, joue un rôle central. Bien évidemment, la proximité généalogique va avec la présence simultanée de nombreux caractères, mais la conservation d’aucun de ces caractères et encore moins de leurs fonctions n’est garantie en principe, ni nécessaire, pour que les définitions restent valides.
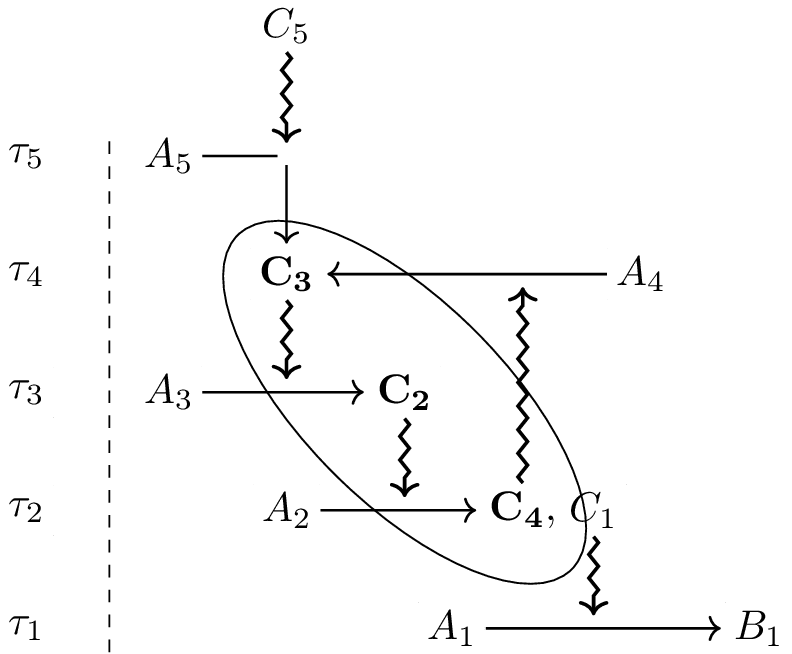
Ce rôle du raisonnement historique n’est pas limité à la classification du vivant en systématique. Les biologistes travaillent souvent avec des souches d’animaux et de cellules de laboratoire, issus de généalogies contrôlées. Ici aussi, l’appartenance à une souche provient de l’existence d’un ancêtre commun qui peut être plus ou moins récent suivant la souche utilisée et sa définition. En figure 7 , nous présentons le cas de cellules et la définition d’une souche (ou d’une sous-souche) provenant d’une seule cellule, leur dernier ancêtre commun. Cependant, même dans ces conditions, la variation ne cesse pas et il est possible d’observer l’évolution dans des conditions de laboratoire ( Papadopoulos et al. 1999).
La mesure biologique implique donc la référence au passé et non seulement à l’objet tel qu’il peut être défini par des relations invariantes. Cette notion de mesure signifie que l’on ne peut pas instancier de novoun objet biologique. Pour reproduire une expérience biologique, il faut travailler sur des objets ayant un passé commun. Cette situation est tout à fait différente de la situation en physique où l’on peut mesurer la vitesse de la lumière dans le vide avec n’importe quel photon, généré de manière complètement indépendante, car ils suivent tous, par principe, les mêmes équations. L’articulation entre connaissance et matière est différente en biologie : la référence au passé passe par la référence à un objet matériel particulier, à un “ceci”, alors que cette approche n’est pas nécessaire en physique.
Les objets biologiques ne sont jamais rigoureusement assimilables l’un à l’autre, l’avancée du temps produit sans cesse des variations, ce qui conduit à définir sans cesse de nouvelles souches et sous-souches d’animaux. L’acte qui consiste à considérer que des objets biologiques sont équivalents dans le cadre d’un travail empirique est un acte de symétrisation. La symétrisation inclut parfois aussi des actions tout à fait concrètes, comme le fait de mettre des organismes dans un même contexte. La symétrisation peut être effectuée de plusieurs manières. Elle peut viser à obtenir des objets dont les organisations sont aussi proches que possibles en prenant des objets dont l’histoire commune est aussi récente que possible, comme en figure 7 ou en étudiant une souche très précise de souris. À l’opposé, la symétrisation peut laisser plus de place à la diversité du vivant, par exemple en étudiant plusieurs souches de souris ou des souris sauvages, ce qui conduit à une plus grande variabilité des résultats mais permet aussi de s’extraire de comportements qui sont propres à une souche de souris particulière, bref d’obtenir des résultats ayant une certaine généralité. Dans ce cadre théorique, le contexte est aussi un élément clé, y compris les contextes passés, et leurs contrôles participent à cette démarche de symétrisation ( Montévil 2019a).
Dans ce cadre, mesurer une forme biologique ne signifie donc pas simplement mesurer une forme mathématique. Pour mesurer une forme biologique, il est nécessaire de se référer aussi à l’histoire et au contexte de l’objet sans quoi une forme mathématique qui peut être observée n’a pas de sens biologique empirique et théorique.
4 Conclusion
Du point de vue de la théorie, les formes biologiques ont alors un statut tout à fait particulier, éloignée des concepts et de l’épistémologie de la physique. En biologie, l’objet ne peut plus être reconstruit théoriquement sur la base de symétries et d’invariants. Il s’ensuit que les formes ne peuvent plus être conçues comme des propriétés invariantes des objets, elles sont des contraintes dont la validité a fondamentalement un caractère contingent.
Les formes biologiques s’inscrivent alors dans une histoire biologique ce qui a plusieurs conséquences. Tout d’abord, l’organisme dont une partie ou un aspect possède cette forme doit aussi être spécifié, et cette spécification, pour des raisons pratiques et théoriques, se fait par la référence au passé de cet organisme, passé qu’il a en partage avec d’autres organismes pouvant faire l’objet d’une même expérience. De plus, même pour des animaux ou des cellules de laboratoire dont l’origine et le contexte sont fortement contrôlés, la présence d’une forme s’accompagne, en droit, de la présence de nombreuses variations de cette forme. Nous avons montré qu’il est possible de tirer parti de cette situation en esquissant une méthode de déconstruction des formes. En quelque sorte, la biologie demande donc de désessentialiser la forme des formes.
Les formes biologiques font, de plus, partie d’objets organisés. Il s’ensuit qu’elles ont un double statut, celui d’être maintenu activement par un processus sous contrainte et celui de maintenir une autre contrainte en contraignant un processus. Le sens d’une forme biologique réside d’abord dans ces articulations avec l’organisation à laquelle elle participe. L’intégration à une organisation permet de comprendre la relative stabilité des formes biologiques comme le résultat d’une activité constante.
La circularité propre à l’organisation comme clôture entre contrainte, mais aussi la contingence fondamentale des contraintes composant ces organisations, et donc leur capacité à varier, sont caractéristiques de l’autonomie des êtres vivants dont les formes sont une manifestation remarquable. Cette autonomie n’est en rien une indépendance, bien au contraire, les organisations biologiques sont contextuelles et plus encore elles portent en elle les traces de leurs couplages avec leurs contextes passés. Détacher les formes de cet ancrage revient à les détacher de leur sens biologique.
Références
- Bailly, F. et G. Longo (2006). Mathématiques & sciences de la nature : la singularité physique du vivant. Paris : Hermann.
- Beatty, John (1995). « The evolutionary contingency thesis ». In : Concepts, theories, and rationality in the biological sciences, p. 45-81.
- Bernard, Claude (1865). Introduction à l’étude de la médecine expérimentale. Paris : Baillière.
- Bich, Leonardo, Matteo Mossio et Ana M. Soto (2020). « Glycemia Regulation : From Feedback Loops to Organizational Closure ». In : Frontiers in Physiology11, p. 69. issn : 1664-042X. doi : 10.3389/fphys.2020.00069 .
- Byers, N. (1999). « E. Noether’s discovery of the deep connection between symmetries and conservation laws ». In : The heritage of Emmy Noether in algebra, geometry, and physics. T. 12. Israel mathematical conference. Tel Aviv, p. 67-81.
- Canguilhem, G. (1972). Le normal et le pathologique. Paris : Presses Universitaires de France.
- Darwin, Charles (1859). On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life. London : John Murray.
- Douady, S. et Y. Couder (1996). « Phyllotaxis as a Dynamical Self Organizing Process Part I : The Spiral Modes Resulting from Time-Periodic Iterations ». In : Journal of Theoretical Biology 178.3, p. 255-273. issn : 0022-5193. doi : 10.1006/jtbi.1996.0024 .
- Gayon, Jean (1992). Darwin et l’après Darwin. Paris : Editions Kimé.
- Godfrey-Smith, Peter (1994). « A modern history theory of functions ». In : Noûs28.3, p. 344-362. doi : 10.2307/2216063 .
- Gould, S.J. (2002). The structure of evolutionary theory. Harvard University Press.
- Heisenberg, Werner (2010). La partie et le tout. Le monde de la physique atomique.Paris : Flammarion.
- Houle, David et al. (2011). « Measurement and meaning in biology ». In : The Quarterly Review of Biology 86.1, p. 3-34. doi : 10.1086/658408 .
- Kauffman, Stuart A (2019). A World Beyond Physics : The Emergence and Evolution of Life. New York : Oxford University Press.
- — (1993). The origins of order : Self organization and selection in evolution. New York : Oxford University Press.
- L’Héritier, Philippe (1949). Les méthodes statistiques dans l’expérimentation biologique. Paris : Centre National de la Recherche Scientifique.
- Lecointre, G. (2017). « Les contenants et les contenus : Que faire des invariants en biologie ? » In : Sciences de la vie, sciences de l’information. Sous la dir. de T. Gaudin et al. Paris : ISTE-Editions., p. 129-143. 2017.
- Letelier, J. C., G. Marin et J. Mpodozis (2003). « Autopoietic and (M,R) systems ». In : Journal of Theoretical Biology222.2, p. 261-272. issn : 0022-5193. doi : 10.1016/S0022-5193(03)00034-1 .
- Letelier, Juan-Carlos, María Luz Cárdenas et Athel Cornish-Bowden (2011). « From L’Homme Machine to metabolic closure : Steps towards understanding life ». In : Journal of Theoretical Biology 286.0, p. 100-113. issn : 0022-5193. doi : 10.1016/j.jtbi.2011.06.033 .
- Longo, G. (sept. 2018). « How Future Depends on Past and Rare Events in Systems of Life ». In : Foundations of Science23.3, p. 443-474. issn : 1572-8471. doi : 10.1007/s10699-017-9535-x .
- Longo, G. et Maël Montévil (2014). Perspectives on Organisms : Biological time, symmetries and singularities. Lecture Notes in Morphogenesis. Heidelberg : Springer. isbn : 978-3-642-35937-8. doi : 10.1007/978-3-642-35938-5 .
- Longo, G., Maël Montévil et S. Kauffman (juill. 2012). « No entailing laws, but enablement in the evolution of the biosphere ». In : Genetic and Evolutionary Computation Conference. GECCO’12. Philadelphia (PA, USA) : ACM. doi : 10.1145/2330784.2330946 .
- Miquel, Paul-Antoine et Su-Young Hwang (2016). « From physical to biological individuation ». In : Progress in Biophysics and Molecular Biology122.1, p. 51-57. issn : 0079-6107. doi : 10.1016/j.pbiomolbio.2016.07.002 .
- Montévil, Maël (2018). « A Primer on Mathematical Modeling in the Study of Organisms and Their Parts ». In : Systems Biology. Sous la dir. de Mariano Bizzarri. Methods in Molecular Biology. New York, NY : Springer New York, p. 41-55. isbn : 978-1-4939-7456-6. doi : 10.1007/978-1-4939-7456-6_4 .
- — (avr. 2019a). « Measurement in biology is methodized by theory ». In : Biology & Philosophy34.3, p. 35. issn : 1572-8404. doi : 10.1007/s10539-019-9687-x .
- — (nov. 2019b). « Possibility spaces and the notion of novelty : from music to biology ». In : Synthese196.11, p. 4555-4581. issn : 1573-0964. doi : 10.1007/s11229-017-1668-5 .
- Montévil, Maël et Matteo Mossio (2015). « Biological organisation as closure of constraints ». In : Journal of Theoretical Biology372, p. 179-191. issn : 0022-5193. doi : 10.1016/j.jtbi.2015.02.029 .
- Montévil, Maël, Matteo Mossio et al. (2016). « Theoretical principles for biology : Variation ». In : Progress in Biophysics and Molecular Biology122.1, p. 36-50. issn : 0079-6107. doi : 10.1016/j.pbiomolbio.2016.08.005 .
- Montévil, Maël, L. Speroni et al. (2016). « Modeling mammary organogenesis from biological first principles : Cells and their physical constraints ». In : Progress in Biophysics and Molecular Biology 122.1, p. 58-69. issn : 0079-6107. doi : 10.1016/j.pbiomolbio.2016.08.004 .
- Mossio, Matteo, C. Saborido et A. Moreno (2009). « An organizational account of biological functions ». In : The British Journal for the Philosophy of Science60.4, p. 813-841. doi : 10.1093/bjps/axp036 .
- Papadopoulos, Dimitri et al. (1999). « Genomic evolution during a 10,000-generation experiment with bacteria ». In : Proceedings of the National Academy of Sciences96.7, p. 3807-3812. issn : 0027-8424. doi : 10.1073/pnas.96.7.3807 . eprint : https://www.pnas.org/content/96/7/3807.full.pdf .
- Rosen, R. (1991). Life itself : a comprehensive inquiry into the nature, origin, and fabrication of life. New York : Columbia University Press.
- Ruiz-Mirazo, K. et A. Moreno (juin 2004). « Basic Autonomy As a Fundamental Step in the Synthesis of Life ». In : Artif. Life10.3, p. 235-259. issn : 1064-5462. doi : 10.1162/1064546041255584 .
- Schrödinger, E. (1944). What Is Life?Londre : Cambridge University Press.
- Soto, Ana M. et al. (2016). « From the century of the genome to the century of the organism : New theoretical approaches ». In : Progress in Biophysics and Molecular Biology, Special issue, p. 1-82.
- Stiegler, Barbara (2015). « L’hommage de Stephen Jay Gould à l’évolutionnisme de Nietzsche ». In : Dialogue54.3, p. 409-453. doi : 10.1017/S0012217315000864 .
- Strocchi, F. (2005). Symmetry breaking. T. 732. Lecture Notes in Physics. Heidelberg : Springer Verlag. doi : 10.1007/b95211 .
- Thom, René (1974). Modèles mathématiques de la morphogenèse. Paris : Union Générale d’Éditions.
- Thompson, D’A. W (1942). On growth and form. Cambridge : Cambridge University Press.
- Turing, A. M. (1952). « The Chemical Basis of Morphogenesis ». In : Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 237.641, p. 37-72. doi : 10.1098/rstb.1952.0012 .
- Van Fraassen, B.C. (1989). Laws and symmetry. Oxford University Press, USA.
- Varela, F.J., H.R. Maturana et R. Uribe (1974). « Autopoiesis : The organization of living systems, its characterization and a model ». In : Biosystems5.4, p. 187-196. issn : 0303-2647. doi : 10.1016/0303-2647(74)90031-8 .