Modeling organogenesis from biological first principles
Organization in biology
Here we discuss the application and articulation of biological principles for mathematical modeling of morphogenesis in the case of mammary ductal morphogenesis, with an emphasis on the default state.
Abstract
Unlike inert objects, organisms and their cells have the ability to initiate activity by themselves, and thus change their properties or states even in the absence of an external cause. This crucial difference led us to search for principles suitable for the study organisms. We propose that cells follow the default state of proliferation with variation and motility, a principle of biological inertia. This means that in the presence of sufficient nutrients, cells will express their default state. We also propose a principle of variation that addresses two central features of organisms, variation and historicity. To address interdependence between parts, we use a third principle, the principle of organization: more specifically, the notion of the closure of constraints. Within this theoretical framework, constraints are specific theoretical entities defined by their relative stability with respect to the processes they constrain. Constraints are mutually dependent in an organized system and act on the default state.
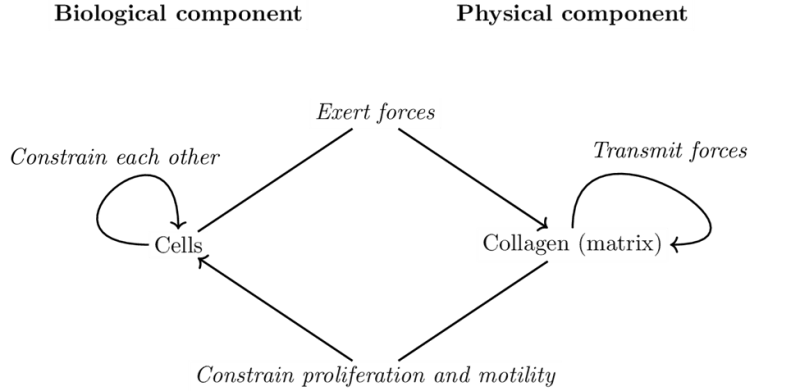
Here we discuss the application and articulation of these principles for mathematical modeling of morphogenesis in a specific case, that of mammary ductal morphogenesis, with an emphasis on the default state. Our model has both a biological component, the cells, and a physical component, the matrix that contains collagen fibers. Cells are agents that move and proliferate unless constrained; they exert mechanical forces that i) act on collagen fibers and ii) on other cells. As fibers are organized, they constrain the cells’ ability to move and to proliferate. This model exhibits a circularity that can be interpreted in terms of the closure of constraints. Implementing our mathematical model shows that constraints to the default state are sufficient to explain the formation of mammary epithelial structures. Finally, the success of this modeling effort suggests a step-wise approach whereby additional constraints imposed by the tissue and the organism can be examined in silico and rigorously tested by in vitro and in vivo experiments, in accordance with the organicist perspective we embrace.
Table of contents
Reading time: ~51 min
- 1. Introduction
- 2. Background concepts
- 3. From organicist ideas to principles for a theory of organisms
- 4. The mammary gland as an organ model for the study of morphogenesis
- 5. From the 3D culture model to a mathematical model
- 6. Mathematical Model
- 7. The in vitro system and the organism
- 8. Conclusions
- Acknowledgements
- Bibliography
Modeling organogenesis from biological first principles
1 Centre Cavaillès, République des Savoirs UAR3608, CNRS, Collège de France et École Normale Supérieure, Paris, France
2 Tufts University School of Medicine, Boston, United States of America
Abstract
Unlike inert objects, organisms and their cells have the ability to initiate activity by themselves, and thus change their properties or states even in the absence of an external cause. This crucial difference led us to search for principles suitable for the study organisms. We propose that cells follow the default state of proliferation with variation and motility, a principle of biological inertia. This means that in the presence of sufficient nutrients, cells will express their default state. We also propose a principle of variation that addresses two central features of organisms, variation and historicity. To address interdependence between parts, we use a third principle, the principle of organization: more specifically, the notion of the closure of constraints. Within this theoretical framework, constraints are specific theoretical entities defined by their relative stability with respect to the processes they constrain. Constraints are mutually dependent in an organized system and act on the default state.
Here we discuss the application and articulation of these principles for mathematical modeling of morphogenesis in a specific case, that of mammary ductal morphogenesis, with an emphasis on the default state. Our model has both a biological component, the cells, and a physical component, the matrix that contains collagen fibers. Cells are agents that move and proliferate unless constrained; they exert mechanical forces that i) act on collagen fibers and ii) on other cells. As fibers are organized, they constrain the cells' ability to move and to proliferate. This model exhibits a circularity that can be interpreted in terms of the closure of constraints. Implementing our mathematical model shows that constraints to the default state are sufficient to explain the formation of mammary epithelial structures. Finally, the success of this modeling effort suggests a step-wise approach whereby additional constraints imposed by the tissue and the organism can be examined in silico and rigorously tested by in vitro and in vivo experiments, in accordance with the organicist perspective we embrace.
1. Introduction
Throughout the 20th century biology underwent changes that little by little removed concepts which up until that time were considered to be the main characteristics of organisms, such as agency, normativity and goal-directedness. Later on, even the concept “organism” was deemed superfluous and almost disappeared from biological theory as the idea of a genetic program gained acceptance (Nicholson 2014). At the turn of the new millennium critical appraisals of the reductionist stance of the molecular biology revolution became more numerous, both regarding the espousing of 19th century physicalism, and the questionable adoption of mathematical theories of information and the notions of program and signal (Longo, Miquel et al. 2012). In addition to their critical analysis of the status quo, some biologists proposed alternative stances regarding organismal and evolutionary biology (Sonnenschein and Soto 1999; Oyama 2000; Kupiec and Sonigo 2003; Moss 2003; Jablonka and Lamb 2005; Noble 2006). It was clear to many that the promised reduction of biology to chemistry and physics was just a misplaced aspiration that did not translate into advances in experimental biology; various authors suggested alternatives. An alternative, both philosophical and theoretical, was to abandon reductionism by returning to organicism (Gilbert and Sarkar 2000; Greenspan 2001; Soto and Sonnenschein 2005). Theoretical biologists inspired by an organicist stance started to reintroduce the very notions into biology that distinguished living matter from the inert, namely, agency (Kauffman 2001). Another proposed alternative was technological, namely, the collection of data but at a larger scale (-omics). The idea was to transfer the task of making sense of phenomena to computers and data scientists by generating hypotheses from the data patterns revealed by such analysis (Bassett, Eisen et al. 1999; Brown and Botstein 1999). Another approach used the application of mathematical modeling, particularly various forms of “pragmatic systems biology” to search for molecular interactions (O'Malley and Dupre 2005). Neither one of these technological fixes produced the expected advances in experimental biology; the theoretical work of the organicists, instead, has started to impact experimental work via mathematical modeling based on biological principles (Montévil, Speroni et al. 2016) and conceptual analysis (Bich, Mossio et al. 2020).
In spite of these critical criticisms, the current practice of developmental biology is still guided by the metaphoric use of the mathematical concepts of information, program and signal, particularly the idea of a teleonomic genetic program, shaped by natural selection. Determination of the organism follows from this program and thus is extrinsic to the developing organism as such. The developmental program is supposed to drive the developing organism toward a final state, thus defining development as an apparently goal-oriented process. This genocentric view, which endows genes with a privileged causal role, suffers from many weaknesses (Longo, Miquel et al. 2012; Longo and Mossio 2020; Soto and Sonnenschein 2020). It falls short of providing an understanding of how a complex, fully organized biological entity will systematically be formed from this putative “program”, where such a program is located, and how it is executed. One main reason behind these shortcomings is that while there is a close relationship between a DNA sequence and the corresponding protein, there is no such correspondence between genes and phenotypes because the possible properties of phenotypes are not prestatable (Moss 2008). Consequently, the relationship between genes and forms is not straightforward (Soto and Sonnenschein 2005). Moreover, the genetic program fails to account for the variability observed throughout embryogenesis and morphogenesis, which contradicts the invariance expected from a “program”, as exemplified by developmental plasticity (West-Eberhard 2003). Additionally, because of this reliance on the genetic program, contemporary developmental biology tends to address causality in mechanistic terms, which conflicts with the interdependence between the whole, namely the developing organism, and its parts (Soto and Sonnenschein 2020). All these difficulties call for a reappraisal of the philosophical and theoretical frames that guide contemporary research in development in general and morphogenesis in particular. This essay will briefly discuss the concepts and theoretical frames that we use to construct a principle-based modeling of developmental and physiological processes. This will be illustrated by recent work on mathematical modeling of mammary gland morphogenesis.
2. Background concepts
While reductionism became the dominant philosophical stance in 20th century biology, a movement named “Organicism” developed during the period between the two world wars. Organicism is a philosophical stance committed to the following general ideas: 1) the centrality of the organism concept in biological explanation; 2) the importance of organization as a theoretical principle; and 3) the vindication of the autonomy of biology as a science (Nicholson and Gawne 2015).
Organicism is a materialistic philosophical stance whereby new properties that could not have been predicted from the analysis of the lower levels appear at each level of biological organization. Also, implicit in this view is the idea that organisms are not just “things” but objects under relentless change. While reductionist stances are usually derived from an ontology of unchanging substances, i.e., “being”, organicist stances are usually focused on an ontology of “becoming” (Dupré and Nicholson 2018).
In the 1970's while molecular biologists aspired to reduce biology to chemistry, advances in the understanding of dissipative non-equilibrium physical systems that self-organize influenced theoretical biologists interested in biological organization. Many of these thinkers, such as S. Kauffman, H. Maturana and F. Varela, went beyond the notion of far from equilibrium systems and were inspired by the Kantian concept of biological organization that stressed the interrelatedness of the organism and its parts and the circular causality implied by this relationship (an organism is the cause and effect of itself). Recognizing that Kantian organization does not correspond to the spontaneous self-organization of physical systems they worked out a new regime of circular causation. In this circular organization regime, the parts depend on the whole and vice versa; this regime not only produces and maintains the parts that contribute to the functioning of the whole integrated system, but the integrated system also interacts with its environment to promote the conditions of its own existence. This view of organization neatly leads to conceiving intrinsic teleology as a concept compatible with scientific causality (Mossio and Bich 2017). We can understand organisms as normative agents with the main aim of keeping themselves alive; their proper understanding requiring teleological principles of explanation. In the remainder of this section, we briefly delineate the main concepts in addition to organization and teleology that guide our efforts.
Historicity: While physical self-organizing systems like flames and micelles appear spontaneously, organisms are generated by the reproduction of a pre-existing organism. Historicity is fundamental to phylogenesis and ontogenesis. Historicity particularity establishes a difference from the theoretical frameworks of physics and creates methodological and theoretical challenges for mathematization in biology. Moreover, the historicity of organisms encompasses two-time scales, the long scale of phylogeny and the short of ontogeny. Consequently, historical analysis is central to the understanding of biological organization (Longo and Soto 2016; Montévil 2020).
Distinctive materiality: Organisms are made up of chemicals such as DNAs, RNAs, proteins and membranes. Unlike computer programs (software) that are independent of the materials of the “hardware”, the functions an organism accomplishes cannot be dissociated from the particular materials the organism is comprised of (Longo and Soto 2016). This view precludes the software-hardware dualism from biological entities. The materiality of biological objects also has an epistemological dimension. This is evidenced by comparing physical objects with biological ones. In physics, objects are primarily defined by abstract mathematical constructs, as illustrated by the definition of the speed of light in a vacuum being the speed of any light ray. In contrast, biological objects are defined by referencing a particular specimen of an organism, the type, to which the scientific name of a species is formally attached. This specific materiality trickles down to all biological practices, so that biological objects are always defined in reference to concrete objects rather than to theoretical abstractions (Montévil 2019).
Agency and normativity: Teleology is associated with the notions of autonomy and normative agency. The purposiveness of living entities is considered a consequence of the architecture of adaptive systems (Walsh 2015). Organisms are normative agents; namely, they have the capacity to generate actions and their own rules. Normative agency is a major characteristic that differentiates living from inert objects. Organisms undergo individuation which is manifested in their ability to change their own organization, that is, change their own rules. Another remarkable characteristic of organisms is their propensity to become sick and to overcome disease; pathology is an exclusively biological discipline (Canguilhem 1991).
Specificity. Physical theories describe generic objects fitting a mathematical construct; for example, as mentioned above, when one refers to the speed of light in a vacuum there is no need to refer to a specific ray of light, as all travel at the same speed – an invariant of Einstein's relativities. Of course, the methodological approach of physics can accommodate a variety of situations, like phase transition and crystallization however, always under the umbrella of a generic description that goes with mathematization. In contrast, biological objects are specific; for example, organisms are individuals in the process of undergoing further individuation. In other words, they are the result of history and continue to generate historical novelties. While variation in physical objects is merely a result of quantitative changes, in biology, in addition to the latter, variation is an intrinsic characteristic of organisms which plays a major role in evolutionary biology as the substrate of natural selection and in ontogenesis as the source of functional novelty (Longo and Montévil 2011; Longo and Soto 2016; Montévil, Mossio et al. 2016). Reductionist attribute a a form of specificity to molecules (which are assumed to be defined by their structure, thus, they are ultimately generic), consequently eluding the epistemological challenge of working with specific objects. In contrast, the organicist perspective locates specificity in biological objects endowed with autonomy, that is, organisms and their cells. Cellular specificity is the result of the particular trajectory of each cell during embryogenesis, namely, its interactions with other cells as it proliferates and migrates during histogenesis and organogenesis.
Constraints: Biological specificity does not negate the idea that aspects and parts of organisms are endowed with a kind of restricted genericity, namely, limited invariance. We call these elements constraints. An example of a constraint is the structure of articulations between bones which preclude certain movements and allow others. Typically, constraints may change over a longer time scale than the process they constrain. For example, the concentration of an enzyme does not change during the time it takes to catalyze the conversion of a substrate into products. Unlike physical invariants that are postulated and stem from fundamental principles, the existence of biological constraints requires explanations (by evolution and organization).
3. From organicist ideas to principles for a theory of organisms
Scientific theories provide organizing principles and construct objectivity by framing observations and experiments (Longo and Soto 2016). Theories construct the proper observables and provide the framework for studying them. The usefulness of theories is not determined by their being “right”. Even a “wrong” theory can be useful if, when proven incorrect it is modified or dismissed. The limiting factor for being useful is that a theory should not be vague, as vague theories cannot be proven to be incorrect (Feynman 2017).
A theoretical principle of biological “inertia”, the default state of cells. A method used to develop a theoretical framework consists of positing what takes place when nothing is done to a system, that is, when discussing default states. For example, the inertial state of classical mechanics corresponds to the trajectory of an isolated object. In biology, we posit that the default state of cells is proliferation with variation and motility. It is based on the cell theory and it relates to the specific materiality of the alive. The default state is a manifestation of the agency of living objects, and thus, a cause (Longo, Montévil et al. 2015). In contrast to physical objects, the presence of sufficient nutrients is required to maintain the metabolic needs, keeping the biological object alive. In these inertial conditions cells move and proliferate generating variation (Soto, Longo et al. 2016; Sonnenschein and Soto 2021). Moreover, in the same way that the departure of inertia enables physicists to define classical forces as cause, the departure from the default state defines what causes are. It follows that there are two causal levels in the default state: the level of proliferation and motility that comes from objects understood as specific objects (i.e. causality at the level of cells as such), and the level of constraints acting on the default state (i.e. constraints acting on cells).
The principle of organization by closure of constraints. In an organism, constraints depend collectively on each other thus generating a circle of dependencies called closure (Montévil and Mossio 2015; Mossio, Montévil et al. 2016). In turn, closure provides an understanding of the relative stability of constraints and more generally of biological organizations. Moreover, the principle of organization leads to the identification of specific constraints in an organism, and to assess whether a given constraint is functional, that is, it participates in closure.
The principle of variation. An implicit but overarching principle in physics is that we can understand the changes of an object by means of invariants and invariant preserving transformations (symmetries). For example, an inertial trajectory preserves momentum, energy, etc. This perspective is the basis for understanding physical objects as generic objects. By contrast, the principle of variation posits that biological objects are specific, and therefore relevant invariants and symmetries typically change over time. Modelers sometimes propose to accommodate biological objects with mathematical constructs that would change over time; these changes are somewhat similar to the phase transitions of physics. However, such a construct would again define a generic object, and assume that we can prestate the possible changes taking place. Instead, it is not possible to identify the objects of an experiment, let's say a group of mice, with a mathematical construct that would accommodate the way they are organized on theoretical grounds. In other words, alternatives are always possible. As a result, biology must reason with a different kind of object when compared to physics, namely, specific objects.
Variation relates to the historicity of biological objects and their contextuality. Historicity stems from the historical accumulation of variations that, by creating novelty, co-define present biological organization. Contextuality is related to historicity because understanding the historical changes that formed current organisms requires knowledge of the context that facilitated these changes. Contextuality is obviously also relevant at the time of observation because the definition of experimental objects depends on the context in which they are found. Different contexts may entail different organizations. For example, during embryogenesis the relationship of a cell with its environment, namely the surrounding extracellular matrix and the neighboring cells, is a major determinant of the morphology and function of this cell within the organ in which it resides. Indeed, understanding a biological organization requires taking into account its interaction with the surrounding environment, both at a given time-point and through the successive environments that the biological object traverses (Soto and Sonnenschein 2005; Miquel and Hwang 2016; Montévil, Mossio et al. 2016; Sonnenschein and Soto 2016; Montévil 2019).
Overall, these three principles provide a framework for understanding both general aspects of biology and particular biological situations. Building on the organicist and evolutionist traditions they represent the beginning of novel thinking about principles and their applications (Soto, Longo et al. 2016).
A recent addition to this theory-building process is a symbol, χ, to accommodate specific objects as such. The crucial point is that this symbol does not play the same role as the variable of mathematics, instead it refers to a material object and the objects that are related to it, in a manner that is compatible with the phylogenetic method of classifying living beings (Montévil and Mossio 2020). It follows that this symbol is also a way of writing about specific objects such as cells on which constraints may act. Additionally, χ is a point of entry for modifications of an organization. As such, it represents the entry of diachronicity into the synchronic closure of constraints.
4. The mammary gland as an organ model for the study of morphogenesis
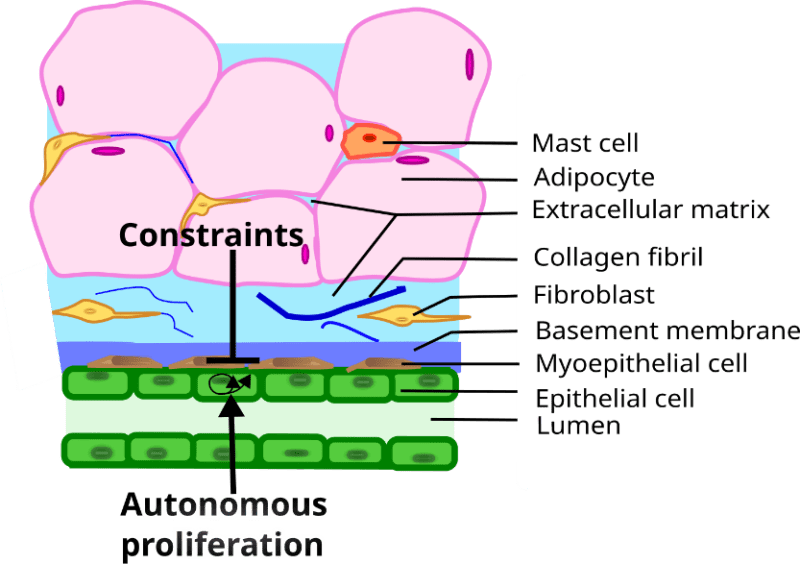
Let us now show how the theoretical framework summarized above can be applied to the study of morphogenesis in general, as well as that of different organs, for example, the mammary gland. Mammary glands are an evolutionary novelty of such importance that they define the class Mammalia. The gland is made up of two main components, namely, (1) the epithelial parenchyma, represented by the epithelial cells, whose function it is to produce and secrete milk to nourish the growing newborn, and (2) the stroma which surrounds the epithelium. The epithelium is composed of two layers of cells: a continuous luminal cuboidal cell layer and a basally located discontinuous myoepithelial cell layer. The stroma surrounding the epithelium is composed of various cell types (fibroblasts, adipocytes, and immune cells), blood vessels, nerves, lymph vessels, and an extracellular fibrous matrix of which the main component is collagen (Howard and Gusterson 2000; Masso-Welch, Darcy et al. 2000; Richert, Schwertfeger et al. 2000) (Figure 1). In the resting gland the epithelial compartment consists of a ductal system. During pregnancy alveoli grow from the ducts and these structures produce and secrete milk. Reciprocal interactions between the epithelium and the stroma mediate the development, function and remodeling of the mammary glands. The development of the organ can be divided into the following stages: fetal, pre-pubertal, pubertal, pregnancy, lactation and involution. Ovarian and pituitary hormones regulate the morphology and function of the gland during puberty and adult life, but the fetal and prepubertal isometric development is not hormone-dependent (Soto, Brisken et al. 2013). Disruption of epithelial-stromal interactions results in various pathologies including neoplasms (Soto and Sonnenschein 2011; Sonnenschein and Soto 2020).
4.1 A 3D culture model for the study of mammary gland morphogenesis
3D models aim to mimic in vivo conditions while reducing the number of organismal constraints to those which are hypothesized to be the most relevant ones for the purpose of the study. This approach allows the researcher to obtain results from which to estimate the contribution of these components to morphogenesis and/or physiology of the gland inside the organism. Simpler models may then be compared to more complex ones by adding other components. Ultimately, these models must be compared to the behavior of the gland in situ.
Let's now discuss how our theoretical frame guides our strategy. Our theoretical proposition profoundly modifies both modeling and experimental practices. A main objective of this section is to discuss the theoretical determination of the object of study. It requires locating the part (i.e., the mammary gland) into a model of the whole (i.e., the organism). Prior to working on the isolated part ('ecti-1000), choices must be made regarding what to extract from the whole (Bich, Mossio et al. 2020). Then, we identify the process that we aim to elucidate; in this case, ductal morphogenesis, where given classes of constraints emerge, such as epithelial structures similar to ducts (which have a geometric feature, undergo cell polarization while developing a lumen). We next hypothesize that some elements are critical, and to an extent, sufficient for this process: some constraints, such as collagen type-I fibers, and some specific objects, here epithelial cells from suitable cell lines. This simplification is only possible in a given context that roughly mimics the outcome of critical physiological processes: an incubator for temperature, CO2, sterility, and humidity, media for the chemical milieu, including nutrients, and an extracellular matrix that allows the growth in 3D of the cells into structures. Now, even if such conditions are sufficient for the intended constraints to emerge in vitro, it does not follow that these elements provide a full understanding of the actual phenomenon, and the integration in the organism (with more complex in vitro experiments) is critical to genuinely understand it.
Herein we use a human breast epithelial cell line, MCF10 cells embedded in 3D matrices containing only collagen-I or constant concentrations of collagen-I and variable concentrations of a mixture of basement membrane proteins (Matrigel); these components of the mammary stroma allow for breast epithelial cells to organize into structures that closely resemble those observed in vivo (Figure 2) (Krause, Maffini et al. 2008; Dhimolea, Maffini et al. 2010; Krause, Jondeau-Cabaton et al. 2012; Barnes, Speroni et al. 2014; Speroni, Whitt et al. 2014).

5. From the 3D culture model to a mathematical model
To understand the morphogenesis taking place in 3D culture, we methodically used the principle of the default state to build a first mathematical model and then a computational one (Montévil, Speroni et al. 2016).
5.1 Proliferation
Breast estrogen-target epithelial cells express their default state proliferating maximally in serumless medium. Addition of hormone-free serum (or serum albumin, the inhibitor of cell proliferation present in serum) to the culture medium results in a dose-dependent inhibition of cell proliferation. This inhibitory constraint could be removed by lowering the albumin concentration or by adding estrogens (Sonnenschein, Soto et al. 1996). Additional constraints are those imposed by cell-cell contact and more generally the mechanical properties of the cells and the matrix in which they are embedded (Barnes, Speroni et al. 2014).
5.2 Motility and constraints to motility
In biology, cells are agents, they generate forces and initiate motion. They proliferate and move unless there are constraints which prevent them from doing so. In general, classical mechanics imposes that cells exert forces on something to move, and the way they can exert forces depends on their history, both history at the evolutionary level and the history of their lineage inside the organism (and in laboratories in the case of established cell lines). Specifically, breast epithelial cells need a support to crawl on since they do not have a flagellum or a functionally analogous set of constraints. Notably, they use fibers to which they can attach and that they can pull in order to move. Moreover, cells are not simple mechanical structures that remain invariant over time, they react in a diverse manner to a mechanical force, depending on their history and normativity. For example, mechanical compression induces the expression of a set of genes (Soto, Sonnenschein et al. 2008; Longo and Montévil 2014).
The constraints to motility that cells experience in situ can be modeled in a 3D culture system. The matrix in which the cells are seeded mimics the tissue environment. Once embedded in a matrix, breast epithelial cells emit projections, like filopodia and pseudopodia, which are used for motility; matrix composition may facilitate or hinder the ability of these projections to generate locomotion (Figure 3).
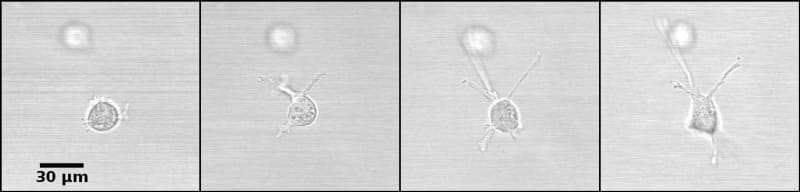
In a fibrillar matrix, these projections can attach to fibers and exert forces on them. This activity leads to cell elongation and later to the appearance of structures geometrically akin to ducts (Barnes, Speroni et al. 2014). Similarly, cells use these projections for locomotion. The latter is constrained notably by adhesion to other cells, but also by the space occupied by the matrix. Specifically, pore size and matrix rigidity are constraints on cell migration. Pores are larger in the fibrillar matrix than in the globular matrix, while the latter is stiffer than the fibrillar matrix (Barnes, Speroni et al. 2014). It follows that these properties contribute to morphological differences among epithelial structures.
Breast epithelial cells growing in a globular matrix emit short projections into the matrix that retract soon afterwards and display limited motility (Montévil, Speroni et al. 2016). Cells rotate and divide resulting in the formation of an acinus, a sphere with a central lumen (Tanner, Mori et al. 2012).
Cells that touch each other, whether as a result of migration or after cell division, can attach to each other. Adhesion, and more specifically the physico-chemical structures involved, constrain cell movements. Moreover, during morphogenesis, cells may detach from a structure and later reintegrate with it (Barnes, Speroni et al. 2014).
5.3 Determination of the system
Cells are specific objects and should therefore be modeled by including the χ symbol (Montévil and Mossio 2020). Unlike properties in physics, which are described by their causal relations and their underlying invariants, χ is defined by its past, including past contexts, for example the common ancestor of a population of laboratory animals. This symbol enables us to transcribe with theoretical accuracy what we know about the objects involved, for instance the cells are from a given cell line that may be found at a specific place and that have been grown in a given context for several generations. At the time of the publication of our first model, these methodological problems were raised by the principle of variation; we are now ready to use the χ symbol to address this problem in theoretical writing; our model is undergoing a formal rework.
In the biological model, causality takes place in different ways. The default state of cells frames how objects designated by χ proliferate. The departure from the default state describes how constraints act on cells, that is, objects designated by χ. Finally, constraints acting together, here mainly in the matrix, are analyzed in a more standard biophysical manner – except that they are in relation to cells. An example of such a constraint is collagen orientation with respect to force transmission.
Specifically, following the default state, cells proliferate, leading to an increase in cell number. Cell accumulation has several consequences: the redistribution of fluids, compression of matrix and/or matrix degradation. Cells exert the other component of the default state, motility, by exerting forces on the matrix if they can do so. In Matrigel rich matrices, cells cannot attach to the matrix and this component of the default state is constrained. That is, cells emit filopodia and exert their motility but cannot migrate. By contrast, in collagen matrices, cells grab fibers and exert forces on them, leading to changes in fiber organization (Dhimolea, Maffini et al. 2010)). The forces propagate in the matrix depending on its specific state (i.e. fiber orientations), and can reach over long ranges (Guo, Ouyang et al. 2012). As fiber organizations change, so do the constraints that they exert on cells. At the beginning of the formation of a structure, there is a symmetry breaking that leads to the emergence of a main direction in which forces are exerted (the direction of the elongated structure). In particular, forces exerted by cells on each other and on the structure's tips also constrain the default state due to the strain that follows from this force (Figure 4). Collagen bundles facilitate the merging of epithelial structures initially positioned at a long distance range (Guo, Ouyang et al. 2012).
6. Mathematical Model
Mathematical modeling of biological phenomena is usually practiced using principles from one discipline (i.e., physics) and applying them to biology without evaluating the theoretical meaning these principles have when transported into the theoretical context of biology. It follows that, when models include cells as elementary components, the latter are described by ad hoc hypotheses that we reviewed elsewhere (Montévil, Speroni et al. 2016). This modus operandi is properly interpreted as imitation (Turing 1950); stricto sensu mathematical modeling must be based on the theoretical principles of the discipline being studied. Below we describe the mathematical model both from the theoretical framework provided by the principles and the analysis briefly described above.
The theoretical framework restricts what is acceptable in order to model cellular behaviors. For example, the absence of proliferation requires constraints and quiescence cannot follow from ad hoc rules describing cells in agent-based modeling. More generally, it means that mathematical modeling, in this iteration, is about the interplay between the default state and the constraints acting on it (principle of organization); thus, it is not admissible for models of cells to follow arbitrary computational rules.
6.1 Description of the model
In this initial model, we opted for a macroscopic and mesoscopic description of the 3D cultures, meaning that we described cells as elementary units and the fibers by their local orientation in a small spatial volume. We used agent-based modeling for cells and lattice modeling for fibers (limited to fiber orientation), mechanical forces, and a hypothetical chemical inhibitor of cell proliferation. The later seemed to be required to understand some aspect of the biological model, and this fact is also an illustration that theoretical principles constrain mathematical modeling and lead to the formulation of hypotheses.
The core and the originality of the model resides in our the method of understanding cell behavior. First comes the modeling of the default state, a modeling that evolves and expands in future works with the introduction of χ. Cells proliferate after a fixed time, unless constrained. One of the two cells produced by cell division occupies a random adjacent position to the mother cell while the other occupies the position of the mother cell. Motility, instead, is more complex to model. Cells move unless constrained, according to the default state. When the cell environment is symmetric, this motion is random. Moreover, motility also encompasses the forces exerted on adjacent cells and extracellular matrix. The latter depends on the force exerted by cells, the orientation of the cytoskeleton, and that of the neighboring fibers.
Second comes the modeling of the constraints on cell proliferation and motility. As mentioned, proliferation requires that space is available for the new cell. Proliferation tends to occur along the direction of forces, so that a cell under a significant mechanical strain may not be able to proliferate even when an adjacent free position exists. Third comes the modeling of the hypothetical chemical inhibitor which slows down proliferation and lessens movements.
Overall, even in this simple iteration, the default state leads to a practice of modeling where spontaneous cellular activity, endowed with randomness, is central. Constraints limit this randomness and orient cellular behavior towards structures that are functional in the organism's life cycle. Moreover, the relationship between the default state and constraints is not just a molding of cell behavior by constraints because the constraints are transformed by cells exerting their default state in a manner that depends on their historical path (both evolutionarily and inside the organism) – the outcome of this historical path is made explicit to an extent by intracellular constraints such as the cytoskeleton.
6.2 Outcomes of the mathematical model
Here, we are discussing the outcome of the initial model as described in Montévil et al. where the details of the model and the analysis can be found (Montévil, Speroni et al. 2016).
6.2.1: In a globular matrix
In globular matrix, cells cannot attach to the matrix, and therefore, cannot use it to move nor rearrange it. It follows that cells only exert forces on each other, and crawl on each other when not attached. As a result, cells proliferate and remain tightly together, leading to a spherical structure (Figure 5). Proliferation takes place at the periphery of the structure because cells inside stop proliferating due to the lack of available space. The structure stops growing after some time (due to the chemical inhibitor).
6.2.2 In a fibrillar matrix
In fibrillar matrices, things are a bit more complex because cells interact actively with the matrix and the latter constrains them. In the beginning, a single cell is surrounded by collagen, and it starts to pull on fibers, possibly moving, and the collagen tends to align with the direction of the force exerted. The structure gains additional cells by cell proliferation, and the new cells tend to remain together by cell adhesion (though some may escape the structure). By pulling on each other and on fibers, a dominant direction emerges. This direction is both influenced by the direction in which the first cells pull, but also by the random initial orientation of every part of the collagen. Mathematically, it comes from an instability leading to a symmetry breaking, so that any small asymmetry in the initial condition is amplified leading to a large system-wide dominant direction (Longo and Montévil 2018). Motility and proliferation are mostly constrained in this direction (due to the mechanical constraint imposed by this force). It follows that the structure becomes elongated. The chemical inhibitor, in combination with the mechanical forces, leads to a stop of the proliferation in the middle of the structure while the tips can continue to expand (Figure 5).

Due to the randomness used to model cellular behavior under constraints and the initial matrix, the elongated structure is not perfectly straight, but can form a curve-shaped structure. Moreover, the instability at the tip also sometimes allows the structure to branch (Figure 6). This outcome was not expected when establishing the model, and is a very interesting result of the method, as in the in vivo condition, the mammary gland ductal tree exhibits branching.

7. The in vitro system and the organism
By accepting the reciprocal relationship between the whole (organism) and its parts our theoretical proposition profoundly modifies both modeling and experimental practices. A main objective of our work is the theoretical determination of the object of study. This requires locating the part (i.e., the mammary gland) into a model of the whole (i.e., the organism), an operation that requires further modeling work. Prior to working on the isolated part ('ecti-1000), choices are made regarding what to extract from the whole. In this case, our model only dealt with epithelial cells and extracellular matrix. Next, results are compared with information gathered from observing the part within the organism. To bridge the gap between what is observed in the whole organism and in the in vitro model, we add other components of the mammary gland stepwise such as relevant cell types (i.e., mammary gland stromal fibroblasts). To grasp the organismal constraints that affect mammary gland development and function we add hormones to the model consisting of epithelial cells, fibroblasts and different matrices. We aim to identify primary constraints (Bich, Mossio et al. 2016) which in our model are the matrix with or without stromal fibroblasts, and regulatory constraints, which in our model are the mammotropic hormones (estradiol, progesterone, prolactin) (Bich, Mossio et al. 2020).
Regarding the role of mammotropic hormones, at the onset of puberty estrogen influences the formation of terminal end buds, the structure at the end of the ducts that invade the stroma and guide ductal growth. Progesterone promotes side-branching and prolactin facilitates alveolar development in preparation for lactation. The dominant reductionist approach focuses on the hormone-receptor interactions and consequent induction of gene expression inside the cell rather than searching to explain the shape changes of the epithelial structures resulting from these hormonal influences in the epithelial cells. Instead, by applying an organicist perspective using a hormone responsive cell line we found that exposure to hormones leads cells to modify the collagen fiber organization of the matrix in which they are embedded. This, in turn enables the cells to generate the distinct epithelial organization patterns observed in situ, namely estrogen-mediated ductal elongation, progesterone-mediated lateral branching and prolactin-mediated budding (Speroni, Whitt et al. 2014). In vitro 3D models can also be used to manipulate constraints beyond the range operating in vivo. For example, to learn how rigidity affects shape beyond the limits imposed by the organism Paszek et al. showed that by increasing the rigidity of the mammary gland model to mimic that of bone, lumen formation was inhibited and epithelial structures disorganized in a way reminiscent of neoplasms (Paszek, Zahir et al. 2005).
8. Conclusions
Experimental research guided by our global theoretical approach addresses different questions from those guided by the metaphors of information, signal and program borrowed from mathematical information theories (Longo and Montévil 2011). The use of information metaphors drives experimenters to search for causality in discrete structures such as molecules. Additionally, ignoring the circular interdependency of the organism and its parts while embracing the idea that explanations need to uncover “molecular” mechanisms precludes the identification of physical “constraints” which causally contribute to the generation and maintenance of the organism.
Some of these shortcomings have been addressed by a view that, to account for the acquisition of form, combines the genetic program with physical determinants. This view facilitates the introduction of mathematical modeling of morphogenesis whereby matter plays an active role in the stability of local processes and the appearance of shapes. Nevertheless, it has shortcomings: i) it addresses development, a phenomenon that results from a historical process, evolution, with tools designed to study spontaneous phenomena resulting from ahistorical laws, ii) it conflates theories of physics with existing models in physics and with the method of modeling of physics (Arias Del Angel, Nanjundiah et al. 2020), and finally, iii) purposiveness is still understood as genetic teleonomy (Montévil 2020).
Rather than applying the usual procedure of transferring mathematical structures developed for the understanding of physical phenomena into biological ones, we model biological processes from a biological theoretical framework. Here we base our approach on two principles (default state and principle of organization) of the three principles proposed as foundations for a theory of organisms. We have thus provided the proof of principle that mathematical modeling based on the theoretical framework of the discipline to which the modeled phenomenon pertains, namely biology, is feasible and provides biological insight.
In fact, the two principles (default state and constraints leading to closure) were sufficient to show the formation of ducts and acini. Cells generated forces that were transmitted to neighboring cells and collagen fibers, which in turn created constraints to movement and proliferation. Additionally, the model pointed to a target of future research, namely, the inhibitors of cell proliferation and motility which in this mathematical model are generated by the epithelial cells. For a better integration with the principle of variation and the historicity of cells, we are introducing the use of the new symbol χ. Finally, the success of this modeling effort performed as a “proof of principle” opens the possibility for a step-wise approach whereby additional constraints imposed by the tissue (additional cell types) and the organism (hormones) could be assessed in silico and rigorously tested by in vitro and in vivo experiments.
Acknowledgements
This work was conducted as part of the research project entitled, “Toward a science of intrinsic purposiveness: shaping development", supported by the Templeton Foundation (PI, AMS), and “Building bridges between natural and social sciences through the prism of a theory of organisms” during AMS tenure as a Fellow of the Institute for Advanced Studies of Nantes, France. Additional support to AMS was provided by Grant ES030045 from the U.S. National Institute of Environmental Health Sciences. The funders had no role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript. The authors are grateful to Cheryl Schaeberle and Victoria Bouffard for their critical input, and to the reviewers for their helpful suggestions. The authors have no competing financial interests to declare.
Bibliography
- Arias Del Angel, J. A., V. Nanjundiah, M. Benítez and S. A. Newman (2020). "Interplay of mesoscale physics and agent-like behaviors in the parallel evolution of aggregative multicellularity." Evodevo 11: 21.
- Barnes, C., L. Speroni, K. Quinn, M. Montévil, K. Saetzler, G. Bode-Animashaun, G. McKerr, I. Georgakoudi, S. Downes, C. Sonnenschein, C. V. Howard and A. M. Soto (2014). "From single cells to tissues: interactions between the matrix and human breast cells in real time." PLoS ONE 9: e93325.
- Bassett, D. E., Jr., M. B. Eisen and M. S. Boguski (1999). "Gene expression informatics - It's all in your mine." Nature Genetics 21: 51-55.
- Bich, L., M. Mossio, K. Ruiz-Mirazo and A. Moreno (2016). "Biological regulation: controlling the system from within." Biology & Philosophy 31: 237-265.
- Bich, L., M. Mossio and A. M. Soto (2020). "Glycemia Regulation: From Feedback Loops to Organizational Closure." Front Physiol 11: 69.
- Brown, P. O. and D. Botstein (1999). "Exploring the new world of the genome with DNA microarrays." Nature Genetics 21: 33-37.
- Canguilhem, G. (1991). The Normal and the Pathological. New York, Zone Books.
- Dhimolea, E., M. V. Maffini, A. M. Soto and C. Sonnenschein (2010). "The role of collagen reorganization on mammary epithelial morphogenesis in a 3D culture model." Biomaterials 31: 3622-3630.
- Dupré, J. and D. J. Nicholson (2018). A manifesto for a processual philosophy of biology. Everything Flows: Towards a Processual Philosophy of Biology. D. J. Nicholson and J. Dupre. Oxford, Oxford University Press.
- Feynman, R. (2017). The Character of Physical Law. Cambridge MA, MIT Press.
- Gilbert, S. F. and S. Sarkar (2000). "Embracing complexity: Organicism for the 21st century." Developmental Dynamics 219: 1-9.
- Greenspan, R. J. (2001). "The flexible genome." Nature Reviews: Genetics 2: 383-387.
- Guo, C. L., M. Ouyang, J. Y. Yu, J. Maslov, A. Price and C. Y. Shen (2012). "Long-range mechanical force enables self-assembly of epithelial tubular patterns." Proceedings of the National Academy of Science of the United States of America 109: 5576-5582.
- Howard, B. A. and B. A. Gusterson (2000). "Human breast development." Journal of Mammary Gland Biology and Neoplasia 5: 119-137.
- Jablonka, E. and M. J. Lamb (2005). Evolution in Four Dimensions. Cambridge, MIT Press.
- Kauffman, S. (2001). "Molecular autonomous agents." Philos Trans A Math Phys Eng Sci 361(1807): 1089-1099.
- Krause, S., A. Jondeau-Cabaton, E. Dhimolea, A. M. Soto, C. Sonnenschein and M. V. Maffini (2012). "Dual regulation of breast tubulogenesis using extracellular matrix composition and stromal cells." Tissue Eng Part A. 18: 520-532.
- Krause, S., M. V. Maffini, A. M. Soto and C. Sonnenschein (2008). "A novel 3D in vitro culture model to study stromal-epithelial interactions in the mammary gland." Tissue Engineering 14: 261-271.
- Kupiec, J. J. and P. Sonigo (2003). Ni Dieu ni gène. Pour une autre théorie de l'hérédité. Paris, Seuil.
- Longo, G., P. A. Miquel, C. Sonnenschein and A. M. Soto (2012). "Is information a proper observable for biological organization?" Prog.Biophys.Mol.Biol. 109: 108-114.
- Longo, G. and M. Montévil (2011). "From physics to biology by extending criticality and symmetry breakings." Prog.Biophys.Mol.Biol. 106: 340-347.
- Longo, G. and M. Montévil (2014). Perspectives on Organisms: Biological Time, Symmetries and Singularities. Berlin, Springer.
- Longo, G. and M. Montévil (2018). Comparing symmetries in models and simulations. Handbook of Model-Based Science. M. Dorato, L. Magnani and T. Bertolotti: 843-856.
- Longo, G., M. Montévil, C. Sonnenschein and A. M. Soto (2015). "In search of principles for a Theory of Organisms." J Biosci 40(5): 955-968.
- Longo, G. and M. Mossio (2020). "Geocentrism vs genocentrism: theories without metaphors, metaphors without theories." Interdisciplinary Science Reviews 45(3): 380-405.
- Longo, G. and A. M. Soto (2016). "Why do we need theories?" Prog Biophys Mol Biol 122(1): 4-10.
- Masso-Welch, P. A., K. M. Darcy, N. C. Stangle-Castor and M. M. Ip (2000). "A developmental atlas of rat mammary gland histology." Journal of Mammary Gland Biology and Neoplasia 5: 165-185.
- Miquel, P. A. and S. Y. Hwang (2016). "From physical to biological individuation." Prog Biophys Mol Biol 122(1): 51-57.
- Montévil, M. (2019). "Measurement in biology Is methodized by theory." Biology & Philosophy 34(3): 35.
- Montévil, M. (2020). "Historicity at the heart of biology." Theory Biosci.
- Montévil, M. and M. Mossio (2015). "Biological organisation as closure of constraints." J Theor Biol 372: 179-191.
- Montévil, M. and M. Mossio (2020). "The Identity of Organisms in Scientific Practice: Integrating Historical and Relational Conceptions." Front Physiol 11: 611.
- Montévil, M., M. Mossio, A. Pocheville and G. Longo (2016). "Theoretical principles for biology: Variation." Prog Biophys Mol Biol 122(1): 36-50.
- Montévil, M., L. Speroni, C. Sonnenschein and A. M. Soto (2016). "Modeling mammary organogenesis from biological first principles: Cells and their physical constraints." Prog Biophys Mol Biol 122(1): 58-69.
- Moss, L. (2003). What Genes Can't Do. Cambridge, MA, MIT Press.
- Moss, L. (2008). "The meanings of the gene and the future of the phenotype." Life Sci Soc Policy 4: 38.
- Mossio, M. and L. Bich (2017). "What makes biological organisation teleological?" Synthese 194: 1089-1114.
- Mossio, M., M. Montévil and G. Longo (2016). "Theoretical principles for biology: Organization." Prog Biophys Mol Biol 122(1): 24-35.
- Nicholson, D. J. (2014). "The return of the organism as a fundamental explanatory concept in biology." Philosophy Compass 9/5: 347-359.
- Nicholson, D. J. and R. Gawne (2015). "Neither logical empiricism nor vitalism, but organicism: what the philosophy of biology was." Hist Philos Life Sci 37(4): 345-381.
- Noble, D. (2006). The Music of Life: Biology beyond the Genome. Oxford, Oxford University Press.
- O'Malley, M. A. and J. Dupre (2005). "Fundamental issues in systems biology." BioEssays 27: 1270-1276.
- Oyama, S. (2000). The Ontogeny of Information: Developmental Systems and Evolution. Durham, Duke University Press.
- Paszek, M. J., N. Zahir, K. R. Johnson, J. N. Lakins, G. I. Rozenberg, A. Gefen, C. A. Reinhart-King, S. S. Margulies, M. Dembo, D. Boettiger, D. A. Hammer and V. M. Weaver (2005). "Tensional homeostasis and the malignant phenotype." Cancer Cell 8: 241-254.
- Richert, M. M., K. L. Schwertfeger, J. W. Ryder and S. M. Anderson (2000). "An atlas of mouse mammary gland development." Journal of Mammary Gland Biology and Neoplasia 5: 227-241.
- Sonnenschein, C. and A. M. Soto (1999). The Society of Cells: Cancer and Control of Cell Proliferation. New York, Springer Verlag.
- Sonnenschein, C. and A. M. Soto (2016). "Carcinogenesis explained within the context of a theory of organisms." Prog Biophys Mol Biol 122(1): 70-76.
- Sonnenschein, C. and A. M. Soto (2020). "Over a century of cancer research: Inconvenient truths and promising leads." PLoS Biol. 18(4): e3000670.
- Sonnenschein, C. and A. M. Soto (2021). "Control of cell proliferation: is the default state of cells quiescence or proliferation." Organisms 5(1): 33-42.
- Sonnenschein, C., A. M. Soto and C. L. Michaelson (1996). "Human serum albumin shares the properties of estrocolyone-I, the inhibitor of the proliferation of estrogen-target cells." Journal of Steroid Biochemistry and Molecular Biology 59: 147-154.
- Soto, A. M., C. Brisken, C. M. Schaeberle and C. Sonnenschein (2013). "Does cancer start in the womb? Altered mammary gland development and predisposition to breast cancer due to in utero exposure to endocrine disruptors." Journal of Mammary Gland Biology and Neoplasia 18: 199-208.
- Soto, A. M., G. Longo, P. A. Miquel, M. Montévil, M. Mossio, N. Perret, A. Pocheville and C. Sonnenschein (2016). "Toward a theory of organisms: Three founding principles in search of a useful integration." Prog Biophys Mol Biol 122(1): 77-82.
- Soto, A. M., G. Longo, M. Montévil and C. Sonnenschein (2016). "The biological default state of cell proliferation with variation and motility, a fundamental principle for a theory of organisms." Prog Biophys Mol Biol 122(1): 16-23.
- Soto, A. M. and C. Sonnenschein (2005). "Emergentism as a default: cancer as a problem of tissue organization." Journal of Biosciences 30: 103-118.
- Soto, A. M. and C. Sonnenschein (2011). "The tissue organization field theory of cancer: A testable replacement for the somatic mutation theory." BioEssays 33: 332-340.
- Soto, A. M. and C. Sonnenschein (2020). "Information, programme, signal: dead metaphors that negate the agency of organisms." Interdisciplinary Science Reviews 45: 331-343.
- Soto, A. M., C. Sonnenschein and P. A. Miquel (2008). "On physicalism and Downward Causation in Developmental and Cancer Biology." Acta Biotheoretica 56: 257-274.
- Speroni, L., G. S. Whitt, J. Xylas, K. P. Quinn, A. Jondeau-Cabaton, I. Georgakoudi, C. Sonnenschein and A. M. Soto (2014). "Hormonal regulation of epithelial organization in a 3D breast tissue culture model." Tissue Engineering Part C Methods 20: 42-51.
- Tanner, K., H. Mori, R. Mroue, A. Bruni-Cardoso and M. J. Bissell (2012). "Coherent angular motion in the establishment of multicellular architecture of glandular tissues." Proceedings of the National Academy of Science of the United States of America 109: 1973-1978.
- Turing, A. M. (1950). "I. Computing machinery and intelligence." Mind LIX(236): 433-460.
- Walsh, D. (2015). Organisms, Agency, and Evolution. Cambridge Cambridge University Press.
- West-Eberhard, M. J. (2003). Developmental Plasticity and Evolution. Oxford, Oxford University Press.