Comment le hasard façonne le vivant ?
Le hasard. Littérature, arts, sciences, philosophie
En biologie, le hasard est une notion essentielle pour comprendre les variations ; cependant, cette notion n'est généralement pas conceptualisée avec précision. Nous apportons ici quelques éléments allant dans ce sens.
Abstract
La physique possède plusieurs concepts de hasard qui reposent néanmoins tous sur l’idée que les possibilités sont données d’avance. En revanche, un nombre croissant de biologistes théoriciens cherchent à introduire la notion de nouvelles possibilités, c’est-à-dire des modifications de l’espace des possibles - une idée déjà discutée par Bergson et qui n’a pas été véritablement poursuivie scientifiquement jusqu’à récemment (sauf, en un sens, dans la systématique, c’est-à-dire la méthode de classification des êtres vivants).
Alors, le hasard opère au niveau des possibilités elles-mêmes et est à la base de l’historicité des objets biologiques. Nous soulignons que ce concept de hasard n’est pas seulement pertinent lorsqu’on cherche à prédire l’avenir. Au contraire, il façonne les organisations biologiques et les écosystèmes. À titre d’illustration, nous soutenons qu’une question cruciale de l’Anthropocène est la disruption des organisations biologiques que l’histoire naturelle a structurées, conduisant à un effondrement des possibilités biologiques.
Table of contents
Reading time: ~48 min
- Abstract
- 1 Causality and randomness
- 2 Comment le hasard est devenu la source des êtres vivants actuels
- 3 Vers le hasard comme apparition de nouveaux possibles
- 4 Une nouvelle méthode s’appuyant sur la variation biologique
- 5 Aspects généraux des nouveaux possibles en biologie
- 6 Comment le hasard fait s’effondrer la diversité biologique
- Remerciements
- Références
Comment le hasard façonne le vivant ?
Abstract
La physique possède plusieurs concepts de hasard qui reposent néanmoins tous sur l’idée que les possibilités sont données d’avance. En revanche, un nombre croissant de biologistes théoriciens cherchent à introduire la notion de nouvelles possibilités, c’est-à-dire des modifications de l’espace des possibles - une idée déjà discutée par Bergson et qui n’a pas été véritablement poursuivie scientifiquement jusqu’à récemment (sauf, en un sens, dans la systématique, c’est-à-dire la méthode de classification des êtres vivants).
Alors, le hasard opère au niveau des possibilités elles-mêmes et est à la base de l’historicité des objets biologiques. Nous soulignons que ce concept de hasard n’est pas seulement pertinent lorsqu’on cherche à prédire l’avenir. Au contraire, il façonne les organisations biologiques et les écosystèmes. À titre d’illustration, nous soutenons qu’une question cruciale de l’Anthropocène est la disruption des organisations biologiques que l’histoire naturelle a structurées, conduisant à un effondrement des possibilités biologiques.
1 Causality and randomness
Ce chapitre aborde comment le hasard est devenu un pilier de la biologie et en quoi sa conceptualisation précise reste un défi pour la biologie théorique actuelle, avec des applications aux enjeux de notre époque, communément appelée l’Anthropocène. Or le hasard est une notion complexe dans les sciences, et il est nécessaire pour notre propos de revenir brièvement sur son histoire en dehors de la biologie.
Le hasard est au carrefour de différentes questions. Tout d’abord, le hasard est lié à la causalité et, en un sens, un phénomène aléatoire n’est pas déductible à partir de causes. Vient ensuite les paris, avec les jeux d’argent et les assurances (historiquement, pour les bateaux de commerce pendant la colonisation) — et ici les calculs sont cruciaux. Les théories des probabilités ont été développées précisément pour fournir des mesures de l’aléatoire. Enfin vient la notion d’imprévisibilité, qui est la plus récente.
En sciences, ces différentes questions se combinent ... de presque toutes les manières possibles. Par exemple, les dynamiques dites chaotiques sont déterministes, donc dépourvues d’"aléa causal", mais imprévisibles. Pourquoi ? Ces situations singulières sont dues à deux raisons qui se combinent. Premièrement, la mesure en mécanique classique n’est jamais parfaite ; nous évaluons la position et la vitesse d’un objet que jusqu’à une certaine précision - c’est une question de principes, et non de technologie. Deuxièmement, aussi proches que soient deux conditions initiales, les trajectoires ultérieures vont diverger très rapidement (à une vitesse exponentielle). La combinaison de ces deux facteurs implique l’imprévisibilité ; de petites causes, même celles que nous ne pouvons pas mesurer, peuvent avoir des effets importants. C’est cette situation que l’on appelle communément l’effet papillon, l’idée qu’un papillon battant des ailes peut créer un ouragan ailleurs. C’est aussi pourquoi nous ne pouvons pas dire si le système solaire est stable ou si une planète en sera éjectée un jour.
Examinons un autre écart. En informatique, un ordinateur est déterministe et prévisible ; comme l’appelle Turing, c’est une machine à états discrets où l’accès à l’état peut être parfait. Cependant, l’aléatoire apparaît lorsque nous mettons ensemble différents ordinateurs théoriques (y compris les différents cœurs des processeurs actuels) car il n’y a aucune certitude sur le calcul qui sera le plus rapide. Cet aléa correspond bien à l’imprévisibilité, mais sa particularité est qu’il n’a pas de métrique (il n’y a pas de probabilités). Donnons-en un exemple pittoresque. Imaginez la simulation du vent qui agit sur le toit pour que les tuiles tombent. Imaginez également la simulation de la marche d’un piéton. Alors, si des cœurs différents effectuent ces deux simulations, la tuile du toit peut ou non tomber sur le piéton car la mise à jour des deux modèles n’est pas synchronisée (si elle est mal conçue). Alors, les informaticiens conçoivent généralement leur algorithme de manière à ce qu’il conduise aux résultats escomptés dans toutes les situations.
Néanmoins, en un sens, le hasard va toujours de pair avec l’imprévisibilité. Mais la relation entre ces deux notions différentes n’est pas tout à fait simple. Par exemple, le mouvement aléatoire des molécules conduit une délicieuse odeur à se propager dans une cuisine et au-delà. D’une manière générale, lorsque l’on étudie un gaz, comme le dit Boltzmann, le chaos moléculaire conduit le gaz à tendre vers la situation d’entropie maximale, qui est parfaitement prévisible. Dans le même ordre d’idées, le pur hasard probabiliste n’est pas la situation la plus imprévisible. Par exemple, les statistiques du jeu de pile ou face sont très bien connues, et nous pouvons faire des prédictions pour un grand nombre de lancers. Les probabilités se distinguent profondément de l’anomie, l’absence de normes ou de lois. Il en va de même dans le cas de la mécanique quantique, où les possibilités et les probabilités sont très bien définies. En revanche, la capacité des sondages dans une élection à prédire les résultats est au mieux limitée. L’une des raisons en est que les citoyens et les localités sont divers, et que la capacité des sondages à échantillonner cette diversité est limitée. De plus, les sondés changent au fil du temps et s’influencent mutuellement, ce qui rend la situation encore plus compliquée. La météorologie est quelque peu similaire car ses phénomènes seraient plus faciles à prévoir, du moins statistiquement, s’ils présentaient le caractère aléatoire élémentaire de la pièce de monnaie.
Examinons maintenant brièvement la notion de causalité, car c’est une façon d’aborder l’aléatoire. Bien sûr, la question de la causalité a une longue histoire que nous ne cherchons pas à développer. Signalons que le terme utilisé par Aristote (aition) et le latin (causa) trouvent leurs racines dans le vocabulaire juridique. Tout comme la responsabilité, les causes sont des moyens de comprendre pourquoi une chose se produit et quels sont les objets impliqués dans sa réalisation. Au fil du temps, la perspective a considérablement changé. Avec Leibniz, Descartes et Galilée, la causalité a été explicitée par les mathématiques, et ces mathématiques étaient dotées d’une signification théologique. En ce sens, il n’y avait pas de place pour le hasard en matière de causalité.
Dans le même ordre d’idées, Einstein a ultérieurement déclaré que "Dieu ne joue pas aux dés". L’ombre de la théologie plane toujours de manière significative sur la physique et la philosophie (et aujourd’hui sur l’informatiques) ; en même temps, une vision purement utilitaire et typiquement computationnelle de la science émerge, où la compréhension n’a plus vraiment d’importance.1 Entre Charybde et Scilla, nous soutenons que la science se rencontre là où le travail théorique a lieu (entre autres choses). Les théories ne sont pas simplement une description de la nature ; elles intègrent diverses considérations, mathématiques, empiriques, épistémologiques et méthodologiques.2 La théorisation est donc la tentative la plus aboutie de comprendre le monde scientifiquement (du moins pour une catégorie de phénomènes). Bien sûr, alors, une autre lecture de la causalité est possible, la causalité est relative à une théorie, et elle décrit ce qui se passe quand quelque chose se passe — tandis que la théorie pose par ailleurs ce qui a lieu quand rien ne se passe, comme dans le cas du principe d’inertie.
En suivant cette voie, la théorie définit l’aléatoire, s’il existe, par rapport à la causalité. La mécanique classique ne l’autorise pas (en raison du théorème de Cauchy-Lipshitz qui stipule que les forces déterminent les trajectoires), tandis que la mécanique quantique possède une forme spécifique d’aléa associée à la mesure. Globalement, nous appelons structure de détermination ce qu’une théorie dit des phénomènes et de leur relation (et cette structure peut être déterministe ou aléatoire de diverses manières).
Les théories ne sont pas seulement pertinentes pour l’aléatoire par rapport à la causalité. Premièrement, une approche presque entièrement empirique peut évaluer les probabilités, comme dans les transactions financières. Toutefois, il est toujours possible que les phénomènes s’en écartent considérablement. En revanche, les probabilités peuvent découler d’une théorie, auquel cas elles s’accompagnent d’une compréhension des phénomènes et sont plus robustes, nous reviendrons sur ce point. Deuxièmement, les résultats négatifs, comme l’imprévisibilité, sont notoirement difficiles à prouver. Pour prouver que quelque chose est impossible, nous devons avoir une façon précise de parler de ce qui est possible — sinon, l’imprévisibilité peut être seulement une propriété d’une approche particulière et disparaître dans une autre. Encore une fois, les théories sont alors le niveau approprié où l’imprévisibilité peut être fondée.
2 Comment le hasard est devenu la source des êtres vivants actuels
Dans l’étude des êtres vivants, un enjeu fondamental est la compréhension de comment les parties d’un animal, d’un organisme ou d’un écosystème semblent si bien s’articuler. Dans la théologie naturelle, l’ordre du monde vivant résulte d’un créateur divin. La théologie était utilisée pour expliquer pourquoi les êtres vivants existent même si leurs organisations et leurs arrangements dans l’"économie de la nature" ne semblent pas résulter du seul hasard. Par exemple, J. Biberg, un disciple de Linné, affirmait que "l’économie de la nature signifie la très sage disposition des êtres naturels, instituée par le créateur souverain, selon laquelle ils tendent à des fins communes et ont des fonctions réciproques".3 Dans le même ordre d’idées, William Paley, l’un des derniers partisans de la théologie naturelle, a introduit une comparaison devenue célèbre entre une pierre et une montre. Nous pouvons comprendre la pierre en affirmant qu’elle a toujours été la même ; cependant, dans le cas de la montre, les pièces dépendent les unes des autres pour atteindre une fin, et cet arrangement doit être expliqué par un horloger — et pour les vivants, Dieu serait cette explication.4 La position critique de Kant conduit à des affirmations plus modestes ; pour lui, la relation entre les parties et l’organisme ne peut être traitée par la raison pure. Elle requiert plutôt un but naturel, et ce dernier est une question de jugement.5 Cependant, la perspective de Kant ne concerne réellement que le fonctionnement des organismes, et la tradition téléomécaniste qui a suivi s’est concentrée sur ces questions, en termes modernes, la physiologie et le développement.6 Cependant, cette tradition n’aborde pas la question de comment ces organisations biologiques sont apparus.
Comme alternative à la théologie naturelle, Lamarck, entre autres, a développé une vision transformiste de la biologie. Dans un sens, sa perspective est principalement déterministe ; les caractères sont transformés lorsqu’ils accomplissent des activités et ils sont alors hérités par la génération suivante. Néanmoins, selon lui, la diversification résulte des circonstances changeantes que rencontrent les êtres vivants. En ce sens, l’aléatoire est à l’origine de la diversité biologique, en suivant une conception classique de l’aléatoire comme confluence de chaînes causales indépendantes, nous y reviendrons.
Darwin a introduit un nouveau raisonnement en s’appuyant sur la sélection artificielle. A propos de cette dernière, il écrit : "La nature donne des variations successives ; l’homme les additionne dans certaines directions qui lui sont utiles. En ce sens, on peut dire qu’il fabrique pour lui-même des races utiles".7 Des variations héritables apparaissent dans la nature, et certaines d’entre elles sont préservées parce qu’elles entraînent des conséquences favorables. Au fil du temps, "les formes infinies les plus belles et les plus merveilleuses ont évolué et évoluent encore". À chaque étape, des variations apparaissent alors que la sélection naturelle ne concerne que la préservation de certaines d’entre elles, comme le souligne une partie du sous-titre de l’Origin of species : “la préservation des races favorisées dans l’évolution” (nous soulignons, suivant Lecointre8). Cependant, la nature de ces variations et le caractère aléatoire correspondant (Darwin parle de hasard) ne sont que vaguement précisés malgré les efforts de Darwin pour synthétiser la littérature disponible au moment où il écrit.
Soulignons trois aspects de la conception de Darwin. Premièrement, certaines variations apparaissent indépendamment de leurs conséquences sur le succès reproductif des organismes, donc de leur éventuel rôle fonctionnel. Contrairement aux caractères acquis par le maintien d’une activité, cette déconnexion rejoint la notion classique de hasard évoquée plus haut, bien qu’à un niveau différent. Deuxièmement, Darwin se soucie profondément de possibles lois de la variation, et son esquisse sur le sujet laisse entrevoir un programme de recherche bien moins réductionniste que les travaux de nombre de ses successeurs. Par exemple, il met l’accent sur les variations corrélées, qui n’ont de sens qu’au niveau des organismes. Enfin, les idées de Darwin ne se limitent pas à la sélection naturelle. Il a systématisé le concept selon lequel les objets biologiques font partie d’un processus historique : l’évolution. Il a ensuite proposé de classer les êtres vivants en fonction de leur généalogie, une idée qui ne s’est concrétisée que dans la seconde partie du XXème siècle :.9
La génétique et la révolution de la biologie moléculaire ont introduit une spécification du caractère aléatoire introduit par Darwin sous forme de mutations de l’ADN, tandis que les organismes eux-mêmes étaient considérés en termes déterministes10 - vaguement importés de l’informatique.11 Alors la variation découle du hasard spécifié comme un processus moléculaire, selon la nature probabiliste des processus décrits par la thermochimie, par exemple. Ici, le caractère aléatoire des variations découle non seulement de lignes causales indépendantes qui se rencontrent, mais aussi du désordre moléculaire, au sens de Boltzmann. Les mutations modifient l’ADN de façon aléatoire, entraînant des variations phénotypiques déterminées par le nouveau "programme". Cependant, le lien entre l’ADN et le phénotype était et reste mal défini ; le concept de programme informatique n’est qu’une métaphore ad hoc pour affirmer que l’ADN détermine le phénotype et, donc, que la recherche doit se concentrer sur la manière dont la causalité va de l’ADN au phénotype. Ainsi, dans la pratique de la biologie moléculaire, au niveau des organismes, l’ADN agirait un peu comme le moteur immobile d’Aristote, mais au plan des formes, imposant ainsi des normes issues de l’histoire et définissant une téléonomie.
Soulignons que, concernant les variations, la perspective de Darwin s’intéresse principalement aux propriétés des êtres vivants, telles que leur forme ou leurs comportements. En revanche, la génétique classique ne fait qu’expliciter la structure de l’hérédité parmi les variantes héritables préexistantes et, en biologie moléculaire, les mutations ne concernent que les changements dans les séquences d’ADN qui peuvent être assez directement liés à des changements dans les protéines. Cette description est très éloignée des phénotypes à part entière. Les biologistes comblent généralement ce fossé par l’observation empirique (un changement dans une séquence d’ADN est associé à un changement dans le phénotype observé). Lorsqu’ils rédigent des modèles, comme en génétique des populations, ils supposent une relation mathématique par laquelle les génotypes déterminent les phénotypes.
En d’autres termes, la synthèse moderne et la biologie moléculaire ont considérablement contribué à la biologie en mettant l’accent sur des composantes essentielles de l’hérédité biologique et, plus précisément, sur les variations héréditaires ; cependant, elles n’ont certainement pas fourni un cadre théorique permettant de comprendre les variations biologiques et donc les chances sur lesquelles la sélection naturelle peut opérer. En particulier, la notion de mutations de l’ADN n’implique pas la possibilité d’une évolution ouverte. À titre d’illustration, les propriétés des mutations moléculaires sont simples à simuler par ordinateur ; cependant, la simulation d’un phénomène tel que l’évolution ouverte est un défi majeur pour les informaticiens.12
Prenons l’exemple de la génétique des populations théorique pour clarifier la relation entre sélection naturelle et variation. Dans ce domaine, les variants sont définis par leurs génotypes, et les modélisateurs postulent une relation mathématique entre les variants et leur fitness, c’est-à-dire le nombre statistique de leurs descendants parvenant à se reproduire. L’objectif épistémique le plus fondamental de ces modèles est de montrer que la sélection naturelle conduit effectivement à la diffusion de certains gènes dans la population, ce qui conduit à un plus grand nombre de descendants, établissant ainsi des caractères favorables que les variations aléatoires et héritables fournissent. Cependant, nous insistons sur le fait que les variations phénotypiques correspondant aux différents allèles sont postulées. Dans des situations usuelles, leur description se limite à leurs conséquences sur la valeur adaptative, ainsi le même modèle s’applique à la forme des dents ou à une enzyme digestive, par exemple. La sélection naturelle concerne principalement, comme nous l’avons souligné, la préservation de certains variants.
Néanmoins, ces modèles peuvent conduire à optimiser un caractère pour une fonction préexistante lorsqu’ils sont considérés dans le temps. Par exemple, si un caractère possède une propriété quantitative qui peut être optimisée, comme la taille des dents, alors des itérations de variation et de sélection peuvent aboutir à cette configuration singulière. De tels processus sont locaux puisque ce rôle " créatif " de la sélection naturelle n’opère que pour des fonctions et des formes dont la propriété est supposée être prédéfinie et qui sont déjà actuel. En effet, la sélection naturelle n’opère dans une direction spécifique pour certains gènes qu’à partir du moment où leurs variations ont des conséquences sur une fonction spécifique, affectant ainsi la viabilité. On retrouve ici le lien profond entre l’optimisation mathématique et telos — un lien que, d’ailleurs, les plateformes numériques actuelles exploitent lorsqu’elles conçoivent des algorithmes pour atteindre leurs objectifs. Lorsque Dawkins illustre la sélection naturelle à l’aide d’un modèle très simple, la question se pose à nouveau : il postule une configuration optimale et montre que la population converge vers elle. Puis il prend de la distance par rapport à ce modèle, arguant que "la vie n’est pas comme ça" ; cependant, il ne fournit pas de meilleur schéma, où la cible lointaine ne préexisterait pas en tant que cible dans le modèle.13 Nous pouvons alors conclure que la sélection naturelle consiste à préserver et à optimiser les fonctions préexistantes, et non leur apparition.
En d’autres termes, le schéma néo-darwinien comprend l’évolution comme une accumulation de variations issues du hasard génétique (mutations aléatoires) ; cependant, il ne fournit pas de compte rendu théorique précis de l’aspect organisationnel de ces variations. Par conséquent, il manque toujours un concept précis pour aborder les variations biologiques et le caractère aléatoire associé. La section suivante compare la situation biologique avec les concepts d’aléatoire en physique et souligne l’originalité des défis théoriques et épistémologiques de la biologie. Pour illustrer les conséquences pratiques de cette perspective, nous esquissons une nouvelle méthode pour prédire certaines variations. Enfin, nous analysons comment les organisations soutiennent activement les possibilités biologiques et comment leur disruption les conduit à s’effondrer.
3 Vers le hasard comme apparition de nouveaux possibles
Introduisons d’abord quelques remarques sur l’aléatoire en physique avant de revenir à la biologie. L’aléatoire peut être défini comme imprévisibilité dans la théorie considérée.14 Une caractéristique de la physique est que ses théories, ses modèles et son épistémologie globale supposent un espace des possibilités prédéfini. Il s’ensuit que l’aléatoire concerne l’état des objets, c’est-à-dire leur position dans l’espace abstrait prédéfini des possibilités. Alors que les cadres déterministes doivent singulariser la trajectoire que suit mathématiquement un objet, notamment ses états futurs, les cadres aléatoires posent une symétrie entre différents états afin qu’ils puissent se produire de manière égale ou commensurable.
Dans l’exemple simple du dé, les possibilités sont données par les facettes du dé qui sont supposées être symétriques — à condition que le dé ne soient pas truqué. Bien sûr, dans cet exemple, la symétrie ne concerne pas seulement les propriétés du dé ; elle correspond aussi à la dynamique du lancer. Cette dernière est suffisamment sensible aux détails pour que le résultat ne puisse pas être prédit par les joueurs (ou les physiciens), et les rotations du dé établissent l’équivalence entre ses facettes.15 Notamment, d’autres possibilités, comme un dé cassé, sont généralement exclues des discussions probabilistes. Les physiciens n’oublient pas totalement ces possibilités ; cependant, elles ne sont pas équivalentes aux autres, elles sont rares et leurs fréquences dépendent du contexte ; par conséquent, il n’est pas simple de la prendre en compte.
Les physiciens ont introduit plusieurs concepts d’aléatoire :.16 Malgré leur diversité, ils s’appuient tous sur le raisonnement exposé ci-dessus, à savoir une certaine forme de symétrie entre différentes possibilités prédéfinies. Par cette symétrie, ils définissent une métrique de l’aléatoire, appelée probabilités, qui détermine les statistiques attendues du phénomène d’intérêt lorsqu’il peut être itéré. Dans la théorie de Kolmogorov, la théorie habituelle actuelle des probabilités, et dans les cadres quantiques, un événement rompt cette symétrie pour entraîner un résultat particulier. Il est essentiel que de tels événements aléatoires "ajoutent" quelque chose à la description mathématique d’un phénomène, la singularisation d’un résultat parmi plusieurs possibilités. En ce sens, il existe un lien entre l’aléatoire et la nouveauté.
La représentation de l’aléa biologique sous forme de mutation au niveau moléculaire suit directement la physique (ou les jeux de dés). À première vue, une substitution de nucléotides semble être un processus chimique aléatoire avec des probabilités fixes. Cependant, même à ce niveau moléculaire, la situation théorique n’est pas aussi simple. La fréquence des mutations dépend des enzymes correctrices et de leur inhibition contextuelle due aux processus évolutifs.17 En d’autres termes, les symétries biologiques ne sont pas robustes et, par conséquent, les probabilités sont contextuelles.
Comme nous l’avons souligné dans l’introduction, le cœur du hasard biologique est la définition des variations comprises au-delà des aspects moléculaires des mutations. Présentons alors notre point de vue sur la biologie théorique. Contrairement aux théories de la physique, la biologie concerne principalement des objets historiques. En particulier, nous soutenons, avec d’autres, qu’un cadre théorique approprié pour la biologie, et singulièrement pour les variations biologiques, devrait tenir compte de l’évolution des espaces de possibilités.18 Notons qu’ici, changer les possibilités ne signifie pas simplement ajouter "plus du même", mais plutôt des possibilités dotées de propriétés et, donc, de relations différentes.
Même s’il est raisonnablement simple d’implémenter ce genre de schéma mathématiquement et informatiquement,19 ce n’est pas du tout la même chose de l’implémenter théoriquement et épistémologiquement. En effet, la méthode théorique de la physique consiste d’abord à postuler ce qui est possible et ensuite à déterminer ce qui va se passer. Cette caractéristique va de pair avec sa structure hypothético-déductive. Alors, en physique, la validité des hypothèses concernant l’espace des possibilités est justifiée en prédisant théoriquement et empiriquement certains aspects du phénomène envisagé. Les modèles mathématiques visant à introduire de nouvelles possibilités reviennent généralement à la méthode de la physique en rendant ces nouvelles possibilités explicites avant qu’elles ne deviennent réelles dans le modèle. En ce sens, les modélisateurs supposent, pour des raisons méthodologiques, que les nouveaux possibles préexistent en tant que virtualité avant d’apparaître ou, en termes épistémologiques, que les nouveaux possibles peuvent être connues avant d’avoir une quelconque actualité. Cependant, du point de vue des phénomènes réels qui nous intéressent, ces hypothèses sont entièrement arbitraires et les modèles restent des modèles spéculatifs pour la même raison méthodologique.
Une nouvelle épistémologie est nécessaire pour sortir de cette impasse. Dans notre travail, nous soutenons qu’au lieu d’expliquer les changements par l’invariance, comme en physique, la biologie nécessite de poser d’abord le changement et ensuite d’expliquer l’invariance locale. Nous appelons de tels invariants locaux constraintes et retravaillons l’autopoïèse, les systèmes de Rosen et les cycles travail-contraintes de Kauffman en tant que clôture entre contraintes, par lesquels les contraintes d’un organisme contribuent mutuellement à se soutenir mutuellement en canalisant les processus de transformation.20 Cependant, les contraintes jouent un autre type de rôle causal puisqu’elles permettent également l’apparition de nouvelles contraintes.21 Par exemple, les mâchoires articulées ont permis l’apparition de toutes sortes de dents. L’"enablement" s’accompagne d’un fort degré d’imprévisibilité et donc d’aléatoire, puisque la nature même de ce qui peut apparaître est non seulement inconnaissable mais aussi non-préexprimable, c’est-à-dire que nous ne pouvons pas en dresser la liste.
Néanmoins, nous soutenons que l’"enablement" fait partie du genre causal et est caractéristique de la causalité des processus véritablement historiques. Il peut sembler être un concept essentiellement négatif ; cependant, les résultats négatifs en mathématiques ou en sciences naturelles ouvrent souvent de nouvelles voies théoriques lorsque nous choisissons de nous appuyer sur eux au lieu de maintenir les approches préexistantes par une forme de déni.22 Tout d’abord, l’"enablement" peut être étudié de manière rétrospective. Par exemple, la classification phylogénétique des êtres vivants s’appuie sur l’émergence passée de nouveautés, spécifiquement des nouveautés partagées par une lignée, pour évaluer les généalogies.23 Deuxièmement, elle soulève la question de savoir ce que nous pouvons prédire de ces nouvelles possibilités et en quel sens de prédire. L’idée que les nouvelles contraintes sont globalement imprédictibles ne signifie pas qu’aucune d’entre elles ne peut être préétablie. Pour cela, de nouvelles méthodes doivent être conçues avec une épistémologie appropriée et contrôlée.
4 Une nouvelle méthode s’appuyant sur la variation biologique
Nous allons donner un exemple d’une méthode que nous développons dans ce sens. Cette méthode est la déconstruction de modèles mathématiques ; elle rappelle un peu la déconstruction chez Heidegger et Derrida, mais ses enjeux sont très différents. L’idée est de considérer un modèle ou une structure mathématique biologiquement pertinente et de le déconstruire, hypothèse par hypothèse, en recherchant à chaque étape la signification biologique possible de la négation de l’hypothèse considérée. D’un point de vue théorique, les régularités qui nous permettent de définir un modèle mathématique sont des contraintes, et elles peuvent changer, suivant ce que nous avons appelé le principe de variation.24 En déconstruisant l’objet mathématique, nous explorons certaines de ces variations — celles qui ne nécessitent pas d’hypothèses supplémentaires. Ces variations peuvent se rencontrer chez des espèces différentes, plus ou moins proches, ou être dues à la variabilité dans une même espèce.
Donnons un exemple simple de la démarche de déconstruction d’une structure mathématique biologiquement pertinente et, plus précisément, d’une forme mathématique utilisée pour décrire des caractéristiques anatomiques. La structure épithéliale des glandes mammaires du rat est généralement décrite mathématiquement comme un arbre (axiomatisé mathématiquement comme un graphe acyclique et connexe). La négation des hypothèses construisant l’arbre en mathématique conduit à :
| Hypothèse et négation | |
| Acyclique | Existence d’une boucle (en rouge) |
| connexe | Présence d’une partie détachée |
| du conduit principal (en bleu) | |
| Composé de nœuds et d’arêtes (graphe) | Présence de connexions ambiguës |
| (jonction d’épithéliums mais | |
| pas de lumières) | |
| Composé de nœuds et d’arêtes (graphique) | Pas d’arête définie (tumeur) |
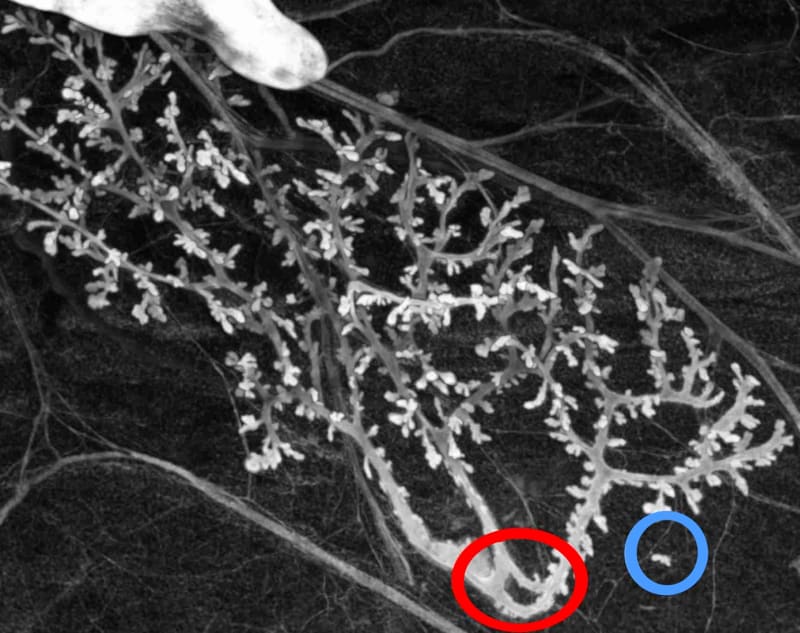
Dans le cadre d’une seule expérience, nous disposons de preuves empiriques démontrant la pertinence biologique de chaque prédiction de la déconstruction, à l’exception toutefois de la dernière, les tumeurs, dont l’existence est bien connue par ailleurs. La figure 1 illustre deux de ces prédictions. Dans chaque cas, les variations ont des conséquences sur l’utilisation des arbres pour représenter l’objet biologique, et certaines quantités caractérisant les arbres deviennent mal définies. Il ne s’agit pas ici de dire que l’objet biologique est plus complexe que sa représentation mathématique, mais de dire que les variations biologiques peuvent échapper aux cadres mathématiques utilisés pour les représenter, pour des raisons de principe. Cette affirmation n’est pas seulement un résultat négatif mais nous permet d’introduire de nouveaux raisonnements pour faire de nouvelles prédictions. Plus précisément, la méthode ci-dessus vise à préétablir certaines variations plausibles au niveau d’un individu. Elles sont plausibles car elles sont proches de situations existantes et observées. Cette notion s’apparente aux possibilités adjacentes discutées par Kauffman25 ; cependant, son utilisation technique est très différente puisqu’elle ne suppose pas de virtualités prédéfinies et vise plutôt à en trouver certaines. La méthode ne montre pas que les variations plausibles sont pour autant possibles ; une discussion biologique supplémentaire serait nécessaire pour augmenter leur plausibilité et, finalement, des observations sont nécessaires pour montrer une possibilité réelle (ce que nous fournissons dans notre exemple).
5 Aspects généraux des nouveaux possibles en biologie
Revenons à présent sur la notion générale de nouveaux possibles en biologie, en tant que composante fondamentale et aléatoire des variations.26 Pour définir précisément cette notion, précisons d’abord ce qu’est une possibilité de notre point de vue. Nous cherchons à nous éloigner de l’essentialisation des possibles et des espaces des possibles, c’est-à-dire à prendre les espaces et tous leurs points comme des choses qui existeraient par elles-mêmes. Par exemple, dans le cas simple de la position d’un objet sur une ligne droite, les possibles mathématiques sont insondables, et presque toutes les positions individuelles sont ineffables (il y a infiniment plus de nombres réels que de définitions de nombres réels individuels car les premiers sont indénombrables alors que les seconds sont dénombrables). Cependant, cette situation n’est pas véritablement un problème pour la physique car les mathématiciens et les physiciens peuvent comprendre toutes ces positions collectivement, par exemple, par une variable générique (souvent ) et une équation différentielle qui garde la même forme pour toutes les positions individuelles — ces dernières ne sont pas explicitées car le raisonnement opère sur des variables génériques.
En général, nous soutenons que les possibles véritables pour un système sont des configurations pour lesquelles la détermination du système est explicite, et en physique, elle est typiquement effectuée par un raisonnement générique. Par exemple, la chute libre est un possible explicite car la trajectoire est essentiellement la même pour toutes les positions (elles suivent la même équation). De même, un état d’équilibre thermodynamique est bien défini parce que les propriétés macroscopiques qui déterminent le système, comme la température ou la pression, sont génériques. Dans le même ordre d’idées, les séquences d’ADN ont des propriétés chimiques génériques, certaines séquences pouvant être plus stables que d’autres, et, en ce sens, elles définissent des possibles chimiques.
Cependant, les séquences d’ADN ne définissent pas les possibles biologiques car nous observons une diversité d’organisations biologiques associées. En effet, pour être une véritable possibilité, une configuration biologique doit faire partie d’une organisation qui la soutient. Les organisations déterminent la capacité d’un être vivant à perdurer dans le temps et déterminent donc, entre autres, le sort de ces séquences d’ADN. Les séquences d’ADN sont des possibilités locales, combinatoires (ici chimiques) ; nous les appelons pré-possibilités car elles peuvent être associées ou non à des possibilités biologiques, c’est-à-dire à des organisations viables dans un contexte donné. En ce sens, la méthode esquissée ci-dessus vise à trouver des pré-possibilités qui sont des possibles plausibles en effet réalisées empiriquement.
Ensuite, les nouveaux possibles sont des résultats qui ne suivent pas une détermination générique donnée par la description initiale, et a fortiori ne sont pas des résultats génériques. Donnons un exemple pour montrer pourquoi cette définition est nécessaire. Nous pouvons mathématiser la trajectoire générée par des mutations neutres de l’ADN (mutations sans conséquences fonctionnelles) par un processus de marche aléatoire. Ce processus conduit à un résultat non générique (une séquence singulière) ; cependant, le processus de marche aléatoire est le même quelle que soit la séquence spécifique. Il n’est donc pas associé à l’apparition de nouvelles possibilités. En revanche, si des séquences spécifiques conduisaient à des changements dans le processus de marche aléatoire, avec l’apparition de chromosomes, de reproductions sexuelles, etc., alors elles seraient associées des changements dans les possibles matérialisés par de nouvelles quantités requises pour décrire ces caractéristiques.
Nous soulignons que nous nous concentrons sur les relations causales, au sens large du terme, plutôt que sur l’espace des possibilités en tant qu’objet mathématique. La raison de cette position est que, d’un point de vue épistémologique, l’espace de description d’un objet et la description de sa détermination causale sont entrelacés et mutuellement dépendants, comme illustré ci-dessus. La clé des nouvelles possibilités est de savoir si une description générique est suffisante ou non pour comprendre le phénomène. L’espace mathématique peut changer sans l’apparition d’une nouvelle possibilité au sens fort. Par exemple, une pièce échange des particules avec son environnement, ce qui entraîne l’apparition de quantités supplémentaires pour décrire leurs positions et leurs vitesses. Cependant, ce processus ne représente pas de véritables nouvelles possibilités car les particules qui peuvent entrer sont du même type que celles déjà présentes dans le système et, par conséquent, les mêmes équations les décrivent : une description générique suffit à les subsumer. En revanche, les molécules biologiques peuvent faire des choses très diverses, des enzymes aux hormones ou aux moteurs moléculaires .
Prenons un peu de recul par rapport à ces aspects un peu techniques. Les possibilités en biologie sont rendue possibles ("enabled") diachroniquement par les contraintes, mais elles sont aussi générées synchroniquement par celles-ci. Par exemple, les os d’un bras génèrent la possibilité de ses différentes positions et ont permis l’apparition de diverses griffes ainsi que d’outils humains — la différence entre la génération et l’"enablement" étant l’ouverture de nouvelles possibilités dans ce dernier cas. De plus, comme mentionné ci-dessus, les contraintes biologiques font partie d’une organisation qui les maintient et qu’elles contribuent à maintenir, par exemple, par le concept de clôture entre contraintes. Notez que ce concept ne signifie pas que les organisations sont statiques. Au contraire, l’"enablement" peut avoir lieu au niveau d’un individu. De plus, certaines contraintes, appelées contraintes propulsives, ne contribuent aux organisations qu’en permettant l’apparition de nouvelles contraintes.27 Par exemple, le mécanisme mutateur chez les bactéries les conduit à connaître davantage de mutations en cas de stress, entraînant ainsi une éventuelle mutation bénéfique en réponse à ce stress mais sans spécificité dans les mutations provoquées par ce mécanisme. Si nous passons du langage des contraintes à celui des possibilités, ce cadre implique que les possibilités, en biologie, sont activement soutenues par les organisations. Dans la dernière partie de ce chapitre, nous verrons que cela implique que les possibles peuvent également s’effondrer lorsque les organisations sont disrompues.
6 Comment le hasard fait s’effondrer la diversité biologique
En un mot, les possibilités biologiques apparaissent au fil du temps et sont activement soutenues. Il est essentiel pour la suite de la discussion que ce que nous appelons les nouveaux possibles soient singuliers ou, en un sens, spécifiques, par opposition aux situations génériques. Les possibilités biologiques sont des configurations spéciales (parmi les pré-possibilités), et leur spécificité correspond à la nature de leur contribution à une organisation. Par exemple, une enzyme peut remplir une fonction parce qu’elle possède une séquence spécifique.
Remarquons maintenant que, dans la littérature scientifique récente, le terme " disruption " est un mot-clé de plus en plus utilisé pour décrire l’impact néfaste des activités humaines sur les organisations biologiques. Nous sommes en train de conceptualiser cette notion, et nous postulons qu’un aspect essentiel des disruptions en biologie est la randomisation des configurations spécifiques qui découlent de l’histoire et qui sont aussi des contributions spécifiques aux organisations.28
Fournissons deux exemples. Tout d’abord, considérons des écosystèmes où les plantes à fleurs et les pollinisateurs sont mutuellement dépendants. Leurs interactions nécessitent la synchronisation saisonnière de leur activité d’alimentation et de floraison, respectivement, afin que les plantes se reproduisent sexuellement et que les pollinisateurs ne meurent pas de faim. Il s’ensuit que les écosystèmes se trouvent dans une configuration singulière pour les périodes d’activité. Cependant, les différentes espèces utilisent différents indices pour démarrer leur activité, et ces indices sont affectés différemment par le changement climatique. Il s’ensuit que le changement climatique randomise les périodes d’activité, et puisque la situation initiale, singulière, est la condition de possibilité pour que les différentes espèces se maintiennent les unes les autres dans l’écosystème, certaines espèces sont en danger ou même disparaissent.29 Dans ce processus, une partie de l’espace des possibilités, ici les périodes d’activité des différentes espèces, s’effondre ; les dimensions de l’espace décrivant les espèces perdues disparaissent.
Un deuxième exemple est donné par les perturbateurs endocriniens, qui est une situation similaire, bien que plus complexe. Des quantités spécifiques d’hormones à des moments précis du développement sont cruciales pour canaliser les processus de développement de la différenciation cellulaire, de la morphogenèse et de l’organogenèse conduisant à des adultes viables et fertiles.30 Les perturbateurs endocriniens randomisent l’action des hormones, donc le processus de développement issu de l’évolution. Ces perturbations entraînent une diminution des fonctions, comme la baisse du QI, l’obésité, la fertilité ou le cancer.
Que signifie cette randomisation ? Les contraintes existantes définissent des pré-possibilités, par exemple, toutes les périodes d’activité possibles pour les espèces d’un écosystème ; cependant, seule une infime partie d’entre elles sont de véritables possibilités en raison de l’interdépendance des espèces. La randomisation consiste à passer du domaine étroit des pré-possibilités qui sont des possibilités (c’est-à-dire conformes à leurs propres conditions de possibilité) à un domaine plus vaste, où une partie de l’espace des possibilités n’est plus soutenue et disparaît donc. Cette randomisation est à la fois une interprétation et une spécification supplémentaire de ce que Bernard Stiegler a appelé l’augmentation de l’entropie biologique.31 En suivant le schéma de Boltzman, la randomisation en tant qu’augmentation de l’entropie signifie passer d’une partie d’un espace aux propriétés spécifiques à des propriétés plus génériques. En biologie, cependant, les propriétés spécifiques résultent de l’histoire et vont avec la viabilité. Ainsi, ce processus est principalement préjudiciable.
En un sens, les mutations sont également un processus de ce type ; la plupart sont neutres, d’autres sont préjudiciables et quelques-unes contribuent aux fonctions. Les mutations illustrent l’idée suivant laquelle les nouvelles possibilités nécessitent une exploration des pré-possibilités, déstabilisant ainsi les organisations biologiques, trouvant ainsi quelques possibilités parmi elles. Enfin, les mutations apparaissent à un rythme suffisamment lent pour ne pas déstabiliser les populations, et les conséquences des mutations néfastes sont limitées par la sélection naturelle. Si les mutations étaient plus rapides qu’elles ne le sont, elles empêcheraient le rôle de l’ADN dans l’hérédité.
L’analyse des disruptions n’est pas spécifique à celles d’origine anthropique, mais la caractéristique de l’époque actuelle est l’accélération et l’accumulation des disruptions. De nombreux êtres vivants, espèces ou écosystèmes ne peuvent y répondre en générant de nouvelles possibilités suffisamment rapidement pour compenser les disruptions. En d’autres termes, l’Anthropocène est, dans une large mesure, une course entre la randomisation destructrice des pré-possibilités biologiques existantes et l’apparition de nouvelles possibilités aléatoires, à tous les niveaux de l’organisation biologique.
Remerciements
Ce travail a été financé par la Fondation Cogito, subvention 19-111-R.
Références
- Adams, Alyssa et al. “Formal Definitions of Unbounded Evolution and Innovation Reveal Universal Mechanisms for Open-Ended Evolution in Dynamical Systems”. In: Scientific Reports 7.1 (Dec. 2017). issn: 2045-2322. doi: 10.1038/s41598-017-00810-8.
- Anderson, Chris. “The end of theory: The data deluge makes the scientific method obsolete”. In: Wired magazine 16.7 (2008), pp. 16–07. url: https://www.wired.com/2008/06/pb-theory/.
- Biberg, J. Specimen Academicum de Oeconomia Naturae. tr. fr. in Linné, L’équilibre de la nature, Vrin Paris 1972, p. 57-58. Upsala, 1749.
- Burkle, Laura A., John C. Marlin, and Tiffany M. Knight. “Plant-Pollinator Interactions over 120 Years: Loss of Species, Co-Occurrence, and Function”. In: Science 339.6127 (2013), pp. 1611–1615. issn: 0036-8075. doi: 10.1126/science.1232728.
- Colborn, T., F. S. vom Saal, and A. M. Soto. “Developmental effects of endocrine-disrupting chemicals in wildlife and humans”. eng. In: Environmental health perspectives 101.5 (Oct. 1993). PMC1519860[pmcid], pp. 378–384. issn: 0091-6765. doi: 10.1289/ehp.93101378.
- Darwin, Charles. On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life. London: John Murray, 1859.
- Dawkins, Richard. The blind watchmaker: Why the evidence of evolution reveals a universe without design. WW Norton & Company, 1986.
- Demeneix, Barbara. Losing Our Minds: How Environmental Pollution Impairs Human Intelligence and Mental Health. Oxford University Press, USA, 2014.
- Gatti, Roberto Cazzolla et al. “Niche emergence as an autocatalytic process in the evolution of ecosystems”. In: Journal of Theoretical Biology 454 (2018), pp. 110–117. issn: 0022-5193. doi: 10.1016/j.jtbi.2018.05.038.
- Huneman, Philippe. Understanding purpose: Kant and the philosophy of biology. Vol. 8. University Rochester Press, 2007.
- Kant, I. Critique of judgment. English translation: Pluhar, W. S., 1987. Hackett Publishing. Indianapolis. 1790. isbn: 0872200256.
- Kapitaniak, M. et al. “The three-dimensional dynamics of the die throw”. In: Chaos: An Interdisciplinary Journal of Nonlinear Science 22.4 (2012), p. 047504. doi: 10.1063/1. 4746038.
- Kauffman, S. A. At Home in the Universe: The Search for the Laws of Self-Organization and Complexity. Oxford University Press, 1995.
- Kauffman, Stuart A. A World Beyond Physics: The Emergence and Evolution of Life. New York: Oxford University Press, 2019.
- Lecointre, Guillaume. “The Boxes and their Content: What to Do with Invariants in Biology?” In: Life Sciences, Information Sciences. John Wiley & Sons, Ltd, 2018. Chap. 14, pp. 139–152. doi: 10.1002/9781119452713.ch14.
- Lecointre, Guillaume and Hervé Le Guyader. The tree of life: a phylogenetic classification. Vol. 20. Harvard University Press, 2006.
- Longo, G. and Maël Montévil. “Comparing Symmetries in Models and Simulations”. In: Springer Handbook of Model-Based Science. Ed. by M. Dorato, L. Magnani, and T. Bertolotti. Springer, May 2018, pp. 843–856. isbn: 9783319808307. doi: 10.1007/978- 3-319-30526-4.
- — Perspectives on Organisms: Biological time, symmetries and singularities. Lecture Notes in Morphogenesis. Heidelberg: Springer, Jan. 2014. isbn: 978-3-642-35937-8. doi: 10.1007/978-3-642-35938-5.
- Longo, G., Maël Montévil, and S. Kauffman. “No entailing laws, but enablement in the evolution of the biosphere”. In: Genetic and Evolutionary Computation Conference. GECCO’12. Philadelphia (PA, USA): ACM, July 2012. doi: 10.1145/2330784.2330946.
- Longo, G. et al. “Is information a proper observable for biological organization?” In: Progress in Biophysics and Molecular biology 109.3 (2012), pp. 108–114. issn: 0079-6107. doi: 10.1016/j.pbiomolbio.2012.06.004.
- Longo, Giuseppe. “Interfaces of Incompleteness”. In: Systemics of Incompleteness and Quasi-Systems. Ed. by Gianfranco Minati, Mario R. Abram, and Eliano Pessa. Cham: Springer International Publishing, 2019, pp. 3–55. isbn: 978-3-030-15277-2. doi: 10. 1007/978-3-030-15277-2_1.
- Loreto, Vittorio et al. “Dynamics on Expanding Spaces: Modeling the Emergence of Novelties”. In: Creativity and Universality in Language. Ed. by Mirko Degli Esposti, Eduardo G. Altmann, and François Pachet. Cham: Springer, 2016, pp. 59–83. isbn: 978-3-319-24403-7. doi: 10.1007/978-3-319-24403-7_5.
- Memmott, Jane et al. “Global warming and the disruption of plant–pollinator interactions”. In: Ecology Letters 10.8 (2007), pp. 710–717. doi: 10.1111/j.1461- 0248.2007.01061.x.
- Miquel, Paul-Antoine and Su-Young Hwang. “From physical to biological individuation”. In: Progress in Biophysics and Molecular Biology 122.1 (2016), pp. 51–57. issn: 0079-6107. doi: 10.1016/j.pbiomolbio.2016.07.002.
- Monod, J. Le hasard et la nécessité. Seuil, Paris, 1970.
- Montévil, M. “Computational empiricism : the reigning épistémè of the sciences”. In: Philosophy World Democracy (July 2021). url: https://www.philosophy-world-democracy.org/computational-empiricism.
- Montévil, Maël. “Disruption of biological processes in the Anthropocene: the case of phenological mismatch”. In: (submitted). url: https://hal.archives-ouvertes.fr/hal-03574022.
- — “Entropies and the Anthropocene crisis”. In: AI and society (May 2021). doi: 10. 1007/s00146-021-01221-0.
- — “Possibility spaces and the notion of novelty: from music to biology”. In: Synthese 196.11 (Nov. 2019), pp. 4555–4581. issn: 1573-0964. doi: 10.1007/s11229-017-1668-5.
- Montévil, Maël and Matteo Mossio. “Biological organisation as closure of constraints”. In: Journal of Theoretical Biology 372 (May 2015), pp. 179–191. issn: 0022-5193. doi: 10.1016/j.jtbi.2015.02.029.
- — “The Identity of Organisms in Scientific Practice: Integrating Historical and Relational Conceptions”. In: Frontiers in Physiology 11 (June 2020), p. 611. issn: 1664-042X. doi: 10.3389/fphys.2020.00611.
- Montévil, Maël et al. “Theoretical principles for biology: Variation”. In: Progress in Biophysics and Molecular Biology 122.1 (Aug. 2016), pp. 36–50. issn: 0079-6107. doi: 10.1016/j.pbiomolbio.2016.08.005.
- Paley, William. Natural Theology: or, Evidences of the Existence and Attributes of the Deity. London: J. Faulder, 1802.
- Soros, LB and Kenneth O Stanley. “Identifying necessary conditions for open-ended evolution through the artificial life world of chromaria”. In: ALIFE 14: The Fourteenth Conference on the Synthesis and Simulation of Living Systems. Vol. 14. 2014, pp. 793–800. doi: 10.7551/978-0-262-32621-6-ch128.
- Stiegler, Bernard. The neganthropocene. Open Humanites Press, 2018.
- Tenaillon, Olivier et al. “Second-order selection in bacterial evolution: selection acting on mutation and recombination rates in the course of adaptation”. In: Research in Microbiology 152.1 (2001), pp. 11–16. issn: 0923-2508. doi: 10.1016/S0923-2508(00) 01163-3.
- Walsh, D. M. “Action, program, metaphor”. In: Interdisciplinary Science Reviews 45.3 (2020), pp. 344–359. doi: 10.1080/03080188.2020.1795803
∗https://montevil.org Institut de Recherche et d’Innovation, Centre Pompidou; IHPST, Université Paris 1 and Centre Cavaillès, UAR 3608 République des Savoirs, ÉNS and CNRS.
1Chris Anderson. “The end of theory: The data deluge makes the scientific method obsolete”. In: Wired magazine 16.7 (2008), pp. 16–07. url: https://www.wired.com/2008/06/pb-theory/.
2M. Montévil. “Computational empiricism : the reigning épistémè of the sciences”. In: Philosophy World Democracy (July 2021). url: https://www.philosophy-world-democracy.org/computational-empiricism.
3J. Biberg. Specimen Academicum de Oeconomia Naturae. tr. fr. in Linné, L’équilibre de la nature, Vrin Paris 1972, p. 57-58. Upsala, 1749, p. 1.
4William Paley. Natural Theology: or, Evidences of the Existence and Attributes of the Deity. London: J. Faulder, 1802, p. 1.
5I. Kant. Critique of judgment. English translation: Pluhar, W. S., 1987. Hackett Publishing. Indianapolis. 1790. isbn: 0872200256.
6Philippe Huneman. Understanding purpose: Kant and the philosophy of biology. Vol. 8. University Rochester Press, 2007.
7Charles Darwin. On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life. London: John Murray, 1859.
8Guillaume Lecointre. “The Boxes and their Content: What to Do with Invariants in Biology?” In: Life Sciences, Information Sciences. John Wiley & Sons, Ltd, 2018. Chap. 14, pp. 139–152. doi: 10.1002/9781119452713.ch14.
9Guillaume Lecointre and Hervé Le Guyader. The tree of life: a phylogenetic classification. Vol. 20. Harvard University Press, 2006.
10J. Monod. Le hasard et la nécessité. Seuil, Paris, 1970.
11G. Longo et al. “Is information a proper observable for biological organization?” In: Progress in Biophysics and Molecular biology 109.3 (2012), pp. 108–114. issn: 0079-6107. doi: 10.1016/j.pbiomolbio.2012.06.004; D. M. Walsh. “Action, program, metaphor”. In: Interdisciplinary Science Reviews 45.3 (2020), pp. 344–359. doi: 10.1080/03080188.2020.1795803.
12LB Soros and Kenneth O Stanley. “Identifying necessary conditions for open-ended evolution through the artificial life world of chromaria”. In: ALIFE 14: The Fourteenth Conference on the Synthesis and Simulation of Living Systems. Vol. 14. 2014, pp. 793–800. doi: 10.7551/978-0-262-32621-6-ch128.
13Richard Dawkins. The blind watchmaker: Why the evidence of evolution reveals a universe without design. WW Norton & Company, 1986, p. 60.
14G. Longo and Maël Montévil. “Comparing Symmetries in Models and Simulations”. In: Springer Handbook of Model-Based Science. Ed. by M. Dorato, L. Magnani, and T. Bertolotti. Springer, May 2018, pp. 843–856. isbn: 9783319808307. doi: 10.1007/978-3-319-30526-4.
15seulement dans une certaine mesure, voir M. Kapitaniak et al. “The three-dimensional dynamics of the die throw”. In: Chaos: An Interdisciplinary Journal of Nonlinear Science 22.4 (2012), p. 047504. doi: 10.1063/1.4746038.
16voir Longo and Montévil, “Comparing Symmetries in Models and Simulations”, pour un aperçu.
17Olivier Tenaillon et al. “Second-order selection in bacterial evolution: selection acting on mutation and recombination rates in the course of adaptation”. In: Research in Microbiology 152.1 (2001), pp. 11–16. issn: 0923-2508. doi: 10.1016/S0923-2508(00)01163-3.
18G. Longo and Maël Montévil. Perspectives on Organisms: Biological time, symmetries and singularities. Lecture Notes in Morphogenesis. Heidelberg: Springer, Jan. 2014. isbn: 978-3-642-35937-8. doi: 10.1007/978-3-642-35938-5; Roberto Cazzolla Gatti et al. “Niche emergence as an autocatalytic process in the evolution of ecosystems”. In: Journal of Theoretical Biology 454 (2018), pp. 110–117. issn: 0022-5193. doi: 10.1016/j.jtbi.2018.05.038; Vittorio Loreto et al. “Dynamics on Expanding Spaces: Modeling the Emergence of Novelties”. In: Creativity and Universality in Language. Ed. by Mirko Degli Esposti, Eduardo G. Altmann, and François Pachet. Cham: Springer, 2016, pp. 59–83. isbn: 978-3-319-24403-7. doi: 10.1007/978-3-319-24403-7_5; Stuart A Kauffman. A World Beyond Physics: The Emergence and Evolution of Life. New York: Oxford University Press, 2019.
19Alyssa Adams et al. “Formal Definitions of Unbounded Evolution and Innovation Reveal Universal Mechanisms for Open-Ended Evolution in Dynamical Systems”. In: Scientific Reports 7.1 (Dec. 2017). issn: 2045-2322. doi: 10.1038/s41598-017-00810-8.
20Maël Montévil and Matteo Mossio. “Biological organisation as closure of constraints”. In: Journal of Theoretical Biology 372 (May 2015), pp. 179–191. issn: 0022-5193. doi: 10.1016/j.jtbi.2015.02.029.
21G. Longo, Maël Montévil, and S. Kauffman. “No entailing laws, but enablement in the evolution of the biosphere”. In: Genetic and Evolutionary Computation Conference. GECCO’12. Philadelphia (PA, USA): ACM, July 2012. doi: 10.1145/2330784.2330946.
22Giuseppe Longo. “Interfaces of Incompleteness”. In: Systemics of Incompleteness and Quasi-Systems. Ed. by Gianfranco Minati, Mario R. Abram, and Eliano Pessa. Cham: Springer International Publishing, 2019, pp. 3–55. isbn: 978-3-030-15277-2. doi: 10.1007/978-3-030-15277-2_1.
23Lecointre and Le Guyader, The tree of life: a phylogenetic classification.
24Maël Montévil et al. “Theoretical principles for biology: Variation”. In: Progress in Biophysics and Molecular Biology 122.1 (Aug. 2016), pp. 36–50. issn: 0079-6107. doi: 10.1016/j.pbiomolbio.2016.08.005.
25S. A. Kauffman. At Home in the Universe: The Search for the Laws of Self-Organization and Complexity. Oxford University Press, 1995.
26une discussion détaillée peut être trouvée dans Maël Montévil. “Possibility spaces and the notion of novelty: from music to biology”. In: Synthese 196.11 (Nov. 2019), pp. 4555–4581. issn: 1573-0964. doi: 10.1007/s11229-017-1668-5.
27Paul-Antoine Miquel and Su-Young Hwang. “From physical to biological individuation”. In: Progress in Biophysics and Molecular Biology 122.1 (2016), pp. 51–57. issn: 0079-6107. doi: 10.1016/j.pbiomolbio.2016.07.002; Maël Montévil and Matteo Mossio. “The Identity of Organisms in Scientific Practice: Integrating Historical and Relational Conceptions”. In: Frontiers in Physiology 11 (June 2020), p. 611. issn: 1664-042X. doi: 10.3389/fphys.2020.00611.
28Maël Montévil. “Entropies and the Anthropocene crisis”. In: AI and society (May 2021). doi: 10.1007/s00146-021-01221-0; Maël Montévil. “Disruption of biological processes in the Anthropocene: the case of phenological mismatch”. In: (submitted). url: https://hal.archives-ouvertes.fr/hal-03574022.
29Jane Memmott et al. “Global warming and the disruption of plant–pollinator interactions”. In: Ecology Letters 10.8 (2007), pp. 710–717. doi: 10.1111/j.1461-0248.2007.01061.x; Laura A. Burkle, John C. Marlin, and Tiffany M. Knight. “Plant-Pollinator Interactions over 120 Years: Loss of Species, Co-Occurrence, and Function”. In: Science 339.6127 (2013), pp. 1611–1615. issn: 0036-8075. doi: 10.1126/science.1232728.
30T. Colborn, F. S. vom Saal, and A. M. Soto. “Developmental effects of endocrine-disrupting chemicals in wildlife and humans”. eng. In: Environmental health perspectives 101.5 (Oct. 1993). PMC1519860[pmcid], pp. 378–384. issn: 0091-6765. doi: 10.1289/ehp.93101378; Barbara Demeneix. Losing Our Minds: How Environmental Pollution Impairs Human Intelligence and Mental Health. Oxford University Press, USA, 2014.
31Bernard Stiegler. The neganthropocene. Open Humanites Press, 2018.