How does randomness shape the living?
Figuring Chance: Questions of Theory
In biology, randomness is a critical notion to understand variations; however this notion is typically not conceptualized precisely. Here we provide some elements in that direction.
Abstract
Physics has several concepts of randomness that build on the idea that the possibilities are pre-given. By contrast, an increasing number of theoretical biologists attempt to introduce new possibilities, that is to say, changes of possibility space – an idea already discussed by Bergson and that was not genuinely pursued scientifically until recently (except, in a sense, in systematics, i.e, the method to classify living beings).
Then, randomness operates at the level of possibilities themselves and is the basis of the historicity of biological objects. We emphasize that this concept of randomness is not only relevant when aiming to predict the future. Instead, it shapes biological organizations and ecosystems. As an illustration, we argue that a critical issue of the Anthropocene is the disruption of the biological organizations that natural history has shaped, leading to a collapse of biological possibilities.
Table of contents
Reading time: ~40 min
How does randomness shape the living?
Abstract
Physics has several concepts of randomness that build on the idea that the possibilities are pre-given. By contrast, an increasing number of theoretical biologists attempt to introduce new possibilities, that is to say, changes of possibility space – an idea already discussed by Bergson and that was not genuinely pursued scientifically until recently (except, in a sense, in systematics, i.e, the method to classify living beings).
Then, randomness operates at the level of possibilities themselves and is the basis of the historicity of biological objects. We emphasize that this concept of randomness is not only relevant when aiming to predict the future. Instead, it shapes biological organizations and ecosystems. As an illustration, we argue that a critical issue of the Anthropocene is the disruption of the biological organizations that natural history has shaped, leading to a collapse of biological possibilities.
1 Causality and randomness
This chapter discusses how randomness became a pillar of biology and how its precise conceptualization remains a challenge for current theoretical biology, with applications to the stakes of our time, commonly called the Anthropocene. Now randomness is a complex notion in the sciences, and it is necessary for our discussion to go back briefly on its history outside biology.
Randomness is at the crossroad of different questions. First comes causality and, in a sense, a random phenomenon is not entailed by causes. Second comes betting, with money games and insurances (historically, for the trading boats during colonization) — and here computations are critical. Probability theories were developed precisely to provide metrics to randomness. Last comes the notion of unpredictability, and it is the most recent one.
In sciences, these different questions combine ... in almost every possible way. For example, so-called chaotic dynamics are deterministic, thus devoid of "causal randomness" but unpredictable. Why? These peculiar situations are due to two combining reasons. First, measurement in classical mechanics is never perfect; we assess an object’s position and velocity up to a certain precision – this is a matter of principles, not of technology. Second, however close initial conditions are, the subsequent trajectories will diverge very quickly (exponentially fast). Combining these two factors implies unpredictability; small causes, even the ones we cannot measure, can have significant effects. This situation is the so-called butterfly effect, the idea that a butterfly flapping its wings can create a hurricane elsewhere. It is also why we cannot tell whether the solar system is stable or whether a planet will be ejected from it at some point.
Let us examine another mismatch. In computer sciences, a computer is deterministic and predictable; as Turing calls it, it is a discrete state machine where access to the state can be perfect. However, randomness appears when we put different theoretical computers together (including the different cores in current computers) because there is no certainty on which computation will be faster. This randomness corresponds indeed to unpredictability, but its peculiarity is that it does not have a metric (there are no probabilities). Let us give a picturesque example of this. Imagine the simulation of wind acting on the roof so that roof tiles fall. Imagine also the simulation of the walk of a pedestrian. Then, if different cores perform these two simulations, the roof tile may or may not fall on the pedestrian because the update of both models is not synchronized (if it is poorly designed). Then, computer scientists typically design their algorithm so that it leads to the intended results in all situations.
Nevertheless, in a sense, randomness always goes with unpredictability. But, the relationship between the two different notions is not entirely straightforward. For example, the random motion of molecules leads a delicious smell to propagate in a kitchen and beyond. In general, when we study a gas, as Boltzmann puts it, the molecular chaos leads the gas to tend to the situation of maximum entropy, which is perfectly predictable. Along the same line, pure probabilistic randomness is not the most unpredictable situation. For example, the heads or tails game statistics are very well known, and we can make predictions for a large number of throws. probabilities are deeply distinct from anomia, the absence of norms or laws. it is the same in the case of quantum mechanics, where possibilities and probabilities are very well defined. By contrast, the ability of polls in an election to predict outcomes is limited at best. One reason for this is that the citizens and localities are diverse, and the ability of polls to sample this diversity is limited. Moreover, they change over time and influence each other, making the situation even more complicated. Meteorology is somewhat similar because these phenomena would be easier to predict, at least statistically, if they displayed the coin’s elementary randomness.
Now, let us examine the notion of causation briefly since it is a way to address randomness. Of course, the question of causation has a long history that we do not aim to unfold. Let us mention that the term used by Aristotle (aition) and the Latin (causa) have their roots in legal vocabulary. Like responsibility, causes are ways to understand why something happens and what objects are involved in it happening. Over time, the perspective changed significantly. With Leibniz, Descartes, and Galileo, causation was made explicit by mathematics, and these mathematics were endowed with theological meaning. In this sense, there was no room for randomness w.r. causation.
Along this line, Einstein later said that "God does not play dice". The shadow of theology still lingers significantly on physics and philosophy (and nowadays on computer sciences); on the other side, a purely utilitarian, typically computational view of science emerges where understanding does not matter genuinely anymore ( Anderson, 2008). Between Charybdis and Scilla, we argue that science lies where theoretical work is performed (among other things). Theories are not merely a description of nature; they embed various considerations, mathematical, empirical, epistemological, and methodological ( Montevil, 2021). Theorization, then, is the best effort to make sense scientifically of the world (at least of a category of phenomena). Of course, then, another reading on causation is possible, causation is relative to a theory, and it describes what happens when something happens — while the theory posits what is taking place when nothing happens, like in the in the principle of inertia.
Following this line, the theory defines randomness w.r. to causation, if any. Classical mechanics does not allow it (due to the Cauchy-Lipshitz theorem that states that forces do determine trajectories), while quantum mechanics has a specific form of randomness associated with measurement. Overall we call structure of determination what a theory says about phenomena and their relation (and this structure can be deterministic or random in diverse ways).
Now theories are not relevant only to randomness w.r. to causation. First, an almost entirely empirical approach may assess probabilities, like in financial trading. However, there is always the possibility that the phenomena depart strongly from those. By contrast, probabilities may stem from a theory, in which case they come with an understanding of the phenomena and are more robust, we will come back to this point. Second, negative results, like unpredictability, are notoriously difficult to prove. To prove that something is impossible, we need to have a precise way to talk about what is possible — otherwise, unpredictability may be only a property of a particular approach and vanish in another. Again, theories are then the proper level where unpredictability may be grounded.
2 How randomness came to originate current living beings
A primary question in the study of living beings is how we should understand that the parts of an animal, an organism, or an ecosystem seem to fit so well together. In natural theology, the order of the living world resulted from a divine creator. Theology was used to explain why living beings exist even though their organizations and arrangements in the “economy of nature” do not seem to result from chance alone. For example, J. Biberg, a disciple of Linneus, stated that “economy of nature means the very wise disposition of natural beings, instituted by the sovereign creator, according to which they tend to common ends and have reciprocal functions” ( Biberg, 1749, p. 1). Along the same line, William Paley, one of the last proponents of natural theology, famously compared a stone and a watch. We can understand the stone by stating that it has always been the same; however, in the case of the watch, the parts depend on each other to meet an end, and this arrangement needs to be explained by a watchmaker – and for the living, God would be the explanation ( Paley, 1802). Kant’s critical position leads to more modest claims; for him, the relationship between the parts and the organism cannot be addressed by pure reason. Instead, it requires a natural purpose, and the latter is a matter of judgment ( Kant, 1790). However, Kant’s perspective only really accommodates the functioning of organisms, and the subsequent teleomechanist tradition focused on these questions, in modern terms, physiology and development ( Huneman, 2007). However, this tradition does not address how these biological organizations came to be.
As an alternative to natural theology, Lamarck, among others, developed a transformist view of biology. In a sense, his perspective is primarily deterministic; characters are transformed when performing activities and are inherited by the next generation. Nevertheless, in his view, diversification results from the changing circumstances living beings meet. In this sense, randomness originates biological diversity, provided that a classical concept of randomness is the confluence of independent causal chains, we will come back to this point.
Darwin introduced a new rationale by building on artificial selection. Concerning the latter, he states, “nature gives successive variations; man adds them up in certain directions useful to him. In this sense, he may be said to make for himself useful breeds” ( Darwin, 1859). Heritable variations appear in the wild, and some of these are preserved because they lead to favorable consequences. Over time, “endless forms most beautiful and most wonderful have been, and are being, evolved.” At each step, variation appears while natural selection is only about the preservation of some of them, as emphasized by part of the subtitle of the Origin of species: “the preservation of favored races in evolution” (we emphasize, following Lecointre (2018)). However, the nature of these variations and the corresponding randomness (Darwin refers to it as chance) are only loosely specified despite Darwin’s best efforts to synthesize the literature available at the time of his writing.
Let us stress three points concerning Darwin’s view. First, some variations appear irrespective of their consequences on the reproductive success of organisms, thus of their possible functional role. In contrast with characters acquired by sustaining an activity, this disconnection meets the classical notion of randomness mentioned above, albeit at a different level. Second, Darwin cares deeply about possible laws of variation, and his sketch on the topic hints at a research program that is far less reductionist than the work of many of his successors. For example, he emphasizes correlated variations, which only make sense at the level of organisms. Last, Darwin’s insights are not limited to natural selection. He systematized the concept that biological objects are part of a historical process: evolution. Then he suggested classifying living beings based on their genealogy, an idea that only came to fruition in the second part of the XXth century ( Lecointre & Le Guyader, 2006).
Genetics and the molecular biology revolution introduced a specification for Darwin’s randomness as DNA mutations, while the organisms themselves were considered in deterministic terms (Monod, 1970) – loosely imported from computer sciences ( Longo, Miquel, et al., 2012 ; Walsh, 2020). Then variation follows from randomness specified as a molecular process, according to the probabilistic nature of the processes described by thermochemistry, for example. Here, the randomness of variations stems not only from independent causal lines that meet but also from molecular disorder, in the sense of Boltzmann. Mutations change DNA randomly, leading to phenotypic variations determined by the new “program”. However, the connection between DNA and phenotype was and remains poorly defined; the concept of computer program remains merely an ad hoc metaphor to state that DNA determines the phenotype and, thus, that research should focus on how causality goes from DNA to the phenotype. In the practice of molecular biology, thus, at the level of organisms, DNA would act somewhat like Aristotle’s unmoved mover, but at the level of forms, thus enforcing norms stemming from history (defining a kind of teleonomy).
Let us emphasize that, concerning variations, Darwin’s perspective cares mainly about the properties of living beings, such as their form or behaviors. By contrast, classical genetics only makes explicit the structure of heredity among preexisting heritable variants, and, in molecular biology, mutations are only about changes in DNA sequences that may be somewhat directly related to changes in proteins. This description is very far from full-fledged phenotypes. Biologists typically bridge this gap by empirical observation (a change in a DNA sequence is associated with a change in observed phenotype). When writing models, like in population genetics, they assume a mathematical relationship by which genotypes determine phenotypes.
In other words, modern synthesis and molecular biology contributed considerably to biology by emphasizing critical components of biological heredity and, specifically, heritable variations; however, it certainly did not provide a theoretical framework to understand biological variations and thus the chances that natural selection can operate upon. In particular, the notion of DNA mutations does not entail the possibility of open-ended evolution. As an illustration, the properties of molecular mutations are straightforward to simulate with a computer; however, simulating something like open-ended evolution is an open challenge for computer scientists ( Soros & Stanley, 2014).
Let us take the example of theoretical population genetics to clarify the relationship between natural selection and variation. In this field, variants are defined by their genotypes, and modelers postulate a mathematical relationship between variants and their fitness, i.e., their statistical number of offspring reaching reproduction. These models’ most basic epistemic aim is to show that natural selection indeed leads to the spread of the genes in the population, leading to more offspring, thus establishing favorable characters that random, heritable variations provide. However, we emphasize that the phenotypic variations corresponding to the different alleles are postulated. In typical situations, their description is limited to their consequences on fitness, so the same model applies to teeth shapes or a digestive enzyme, for example. Natural selection is primarily, as we emphasized, about the preservation of some variants.
Nevertheless, these models can lead to optimizing a character for a preexisting function when considered over time. For example, if a character has some quantitative property that may be optimized, such as the size of teeth, then iterations of variation and selection can bring about this singular configuration. Such processes are local since this "creative" role of natural selection only operates for functions and forms whose property is assumed to be pre-defined and are already actual. Indeed, natural selection operates in a specific direction for some genes only once their variations have consequences on a specific function, thus impacting viability. Here, we find the deep connection between mathematical optimization and telos — a connection that, incidentally, today’s digital platforms harness when designing algorithms to fulfill their ends. When Dawkins illustrates natural selection with a toy model, the issue appears again: he postulates an optimal configuration and shows that the population converges to it. Then he takes a distance from this model, arguing that “life isn’t like that”; however, he does not provide a better scheme, where the distant target would not preexist as a target in the model ( Dawkins, 1986, p. 60). We can then conclude that natural selection is about preserving and optimizing preexisting functions, not their appearance.
In other words, the neo-Darwinian scheme understands evolution as an accumulation of variations stemming from genetic randomness (random mutations); however, it does not provide an accurate theoretical account of the organizational aspect of these variations. Therefore, a precise concept to address biological variations and the associated randomness is still missing. This chapter compares the biological situation with concepts of randomness in physics and emphasizes the originality of biology’s theoretical and epistemological challenges. To illustrate the practical ramification of this perspective, we sketch a new method to predict some variations. Last, we analyze how organizations actively sustain biological possibilities and how their disruption leads to them collapsing.
3 Towards randomness as new possibilities
Let us first introduce some remarks on randomness in physics before going back to biology. Randomness may be defined as unpredictability in the intended theory ( Longo & Montévil, 2018). A characteristic of physics is that its theories, models, and overall epistemology assumes pre-defined possibilities. It follows that randomness is about the state of objects, that is to say, about their positions in the abstract space of pre-defined possibilities. While deterministic frameworks need to singularize the trajectory that an object follows mathematically, particularly its future states, random frameworks posit a symmetry between different states so that they can equally or commensurably occur.
In the simple example of the dice, the possibilities are given by the dice facets, which are assumed to be symmetric – provided the dice are fair. Of course, in this example, the symmetry is not just about the dice’s properties; it also corresponds to the dynamic of the throw. The latter is sensitive enough to details so that the outcome cannot be predicted by the players (or physicists), and the rotations of the dice establish the equivalence between its facets (only to an extent, see Kapitaniak et al., 2012). Notably, other possibilities like broken dice are typically excluded from probabilistic discussions. Physicists do not forget this possibility; however, it is not equivalent to the others and rare, and its frequency depends on changing circumstances; therefore, it is not straightforward to accommodate it.
Physicists have introduced several concepts of randomness (see Longo & Montévil, 2018, for an overview). Despite their diversity, they all build on the rationale discussed above, namely some form of symmetry between different pre-defined possibilities. By this symmetry, they define a metric for randomness, called probabilities, that determine the expected statistics of the phenomenon of interest when it can be iterated. In Kolmogorov, the current usual theory of probabilities, and in quantum frameworks, an event is breaking this symmetry to entail a particular outcome. It is significant that such random events "add" something to the mathematical description of a phenomenon, the singularization of one outcome among several possibilities. In this sense, there is a connection between randomness and novelty.
The account of biological randomness as molecular-level mutation follows physics (or dice games) straightforwardly. At first sight, a nucleotide substitution seems to be a random chemical process with set probabilities. However, even at this molecular level, the theoretical situation is not that simple. The frequency of mutations depends on correcting enzymes and their contextual inhibition due to evolutionary processes ( Tenaillon et al., 2001). In other words, biological symmetries are not robust and, accordingly, probabilities are contextual.
As emphasized in the introduction, the heart of biological randomness is the definition of variations beyond the molecular aspects of mutations. To this end, let us introduce our perspective on theoretical biology. Unlike in the theories of physics, biology is primarily about historical objects. In particular, we argue, with others, that a proper theoretical framework for biology, and singularly biological variations, should accommodate changing possibility spaces ( Gatti et al., 2018 ; Loreto et al., 2016). Let us note that changing possibilities here does not just mean adding “more of the same”; instead, it means possibilities endowed with different properties and, thus, relationships.
Even though it is reasonably straightforward to implement this kind of scheme mathematically and computationally ( Adams et al., 2017), it is not the same problem to implement it theoretically and epistemologically. Indeed, the theoretical method of physics is firstly to postulate was is possible and then determine what is going to happen. This feature goes with its hypothetical-deductive structure. Then, in physics, the validity of the assumptions concerning the possibility space is justified by predicting some aspects of the intended phenomenon theoretically and empirically. Mathematical models aiming to introduce new possibilities typically fall back to the physics method by making these new possibilities explicit before they become actual in the model. In this sense, modelers assume that new possibilities preexist as virtuality before they appear or, in epistemological terms, that the new possibilities can be known before they have any kind of actuality, and they do so for methodological reasons. However, from the perspective of the actual phenomena of interest, these assumptions are entirely arbitrary, and the models remain speculative toy models for the same methodological reason.
A new epistemology is required to overcome this deadlock. In my work, I argue that instead of explaining changes by invariance, like in physics, biology requires to posit change first and then to explain local invariance. My group calls such local invariants constraints and reworked autopoiesis, Rosen’s (M,R) systems, and Kauffman’s work-constraints cycles as the closure of constraints, whereby constraints of an organism mutually contribute to sustaining each other by canalyzing processes of transformation ( Montévil & Mossio, 2015). However, constraints play another kind of causal role since they also enable the appearance of new constraints ( Longo, Montévil, & Kauffman, 2012). For example, articulated jaws enabled teeth of all kinds. Enablement goes with a strong kind of unpredictability and thus of randomness since it is the very nature of what can appear that is not only unknowable but unprestatable; that is to say, we cannot list what is possible.
Nevertheless, we argue that enablement is part of the causal genra and characteristic of truly historical processes. Enablement may seem mostly a negative concept; however, negative results in mathematics or natural sciences often open new theoretical paths when we choose to build on them instead of maintaining current approaches by denial ( Longo, 2019). Firstly, enablement can be studied retrospectively. For instance, the phylogenetic classification of living beings builds on the past emergence of novelties, Specifically shared novelties, to assess genealogies ( Lecointre & Le Guyader, 2006). Second, it raises the question of what we can predict about these new possibilities and in what sense of predicting? The idea that new constraints are overall unprestatable does not mean that none of them may be pre-stated. For that, new methods should be designed with an appropriate and controlled epistemology.
4 A new method building on biological variations
Let us give an example of a method we are developing along this line. This method deconstructs mathematical models; it is somewhat reminiscent of deconstruction in Heidegger and Derrida’s work; however, its stakes are very different. The idea is to consider a model or a mathematical structure that is biologically relevant and deconstruct it, hypothesis by hypothesis, by investigating at each step the possible biological meaning of the negation of the considered hypothesis. From a theoretical perspective, the regularities enabling us to define a mathematical model are constraints, and they can change, following what we have called the principle of variation ( Montévil et al., 2016). By deconstructing the mathematical object, we explore some of these variations — the ones that do not require additional assumptions. These variations may be met in different, more or less closely related species or due to variability in the same species.
Let us give a simple example of the approach to deconstructing a biologically relevant mathematical structure and, more precisely, a mathematical form used to describe anatomical features. The epithelial structure of rat mammary glands is generally described mathematically as a tree (mathematically axiomatized as an acyclic and connex graph). The negation of the hypotheses constructing the mathematical tree structure leads to:
| Hypothesis | Negation |
| Acyclic | Existence of a loop (in red) |
| connex | Presence of a part detached |
| from the main duct (in blue) | |
| Composed of nodes and edges (graph) | Presence of ambiguous connections |
| (junction of epithelia but | |
| not lumens) | |
| Composed of nodes and edges (graph) | No defined edge (tumor) |
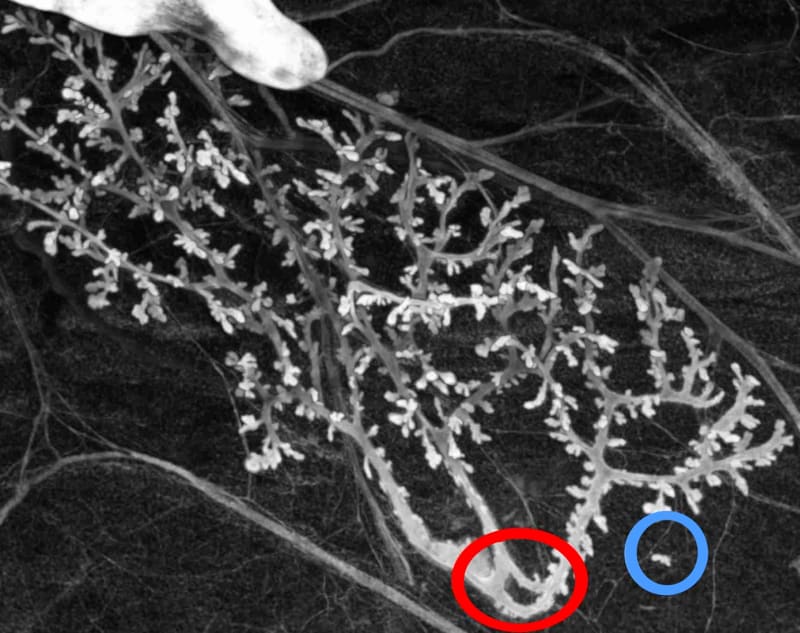
In the context of a single experiment, we have empirical evidence showing the biological relevance of all predictions of deconstruction but one. However, the latter, tumors is a well-know biological situation; therefore, it is also relevant. Figure 1 illustrates two of these predictions. In each case, the variations have consequences for using the tree structure to represent the biological object, and some quantities characterizing trees become ill-defined. The point here is not to say that the biological object is more complex than its mathematical representation but to say that the biological variations can escape the mathematical frameworks used to represent them, for principled reasons. This statement is not just a negative result but enables us to introduce new rationales to make new predictions. Specifically, the method above aims to pre-state some plausible variations at a character’s level. They are plausible since they are close to existing and observed situations. This notion is akin to the adjacent possibilities discussed by S. A. Kauffman (1995); however, its technical use is very different since it does not assume pre-defined virtualities and aims instead to find some of them. The method does not show that the plausible variations are genuinely possible; a further biological discussion would be required to increase their plausibility, and, ultimately, observations are required to show a genuine possibility (which we provide in our example).
5 General aspects of new possibilities in biology
Let us now go back to the general concept of new possibilities in biology as a fundamental, random component of variations (a detailed discussion can be found in Montévil, 2019). To define this notion precisely, let us first specify what a possibility is from our perspective. We aim to move away from the essentialization of possibilities and possibility spaces, that is to say, taking spaces and all their points as things that would exist by themselves. For example, in the simple case of the position of an object on a straight line, the mathematical possibilities are unfathomable, and almost all individual positions are ineffable (there are infinitely more real numbers than definitions of individual real numbers because the former are uncountable while the latter are countable). However, this situation is not genuinely a problem for physics because mathematicians and physicists can understand all these positions collectively, for example, by a generic variable (often x) and a differential equation that keeps the same form for all individual positions – the latter are not made explicit because the reasoning operates on generic variables.
In general, we argue that genuine possibilities for a system are configurations for which the system determination is explicit, and in physics, it is typically performed by generic reasoning. For example, free fall is an explicit possibility because the trajectory is essentially the same for all positions (they follow the same equation). Similarly, a state at thermodynamic equilibrium is well defined because its macroscopic properties determining the system, such as temperature or pressure, are generic. Along the same line, DNA sequences have generic chemical properties, where some sequences may be more stable than others, and, in this sense, they define chemical possibilities.
However, DNA sequences do not define biological possibilities because we observe a diversity of related biological organizations. Indeed, to be a genuine possibility, a biological configuration needs to be part of an organization that sustains it. Organizations determine the ability of a living being to last over time and thus, among other things, determine the fate of these DNA sequences. DNA sequences are combinatoric local possibilities (here chemical); we call them pre-possibilities as they may or may not be associated with biological possibilities, that is to say viable organizations in a given context. In this sense, the method sketched above aims to find pre-possibilities that are plausible possibilities realized empirically.
Then, new possibilities are outcomes that do not follow a generic determination given by the initial description, and a fortiori are not generic outcomes. Let us give an example to show why this definition is required. We can mathematize the trajectory generated by neutral DNA mutations (mutations with no functional consequences) by a random walk process. This process leads to a non-generic outcome (a singular sequence); however, the random walk process is the same irrespective of the specific sequence. Therefore it is not associated with the appearance of new possibilities. By contrast, if specific sequences would lead to changes in the random-walk process, with the emergence of chromosomes, sexual reproductions, etc., then it would be associated with a change in the possibilities materialized by new quantities required to describe these features.
We emphasize that we focus on causal relationships, in the broad sense of the word, instead of the space of possibility as a mathematical object. The reason for this stance is that, from an epistemological perspective, an object’s space of description and the description of its causal determination are intertwined and mutually dependent, as illustrated above. The key to new possibilities is whether or not a generic description is sufficient to understand the phenomenon. The mathematical space can change without the appearance of a new possibility in the strong sense. For example, a room exchanges particles with its surroundings, leading to supplementary quantities to describe their position and velocity. However, this process does not represent genuine new possibilities because the particles that may enter are of the same kind as those already in the system, and, accordingly, the same equations describe them: a generic description is adequate to subsume them. By contrast, biological molecules can do very diverse things, from enzymes to hormones or molecular motors.
Let us take a step back from these somewhat technical aspects. Possibilities in biology are enabled diachronically by constraints, but they are also generated synchronically by them. For example, the bones of an arm generate the possibility of its various positions and enabled the appearance of various claws as well as human tools — the difference between the generation and enablement is the opening of new possibilities in the latter. Moreover, as mentioned above, biological constraints are part of an organization that sustains them and that they contribute to sustaining, for example, by the concept of closure of constraints. Note that this concept does not mean that organizations are static. Instead, enablement can take place at the level of an individual. Moreover, some constraints, called propulsive constraints, contribute to organizations only by enabling the appearance of new constraints ( Miquel & Hwang, 2016 ; Montévil & Mossio, 2020). For example, the mutator mechanism in bacteria leads them to undergo more mutations under stress, thus leading to possible beneficial mutation in response to this stress but without specificity in the mutations triggered. If we shift from the language of constraints to possibilities, this framework implies that possibilities, in biology, are actively sustained by organizations. In the last part of this chapter, we will see that this implies that possibilities may also collapse when organizations are disrupted.
6 How randomness collapses biological diversity
In a nutshell, biological possibilities appear over time and are actively sustained. It is a critical notion that what we call new possibilities are singular or, in a sense, specific, by contrast with generic situations. Biological possibilities are special configurations (among pre-possibilities), and their specificity corresponds to the nature of their contribution to an organization. For example, an enzyme can perform a function because it has a specific sequence.
Now, let us remark that, in the current scientific literature, the term "disruption" is a growing keyword to describe the detrimental impact of human activities on biological organizations. We are in the process of conceptualizing this notion, and we posit that an essential aspect of disruptions in biology is the randomization of the specific configurations that stem from history and are also specific contributions to organizations ( Montévil, 2021 , submitted).
Let us provide two examples. First, let us consider ecosystems where flowering plants and pollinators are mutually dependent. Their interactions require the seasonal synchrony of their feeding and flowering activity, respectively, so that plants undergo sexual reproduction and pollinators do not starve. It follows that ecosystems are in a singular configuration for activity periods. However, different species use different clues to start their activity, and these clues are impacted differently by climate change. It follows that climate change randomizes activity periods, and since the initial, singular situation is the condition of possibility for the different species to maintain each other in the ecosystem, some species are endangered or even disappear ( Burkle et al., 2013 ; Memmott et al., 2007). In this process, part of the possibility space, here the activity periods of the different species, collapses – the dimension of the description space describing the disappearing species disappear.
A second example is the case of endocrine disruptors, which is similar, albeit more complex. Specific amounts of hormones at specific times during development are critical to canalizing developmental processes of cellular differentiation, morphogenesis, and organogenesis leading to viable and fertile adults ( Colborn et al., 1993 ; Demeneix, 2014). Endocrine disruptors randomize hormone action, thus the development process stemming from evolution. These disruptions lead to decreased functions, such as decreased IQ, obesity, loss of fertility, or cancer.
What does this randomization mean? Existing constraints define pre-possibilities, for example, all possible activity periods for the species of an ecosystem; however, only a tiny part of them are genuine possibilities due to the species’ interdependence. Randomization means going from the narrow domain of pre-possibilities that are possibilities (i.e., consistent with their own conditions of possibility) to a larger domain, where part of the possibility space are no longer sustained and thus disappear. This randomization is both an interpretation and a further specification of what Bernard Stiegler called the increase in biological entropy ( Stiegler, 2018). Following Boltzman’s schema, randomization as an increase in entropy means going from a part of a space with specific properties to more generic properties. In biology, though, specific properties result from history and go with viability. Thus this process is primarily a detrimental one.
In a sense, mutations are also this kind of process; most are neutral, others are detrimental, and a few contribute to functions. Mutations illustrate the notion that new possibilities require an exploration of pre-possibilities to find some possibilities among them, thus destabilizing biological organizations. Last, mutations appear at a pace slow enough that they do not destabilize populations, and the impact of detrimental ones is limited by natural selection. If mutations were faster than they are, they would prevent DNA’s role in heredity.
The analysis of disruptions is not specific to anthropogenetic ones; however, the characteristic of the current time is the acceleration and accumulation of disruptions. Many living beings, species, or ecosystems cannot respond to them by generating new possibilities fast enough to compensate for disruptions. In other words, the Anthropocene is, to a large extent, a race between the destructive randomization of existing biological possibilities, and the appearance of new, random possibilities, at all levels of biological organization.
Acknowledgments
This work has received funding from the Cogito Foundation, grant 19-111-R.
References
- Adams, A., Zenil, H., Davies, P., & Walker, S. (2017). Formal definitions of unbounded evolution and innovation reveal universal mechanisms for open-ended evolution in dynamical systems. Scientific Reports, 7(1). https://doi.org/10. 1038/s41598-017-00810-8
- Anderson, C. (2008). The end of theory: The data deluge makes the scientific method obsolete. Wired magazine, 16(7), 16–07. https://www.wired.com/2008/06/pb-theory/
- Biberg, J. (1749). Specimen academicum de oeconomia naturae [tr. fr. in Linné, L’équilibre de la nature, Vrin Paris 1972, p. 57-58.].
- Burkle, L. A., Marlin, J. C., & Knight, T. M. (2013). Plant-pollinator interactions over 120 years: Loss of species, co-occurrence, and function. Science, 339(6127), 1611–1615. https://doi.org/10.1126/science.1232728
- Colborn, T., vom Saal, F. S., & Soto, A. M. (1993). Developmental effects of endocrine-disrupting chemicals in wildlife and humans [PMC1519860[pmcid]]. Environmental health perspectives, 101(5), 378–384. https://doi.org/10.1289/ ehp.93101378
- Darwin, C. (1859). On the origin of species by means of natural selection, or the preservation of favoured races in the struggle for life. John Murray.
- Dawkins, R. (1986). The blind watchmaker: Why the evidence of evolution reveals a universe without design. WW Norton & Company.
- Demeneix, B. (2014). Losing our minds: How environmental pollution impairs human intelligence and mental health. Oxford University Press, USA.
- Gatti, R. C., Fath, B., Hordijk, W., Kauffman, S., & Ulanowicz, R. (2018). Niche emergence as an autocatalytic process in the evolution of ecosystems. Journal of Theoretical Biology, 454, 110–117. https://doi.org/10.1016/j.jtbi.2018.05.038
- Huneman, P. (2007). Understanding purpose: Kant and the philosophy of biology (Vol. 8). University Rochester Press.
- Kant, I. (1790). Critique of judgment [English translation: Pluhar, W. S., 1987. Hackett Publishing. Indianapolis].
- Kapitaniak, M., Strzalko, J., Grabski, J., & Kapitaniak, T. (2012). The three-dimensional dynamics of the die throw. Chaos: An Interdisciplinary Journal of Nonlinear Science, 22(4), 047504. https://doi.org/10.1063/1.4746038
- Kauffman, S. A. (1995). At home in the universe: The search for the laws of self-organization and complexity. Oxford University Press.
- Kauffman, S. A. (2019). A world beyond physics: The emergence and evolution of life. Oxford University Press.
- Lecointre, G. (2018). The boxes and their content: What to do with invariants in biology? In Life sciences, information sciences (pp. 139–152). John Wiley & Sons, Ltd. https://doi.org/10.1002/9781119452713.ch14
- Lecointre, G., & Le Guyader, H. (2006). The tree of life: A phylogenetic classification (Vol. 20). Harvard University Press.
- Longo, G., Miquel, P.-A., Sonnenschein, C., & Soto, A. M. (2012). Is information a proper observable for biological organization? Progress in Biophysics and Molecular biology, 109(3), 108–114. https://doi.org/10.1016/j.pbiomolbio.2012.06.004
- Longo, G., & Montévil, M. (2014). Perspectives on organisms: Biological time, symmetries and singularities. Springer. https://doi.org/10.1007/978-3-642- 35938-5
- Longo, G., & Montévil, M. (2018). Comparing symmetries in models and simulations. In M. Dorato, L. Magnani, & T. Bertolotti (Eds.), Springer handbook of model-based science (pp. 843–856). Springer. https://doi.org/10.1007/978-3- 319-30526-4
- Longo, G., Montévil, M., & Kauffman, S. (2012). No entailing laws, but enablement in the evolution of the biosphere (GECCO’12). Genetic and Evolutionary Computation Conference. https://doi.org/10.1145/2330784.2330946
- Longo, G. (2019). Interfaces of incompleteness. In G. Minati, M. R. Abram, & E. Pessa (Eds.), Systemics of incompleteness and quasi-systems (pp. 3–55). Springer International Publishing. https://doi.org/10.1007/978-3-030-15277-2_1
- Loreto, V., Servedio, V. D. P., Strogatz, S. H., & Tria, F. (2016). Dynamics on expanding spaces: Modeling the emergence of novelties. In M. Degli Esposti, E. G. Altmann, & F. Pachet (Eds.), Creativity and universality in language (pp. 59–83). Springer. https://doi.org/10.1007/978-3-319-24403-7_5
- Memmott, J., Craze, P. G., Waser, N. M., & Price, M. V. (2007). Global warming and the disruption of plant–pollinator interactions. Ecology Letters, 10(8), 710–717. https://doi.org/10.1111/j.1461-0248.2007.01061.x
- Miquel, P.-A., & Hwang, S.-Y. (2016). From physical to biological individuation. Progress in Biophysics and Molecular Biology, 122(1), 51–57. https://doi.org/ 10.1016/j.pbiomolbio.2016.07.002
- Monod, J. (1970). Le hasard et la nécessité. Seuil, Paris.
- Montevil, M. (2021). Computational empiricism : The reigning épistémè of the sciences. Philosophy World Democracy. https://www.philosophy-world-democracy.org/computational-empiricism
- Montévil, M. (2019). Possibility spaces and the notion of novelty: From music to biology. Synthese, 196(11), 4555–4581. https://doi.org/10.1007/s11229-017- 1668-5
- Montévil, M. (2021). Entropies and the anthropocene crisis. AI and society. https://doi.org/10.1007/s00146-021-01221-0
- Montévil, M. (submitted). Disruption of biological processes in the anthropocene: The case of phenological mismatch. https://hal.archives-ouvertes.fr/hal-03574022
- Montévil, M., & Mossio, M. (2015). Biological organisation as closure of constraints. Journal of Theoretical Biology, 372, 179–191. https://doi.org/10. 1016/j.jtbi.2015.02.029
- Montévil, M., & Mossio, M. (2020). The identity of organisms in scientific practice: Integrating historical and relational conceptions. Frontiers in Physiology, 11, 611. https://doi.org/10.3389/fphys.2020.00611
- Montévil, M., Mossio, M., Pocheville, A., & Longo, G. (2016). Theoretical principles for biology: Variation. Progress in Biophysics and Molecular Biology, 122(1), 36–50. https://doi.org/10.1016/j.pbiomolbio.2016.08.005
- Paley, W. (1802). Natural theology: Or, evidences of the existence and attributes of the deity. J. Faulder.
- Soros, L., & Stanley, K. O. (2014). Identifying necessary conditions for open-ended evolution through the artificial life world of chromaria. ALIFE 14: The Fourteenth Conference on the Synthesis and Simulation of Living Systems, 14, 793–800. https: //doi.org/10.7551/978-0-262-32621-6-ch128
- Stiegler, B. (2018). The neganthropocene. Open Humanites Press.
- Tenaillon, O., Taddei, F., Radman, M., & Matic, I. (2001). Second-order selection in bacterial evolution: Selection acting on mutation and recombination rates in the course of adaptation. Research in Microbiology, 152(1), 11–16. https://doi.org/ 10.1016/S0923-2508(00)01163-3
- Walsh, D. M. (2020). Action, program, metaphor. Interdisciplinary Science Reviews, 45(3), 344–359. https://doi.org/10.1080/03080188.2020.1795803