Here we discuss the application and articulation of biological principles for mathematical modeling of morphogenesis in the case of mammary ductal morphogenesis, with an emphasis on the default state.
Abstract
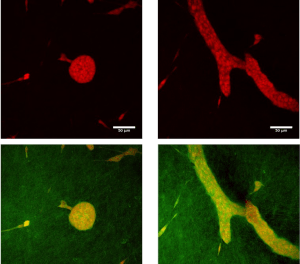
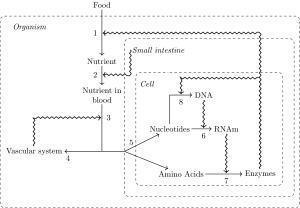
Unlike inert objects, organisms and their cells have the ability to initiate activity by themselves, and thus change their properties or states even in the absence of an external cause. This crucial difference led us to search for principles suitable for the study organisms. We propose that cells follow the default state of proliferation with variation and motility, a principle of biological inertia. This means that in the presence of sufficient nutrients, cells will express their default state. We also propose a principle of variation that addresses two central features of organisms, variation and historicity. To address interdependence between parts, we use a third principle, the principle of organization: more specifically, the notion of the closure of constraints. Within this theoretical framework, constraints are specific theoretical entities defined by their relative stability with respect to the processes they constrain. Constraints are mutually dependent in an organized system and act on the default state. <br>Here we discuss the application and articulation of these principles for mathematical modeling of morphogenesis in a specific case, that of mammary ductal morphogenesis, with an emphasis on the default state. Our model has both a biological component, the cells, and a physical component, the matrix that contains collagen fibers. Cells are agents that move and proliferate unless constrained; they exert mechanical forces that i) act on collagen fibers and ii) on other cells. As fibers are organized, they constrain the cells’ ability to move and to proliferate. This model exhibits a circularity that can be interpreted in terms of the closure of constraints. Implementing our mathematical model shows that constraints to the default state are sufficient to explain the formation of mammary epithelial structures. Finally, the success of this modeling effort suggests a step-wise approach whereby additional constraints imposed by the tissue and the organism can be examined in silico and rigorously tested by in vitro and in vivo experiments, in accordance with the organicist perspective we embrace.
The collective work that produced this book is based on the claim that today's destructive development model is reaching its ultimate limits, and that its toxicity is generated above all by the fact that the current industrial economy is based on an obsolete physical model.
Abstract
Bifurcating means: reconstituting a political economy that reconnects local knowledge and practices with macroeconomic circulation and rethinks territoriality at its different scales of locality; developing an economy of contribution on the basis of a contributory income no longer tied to employment and once again valuing work as a knowledge activity; overhauling law, and government and corporate accounting, via economic and social experiments, including in laboratory territories, and in relation to cooperative, local market economies formed into networks and linked to international trade; revaluing research from a long-term perspective, independent of the short-term interests of political and economic powers; reorienting digital technology in the service of territories and territorial cooperation. <br> The collective work that produced this book is based on the claim that today’s destructive development model is reaching its ultimate limits, and that its toxicity, which is increasingly massive, manifest and multidimensional (medical, environmental, mental, epistemological, economic – accumulating pockets of insolvency, which become veritable oceans), is generated above all by the fact that the current industrial economy is based in every sector on an obsolete physical model – a mechanism that ignores the constraints of locality in biology and the entropic tendency in reticulated computational information. In these gravely perilous times, we must bifurcate: there is no alternative.
Comment concevoir et réaliser des plateformes numériques au service des relations sociales et intergénérationnelles, aujourd’hui menacées par les applications addictives et l’économie des données ?
Abstract
Lorsque les technologies numériques sont mises au service de l’économie des données, leur design et leur fonctionnement exploitent les attentions, afin d’orienter, voire de contrôler, les comportements des utilisateurs. Réduits à un ensemble de processus cognitifs et de réactions réflexes, ils se voient dépossédés de leurs savoirs, alors même que, dans nos sociétés en situation de crise sanitaire, sociale, politique et écologique, le partage et la transmission des savoir-faire, des savoir-vivre et des savoir-penser sont plus que jamais nécessaires. <br> Comment concevoir et réaliser des plateformes numériques au service des relations sociales et intergénérationnelles, aujourd’hui menacées par les applications addictives et l’économie des données ? Comment intégrer dans les dispositifs computationnels des fonctions délibératives et interprétatives ? Comment transformer les technologies numériques en supports de mémoire et de savoirs ? Comment mettre les algorithmes au service de l’intelligence collective ? En un mot, comment prendre soin de l’informatique pour les générations actuelles et à venir ? Ce livre interroge la manière dont les supports techniques configurent nos capacités psychiques et nos relations collectives, et propose des solutions pour concevoir de nouveaux dispositifs et de nouvelles pratiques, afin de mettre les technologies numériques au service de la production et de la transmission de savoirs, ainsi que des liens entre les générations.
Pour progresser sur la question du rapport entre l’informatique et le calculable, je propose de réinterpréter l’objet de l’informatique théorique.
Abstract
Pour progresser sur la question du rapport entre l’informatique et le calculable, je propose de réinterpréter l’objet de l’informatique théorique puis de faire un détour par la biologie théorique où la question d’un symbole qui empêche de calculer se pose. Enfin, je reviens vers l’informatique en transférant de manière critique certains concepts issus de mes travaux en biologie théorique.
Qu'est qu'une forme en biologie? Au delà des définitions mathématiques, quel est le statut théorique des formes biologiques?
Abstract
Dans l’interface entre biologie et mathématiques, les formes et les processus de morphogenèse sont souvent étudiées pour eux-mêmes. Nous pensons que cette manière de procéder est insuffisante pour capturer le sens biologique de ces formes. La biologie comporte des spécificités qui se manifestent tant sur le plan philosophique que sur celui des principes théoriques : en particulier, tout processus biologique tel qu’un processus de morphogenèse ou une régulation physiologique (i) s’inscrit dans l’évolution et dans une histoire naturelle et (ii) s’intègre dans un organisme dont il dépend et auquel il participe. Nous aborderons alors le sens des formes biologiques à l’aune de ces principes, tant au niveau de la théorie qu’au niveau de la compréhension de l’accès expérimental aux objets biologiques.
Most mathematical modeling in biology rely on the epistemology of physics. By contrast, we argue that historicity comes first in biology.
Abstract
Most mathematical modeling in biology relies either implicitly or explicitly on the epistemology of physics. The underlying conception is that the historicity of biological objects would not matter to understand a situation here and now, or, at least, historicity would not impact the method of modeling. We analyze that it is not the case with concrete examples. Historicity forces a conceptual reconfiguration where equations no longer play a central role. We argue that all observations depend on objects defined by their historical origin instead of their relations as in physics. Therefore, we propose that biological variations and historicity come first, and regularities are constraints with limited validity in biology. Their proper theoretical and empirical use requires specific rationales.
We propose a theoretical framework to model the behavior of cells in tissues and develop an application in the case of duct morphogenesis in mammary glands.
Abstract
We developed 3D culture methods that reproduce in vitro mammary gland ductal morphogenesis. We are proposing a conceptual framework to understand morphogenetic events based on epistemologically sound biological principles instead of the common practice of using only physical principles. More specifically, our theoretical framework is based on the principle that the default state of cells is proliferation with variation and motility. We emphasize the role played by the agency of cells embedded in a gel and the circularity that is relevant for the intended process, whereby cells act upon other cells and on matrix elements, and are subject to the agentivity of neighboring cells. This circularity strongly differs from classical linear causality. Finally, our approach opens up the study of causal determination to multilevel explanations rather than to reductive ones involving only molecules in general and genes in particular.
Keywords: Morphogenesis, extracellular matrix, theoretical principles, default state of cells, modelization.
We developed a mathematical model of mammary gland based on proper biological principles: the default state of cells and the principle of organization.
Abstract
Abstract In multicellular organisms, relations among parts and between parts and the whole are contextual and interdependent. These organisms and their cells are ontogenetically linked: an organism starts as a cell that divides producing non-identical cells, which organize in tri-dimensional patterns. These association patterns and cells types change as tissues and organs are formed. This contextuality and circularity makes it difficult to establish detailed cause and effect relationships. Here we propose an approach to overcome these intrinsic difficulties by combining the use of two models; 1) an experimental one that employs 3D culture technology to obtain the structures of the mammary gland, namely, ducts and acini, and 2) a mathematical model based on biological principles. The typical approach for mathematical modeling in biology is to apply mathematical tools and concepts developed originally in physics or computer sciences. Instead, we propose to construct a mathematical model based on proper biological principles. Specifically, we use principles identified as fundamental for the elaboration of a theory of organisms, namely i) the default state of cell proliferation with variation and motility and ii) the principle of organization by closure of constraints. This model has a biological component, the cells, and a physical component, a matrix which contains collagen fibers. Cells display agency and move and proliferate unless constrained; they exert mechanical forces that i) act on collagen fibers and ii) on other cells. As fibers organize, they constrain the cells on their ability to move and to proliferate. The model exhibits a circularity that can be interpreted in terms of closure of constraints. Implementing the mathematical model shows that constraints to the default state are sufficient to explain ductal and acinar formation, and points to a target of future research, namely, to inhibitors of cell proliferation and motility generated by the epithelial cells. The success of this model suggests a step-wise approach whereby additional constraints imposed by the tissue and the organism could be examined in silico and rigorously tested by in vitro and in vivo experiments, in accordance with the organicist perspective we embrace.
In the search of a theory of biological organisms, we propose to adopt organization as a theoretical principle and define it as closure of constraints.
Abstract
Abstract In the search of a theory of biological organisms, we propose to adopt organization as a theoretical principle. Organization constitutes an overarching hypothesis that frames the intelligibility of biological objects, by characterizing their relevant aspects. After a succinct historical survey on the understanding of organization in the organicist tradition, we offer a specific characterization in terms of closure of constraints. We then discuss some implications of the adoption of organization as a principle and, in particular, we focus on how it fosters an original approach to biological stability, as well as and its interplay with variation.
We articulate three principles for a theory of organisms proposed, namely: the default state the principle of variation and the principle of organization.
Abstract
Abstract Organisms, be they uni- or multi-cellular, are agents capable of creating their own norms; they are continuously harmonizing their ability to create novelty and stability, that is, they combine plasticity with robustness. Here we articulate the three principles for a theory of organisms, namely: the default state of proliferation with variation and motility, the principle of variation and the principle of organization. These principles profoundly change both biological observables and their determination with respect to the theoretical framework of physical theories. This radical change opens up the possibility of anchoring mathematical modeling in biologically proper principles.
We propose a biological default state of proliferation with variation and motility by analogy with physics inertia. Then, quiescence requires an explanation.
Abstract
Abstract The principle of inertia is central to the modern scientific revolution. By postulating this principle Galileo at once identified a pertinent physical observable (momentum) and a conservation law (momentum conservation). He then could scientifically analyze what modifies inertial movement: gravitation and friction. Inertia, the default state in mechanics, represented a major theoretical commitment: there is no need to explain uniform rectilinear motion, rather, there is a need to explain departures from it. By analogy, we propose a biological default state of proliferation with variation and motility. From this theoretical commitment, what requires explanation is proliferative quiescence, lack of variation, lack of movement. That proliferation is the default state is axiomatic for biologists studying unicellular organisms. Moreover, it is implied in Darwin’s “descent with modification”. Although a “default state” is a theoretical construct and a limit case that does not need to be instantiated, conditions that closely resemble unrestrained cell proliferation are readily obtained experimentally. We will illustrate theoretical and experimental consequences of applying and of ignoring this principle.
We characterize biological organization as a closure of constraints, where constraints are defined at a given time scale and are interdependent.
Abstract
We propose a conceptual and formal characterisation of biological organisation as a closure of constraints. We first establish a distinction between two causal regimes at work in biological systems: processes, which refer to the whole set of changes occurring in non-equilibrium open thermodynamic conditions; and constraints, those entities which, while acting upon the processes, exhibit some form of conservation (symmetry) at the relevant time scales. We then argue that, in biological systems, constraints realise closure, i.e. mutual dependence such that they both depend on and contribute to maintaining each other. With this characterisation in hand, we discuss how organisational closure can provide an operational tool for marking the boundaries between interacting biological systems. We conclude by focusing on the original conception of the relationship between stability and variation which emerges from this framework.
Keywords: Biological organisation, Closure, Constraints, Symmetries, Time scales
