We suggest a simple functional representation of biological protention and introduce abstract notions of biological inertia and extended present.
Abstract
This article proposes an abstract mathematical frame for describing some features of cognitive and biological time. We focus here on the so called extended present as a result of protentional and retentional activities (memory and anticipation). Memory, as retention, is treated in some physical theories (relaxation phenomena, which will inspire our approach), while protention (or anticipation) seems outside the scope of physics. We then suggest a simple functional representation of biological protention. This allows us to introduce the abstract notion of biological inertia.
Keywords: Memory and Cognition, protention, retention, biological time
In this paper, we provide a general characterization of closure as a distinctive causal regime of autonomous systems, which cannot be reduced to physico-chemical causation without loosing relevant information about the system’s organization. Our argument consists in three steps. First, we put forward an account of how different levels of causation can be realized within a biological autonomous systems, by making a conceptual and formal distinction, based on the idea of symmetry, between processes and constraints exerted on these processes. Second, we develop the notion of dependence among constraints and, third, we claim that closure is realized as a mutual dependence among a set of entities having the status of constraints within the system. The paper might then make a relevant contribution to the elaboration of a conceptual and formal theory of closure, able to overcome some of the weaknesses of previous accounts.
Symmetries play a critical role in physics. By contrast, symmetry changes are ubiquitous for biological organisms, leading to deep theoretical consequences.
Abstract
Symmetries play a major role in physics, in particular since the work by E. Noether and H. Weyl in the first half of last century. Herein, we briefly review their role by recalling how symmetry changes allow to conceptually move from classical to relativistic and quantum physics. We then introduce our ongoing theoretical analysis in biology and show that symmetries play a radically different role in this discipline, when compared to those in current physics. By this comparison, we stress that symmetries must be understood in relation to conservation and stability properties, as represented in the theories. We posit that the dynamics of biological organisms, in their various levels of organization, are not just processes, but permanent (extended, in our terminology) critical transitions and, thus, symmetry changes. Within the limits of a relative structural stability (or interval of viability), variability is at the core of these transitions.
Keywords: Symmetries, Systems biology, Critical transitions, Levels of organization, Hidden variables, Coherent structures, downward causation
We frame several features of biological time with a 2-d manifold to accommodate autonomous biological rhythms both for individuals and comparisons.
Abstract
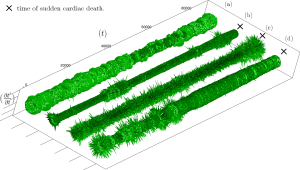
This paper proposes an abstract mathematical frame for describing some features of biological time. The key point is that usual physical (linear) representation of time is insufficient, in our view, for the understanding key phenomena of life, such as rhythms, both physical (circadian, seasonal …) and properly biological (heart beating, respiration, metabolic …). In particular, the role of biological rhythms do not seem to have any counterpart in mathematical formalization of physical clocks, which are based on frequencies along the usual (possibly thermodynamical, thus oriented) time. We then suggest a functional representation of biological time by a 2-dimensional manifold as a mathematical frame for accommodating autonomous biological rhythms. The “visual” representation of rhythms so obtained, in particular heart beatings, will provide, by a few examples, hints towards possible applications of our approach to the understanding of interspecific differences or intraspecific pathologies. The 3- dimensional embedding space, needed for purely mathematical reasons, allows to introduce a suitable extra-dimension for “representation time”, with a cognitive significance.
