The Hitchhiker’s Guide to the Cancer Galaxy: How two critics missed their destination
Organisms. Journal of Biological Sciences
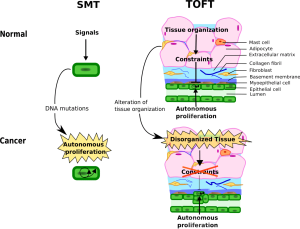
Two theories aim to understand cancer: the reductionist Somatic Mutation Theory (SMT) and the organicist Tissue Organization Field Theory (TOFT).
Abstract
Two main theories aim at understanding carcinogenesis: the reductionist smt locates cancer in cancer cells, while the organicist toft locates cancer at the tissue level. For toft, the ‘cancer cell’ is a phlogiston, smt is an old paradigm which ought to be replaced. Recently two critics have argued that toft and smt, despite their apparent strong incompatibilities, are actually compatible. Here we review their arguments. We show that these arguments are based on interpretation mistakes that become understandable once one grants that criticizing a paradigm from the point of view of another, in which words do not have the same signification, bears the risk of strong misunderstandings. These misunderstandings, in our experience, are common. We hope that this discussion will help clarifying the differences between toft and smt.
Keywords: TOFT, reductionism, organicism, levels of organization, SMT