In search of principles for a Theory of Organisms
Journal of biosciences
Lacking an operational theory to understand life cycles hinders progress in biology. We discuss elements towards such a theory, such as inertia and thermodynamics.
Abstract
Lacking an operational theory to explain the organization and behaviour of matter in unicellular and multicellular organisms hinders progress in biology. Such a theory should address life cycles from ontogenesis to death. This theory would complement the theory of evolution that addresses phylogenesis, and would posit theoretical extensions to accepted physical principles and default states in order to grasp the living state of matter and define proper biological observables. Thus, we favour adopting the default state implicit in Darwin’s theory, namely, cell proliferation with variation plus motility, and a framing principle, namely, life phenomena manifest themselves as non-identical iterations of morphogenetic processes. From this perspective, organisms become a consequence of the inherent variability generated by proliferation, motility and self-organization. Morphogenesis would then be the result of the default state plus physical constraints, like gravity, and those present in living organisms, like muscular tension.
Keywords: Animals, Biological Evolution, Biophysics/methods, Cell Division, Mice, Models, Morphogenesis, Thermodynamics
Table of contents
Reading time: ~51 min
In Search of Principles for a Theory of Organisms
Abstract
Lacking an operational theory to explain the organization and behavior of matter in unicellular and multicellular organisms hinders progress in biology. Such a theory should address life cycles from ontogenesis to death. This theory would complement the theory of evolution that addresses phylogenesis, and would posit theoretical extensions to accepted physical principles and default states in order to grasp the living state of matter and define proper biological observables. Thus, we favor adopting the default state implicit in Darwin’s theory, namely, cell proliferation with variation plus motility, and a framing principle, namely, life phenomena manifest themselves as non-identical iterations of morphogenetic processes. From this perspective organisms become a consequence of the inherent variability generated by proliferation, motility and self-organization. Morphogenesis would then be the result of the default state plus physical constraints, like gravity, and those present in living organisms, like muscular tension.
Keywords: Biological organization, autopoiesis, default state, emergence, development, mathematical symmetries, criticality
(Einstein, oral remark quoted in Salam 1990)
1.Motivation
Biologists acknowledge a crisis in their midst: on the one hand, reams of data acquired from a reductionist perspective (for example, “transcriptomics”) do not provide the anticipated understanding of the subject matter of their interest. On the other hand, the application of mathematical modeling has not helped much either. This is due in part to the preponderance of “pragmatic systems biology,” a practice that emphasizes large-scale molecular interactions which is technology-driven and does not claim explicit theory commitments (O'Malley and Dupre 2005).
2.The role of theories
At the beginning of the Scientific Revolution, scientists thought that they had direct access to their outside world: God’s will was to make nature intelligible to creatures like us. The separation of science and religion was a long and complex process: Kant's philosophy and Darwin’s theory were major contributors to this separation. Ever since, scientists acknowledge that they are inside the world they wish to observe and study. As a result of this realization, objectivity had to be constructed through scientific theories that would provide intelligibility principles to frame observations, experiments and explanations. In the 16th and 17th centuries, physicists developed theories that provided an accurate description of phenomena of the inert. In this theory-rich context, scientists were aware that theories determine which are the proper observables while, conversely, the choice of observables was a major theoretical commitment. For example, the decision to investigate the relationship between pressure, volume and temperature well before considering the atomic structure of gases (XVII century, Boyle and Mariotte), allowed to develop a theory at that level of observability. Further work at the macroscopic level originated modern thermodynamics (TD) as yet another major achievement of the XIX century; this was well before Boltzmann's unification with an atomistic perspective. Notwithstanding, atoms and molecules are proper observables in another physical theory, Quantum Mechanics (QM).
When living entities die, they decompose into particles of inert matter, and in turn, living organisms assemble the same inert matter in novel ways. The emergence of these novelties requires suitable theoretical constructs (;Sa çlioglu et al. 2014)( Longo G and Montevil M 2014 Perspectives on Organisms: Biological Time, Symmetries and Singularities (Berlin: Springer).) That is, besides the already acknowledged physical principles and default states, additional principles and theoretical requirements are needed to describe proper biological observables, such as phenotypes. These extensions of physical laws into biology must be compatible with physical theory about inert matter, i.e., organisms should not violate the laws of thermodynamics, gravity or the quantum properties of their component particles. Yet, these principles may not suffice to make the biological dynamics intelligible at the phenotypic level.
In biology, other than Darwin’s theory of evolution (1859), the creation of global theories has not been as successful as in physics (Soto and Sonnenschein 2012). Among other subjects, Darwin’s theory on the origin of species addressed common descent, encompassed a long time-frame and provided an adequate explanation of phylogeny. The fundamental principles in Darwin’s theory are a) descent with modification and b) natural selection. However, biology has yet to produce a theory of organisms that would encompass ontogeny and life cycles, i.e., phenomena occurring on a time-scale going from conception to death (Elsasser 1987).
Recently, several worthy contributions have been made in this area (Davies, Deacon, Newman Kupiec). Approaches based exclusively on stochasticity and natural selection like the ontophylogenesis theory (Kupiec 2010) provide new perspectives; however, they are insufficient to frame a theory of organisms because the molecular events at the core of the ontophylogenesis theory are causally dependent on cell, tissue and organismal contexts and these contexts are not addressed by this approach.
Since the 1970’s, the thermodynamics of dissipative systems provided an opportunity to examine the relevance of self-organizing physical systems to the understanding of the emergence of life, as exemplified by the pioneering work of Prigogine and his school (Nicolis and Prigogine 1977), Kauffman (Kauffman 1993) and others. For instance, Cottrell elegantly highlighted the role of thermodynamics while stressing the need for a biological perspective that would bring to this analysis distinctive biological characteristics such as historicity and purposiveness (Cottrell 1979). Unfortunately, despite these promising beginnings, the development of a theory of organisms has been hindered by the misuse of metaphors borrowed from theories of information (Longo et al. 2012a). To remedy this situation, we are proposing instead explicit principles for the elaboration of a theory of organisms that would make such a theory robust, and open to change when challenged by empirical evidence.
Our analysis purposefully refers to physics, not only because biological theory should not violate physical laws, but also because there is a tradition in organismal biology to use both the similarities and differences between these disciplines to advance biological knowledge. For example, Helmholtz improved the understanding of both the physiology of nerve conduction and muscle metabolism while developing the principle of conservation of energy in physics (Lenoir 1982). An additional example is the current wave of physicists and mathematicians entering the field of Systems Biology while carrying with them the theoretical framework of physics[3]. Most importantly, biology may make it possible to identify a new physical principle (Moore 2012). Therefore, before stating the proposed principles for a theory of organisms, we will elaborate on some relevant relationships between physics and biology (Table 1).

3.From physics to biology
3.1 The impact of Physics on Biology
First, we will go over the fundamental role that symmetries and conservation principles play in physical theories, in particular by defining the default state. Then, we will discuss the appearance of new observables, which is related to the concept of emergence, and how these concepts relate to symmetries and conservation principles. We will then posit that biology is characterized by a relentless breaking of symmetries, and propose a theoretical bridge between physics and biology which we are calling extended criticality. Extended criticality provides the theoretical frame for a non-conservative default state. The latter entails an intrinsic source of variation, which is a necessary concept in evolutionary biology together with a principle of non-identical iteration of morphogenetic processes.
3.2 Default states and symmetries in physics
3.3 Emergence in physics and in biology
3.4 From criticality to extended criticality
From the view point of extended critical transitions an organism is understood as being in a permanent transition with all the main signatures of criticality, such as changes of symmetries, the constant reconstruction of correlation lengths and the formation of a new global structure (Bailly and Longo 2011;Longo and Montevil 2014) (Table 1). Thus, phylogenetic and ontogenetic trajectories involve “cascades of symmetry changes” which contribute to the historicity of phylogeny and ontogeny by generating biological variability and anatomical and functional diversity (Longo et al. 2012b;Longo and Montevil 2014). This is the first of the points we wish to make regarding the unity of these two theories addressing life at different time-scales.

3.5 Physical systems at equilibrium, far-from-equilibrium and organisms
In an organism, each cell division changes local symmetries because each of those divisions forces new local and potentially global correlations. These changes yield variability and adaptability to organisms. In the context of evolution, the advent of new functions and organs are additional examples of symmetry changes. In our approach, reproduction with modification involves “symmetry changes” and may be viewed as multiple critical transition s which span the irreversible time of both ph ylogenesis and ontogenesis. This is the third common point towards the unification of the theories addressing these two different time-scales.
4.Foundations for a theory of organisms
We propose two founding principles: 1) the default state of cells, meaning proliferation with variation and motility, and 2) the framing principle of non-identical iterations of a morphogenetic process. These principles take place in the context of extended critical transitions.
4.1 The default state in Biology: a nexus between the theories of evolution and of organisms
In order to provide a theoretical transition between physics and biology, we will define a default state which is a limit case. Inertial movement as uniform rectilinear movement is a limit state and physicists made all physical movements intelligible as departures from it. By describing this default state, Galileo could focus on the analysis of the forces constraining it, such as gravity and friction.
4.1.1 - Proliferation with variation
Darwin explicitly stated “… There is no exception to the rule that every organic being naturally increases at so high a rate, that, if not destroyed, the earth would soon be covered by the progeny of a single pair” (Darwin 1909). Reproduction obligatorily involves “modification” (descent with modification, in Darwin’s words). Reproduction with variation is intrinsic to organisms regardless of whether they are unicellular or multicellular (Sonnenschein and Soto 1999;Soto and Sonnenschein 2011). Darwin's narrative implies that reproduction with variation is a default state and he describes it as a limit case. This is the third, and probably most important, point in common between the theories of evolution and organisms.
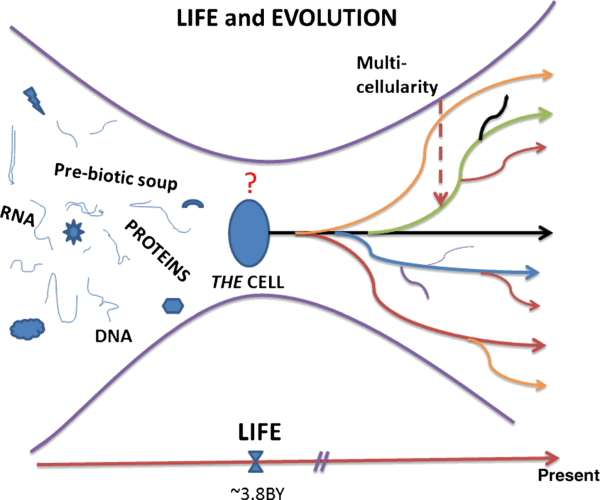
The default state of proliferation applies to the first common ancestor, i.e., the cell from which all organisms arose (Figure 2). In fact, microbiologists consider axiomatic that proliferation is the default state of prokaryotes and unicellular eukaryotes (Luria 1975). On the contrary, despite lacking evidence, there had been a consensus among biologists that consider quiescence as the default state of cells in multicellular organisms (Alberts et al. 2008;Alberts 2010). We posited, instead, that proliferation was retained as the default state with the advent of metaphyta and metazoa. This conclusion is supported by the conservation of the cell cycle components throughout eukaryotes (Sonnenschein and Soto 1999) and by experimental evidence (Leitch et al. 2010;Sonnenschein et al. 1996;Sonnenschein and Soto 1999;Soto and Sonnenschein 1985;Ying et al. 2008). Additionally, the default state of proliferation has been adopted advantageously as a fundamental principle in theories of carcinogenesis and of development (Minelli 2011;Sonnenschein and Soto 1999;Soto and Sonnenschein 2010).
Variation (as in proliferation with variation) should be understood as symmetry changes; each cell division generates variations that correspond to symmetry changes associated to critical transitions. How does intrinsic variation manifest itself? One obvious example is the unequal distribution of macromolecules and organelles during cell division (Huh and Paulsson 2011); another is stochastic gene expression (Kupiec 1983;Marinov et al. 2014;Ta niguchi et al. 2010;Tyagi 2010). Additional variation is due to somatic mutations and aneuploidy, events described among cells of normal mammalian kidneys and brains (Martin et al. 199 6;Rehen et al. 2001).
4.1.2 – Motility
Motility should not exclude movements other than locomotion. Plants may be attached to the ground by their roots, but they can generate movement of their parts, for example by growing towards a source of light. Flowers and leaves open and close in response to light (van Doorn and van Meeteren 2003), and like animal cells, can move organelles using actin and myosin (Ueda et al. 2010).
4.2 Default state and constraints
During early development, increases in the size of an organism occur by generation of new cells and production of extracellular matrix. Cell proliferation is the result of the default state and is constrained. Organ shape is a result of the cells’ default state plus physical constraints, like gravity, and those ones created by the living organism, like muscular tension.
Inert matter requires causes to change states or properties. The causal structure of a physical process is determined mathematically by a set of equations justified by symmetries, such as equilibria. For example, Newton’s equations relate forces to their effects, i.e., as causes of acceleration at equilibrium. In physics, causes and constraints on the default state are synonymous. Organisms, instead, are agentive and thus capable of initiating activity by themselves. The default state is a cause in biology; by contrast, anything that affects the default state is a constraint. For example, gravity becomes a constraint for evolution and embryogenesis, and not a cause of biological dynamics. Gravity influences numerous if not all biological processes and it is a main determinant of morphogenesis as exemplified in the formation of the anteroposterior axis in chick embryos. However, the formation of this axis is not a consequence of gravitation, but of the activity of cells under the constraint of gravitation: in our theoretical frame and language, gravity is a constraint and not a cause. In sum, biological dynamics is grounded in the default state, that is, proliferation with variation and motility
Constraints narrow down the range of “possibles”. For example, fibroblasts removed from subcutaneous tissues of an animal have the same size when dissociated and explanted into a culture dish. Soon after, their size varies over a wide range (Rubin 1988;Rubin and Hatie 1968). Constraints also enable other “possibles.” The bottom of a cell culture dish prevents displacement in that direction reducing the possible movements, but at the same time this constraint enables cells to crawl along a plastic surface. In a multicellular organism, other constraints to the default state are relevant. Mechanical constraints limit proliferation, variation and motility, like when cells compress each other; they adhere to other cells, and stretch each other. Fibers in the extracellular matrix apply tensile forces on structures allowing movement in certain directions and constraining it in others (Barnes et al. 2014). Sequential smooth muscle differentiation exerts compressive stress on the endoderm and mesenchyme of the small intestine, causing buckling and folding which leads to the formation of villi (Shyer et al. 2013). Muscle contraction shapes the bones to which they are attached by inducing tissue accrual on the side of tension (Muller 2003;Rot-Nikcevic et al. 2007), and chemical interactions may also constrain the default state, as when serum albumin restricts proliferation of estrogen sensitive cells, and estrogen cancels the action of this constraint (Sonnenschein et al. 1996).
We posit that organisms do not have stable symmetries that would allow us to spell out the actual phylogenetic and ontogenetic trajectories that they follow because such trajectories depend on the history and random changes of symmetries of the objects considered, organisms in this case (Longo and Montevil 2014).. The default state of proliferation with variation corresponds to Darwin's key idea of evolution being “descent with modification”, on which selection operates.
In contrast to physics where conservation principles frame the theories, in biology, the default state of proliferation with variation is a non-conservation principle (Longo et al. 2012b;Longo and Montevil 2013). This rationale does not conflict with physical principles as it concerns new observables, i.e., phenotypes. In fact, proper principles and observables are being added at different and interacting levels of biological organization and determination. Thus, the theory of organisms that we envisage becomes a compatible extension of physical theories.
Finally, the recent phylogenetic history of every cell is the proliferation of its parental cell. On a far longer temporal scale unicellular ancestors of cells of multicellular organisms are assumed to have had proliferation as their default state. Thus, it is the shift from proliferation with variation and motility to quiescence, which should be explained, instead of being assumed. Cell proliferation is achieved by the execution of a cell cycle process, which does not stop until two quite similar but non-identical cells are formed. The cell cycle is a representation of enzymatic reactions and physical processes leading to the duplication of the cell components including DNA, and the faithful separation of two daughter cells. Textbooks use the metaphor of the cycle operating like a dishwasher performing a series of stereotyped tasks (Alberts et al. 1994). If quiescence were its default state, it would be difficult to activate the “cell cycle machine” by organizing the cell cycle components which entail a very complex network of constraints. Instead, when proliferation is the default state, it becomes easier to prevent complex machinery from functioning: a simple mechanical or chemical constraint may suffice. For example, a switch will do it for an engine and an inhibitor will do it for a cell. To sum the situation up, the difference between proliferation or quiescence as a default state corresponds to the difference between preventing something complex from happening and causing it to happen. The latter is much harder to conceive, explain and realize.
4.3 The framing principle of biological morphogenesis
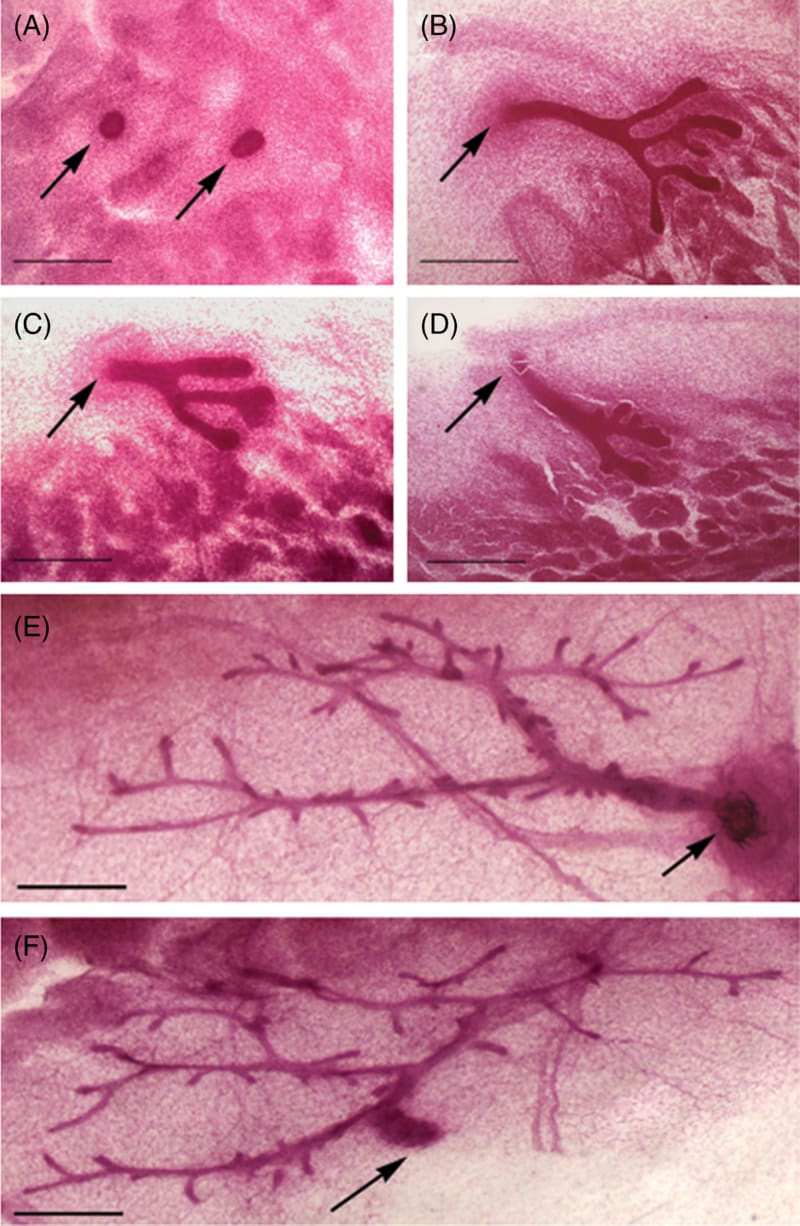
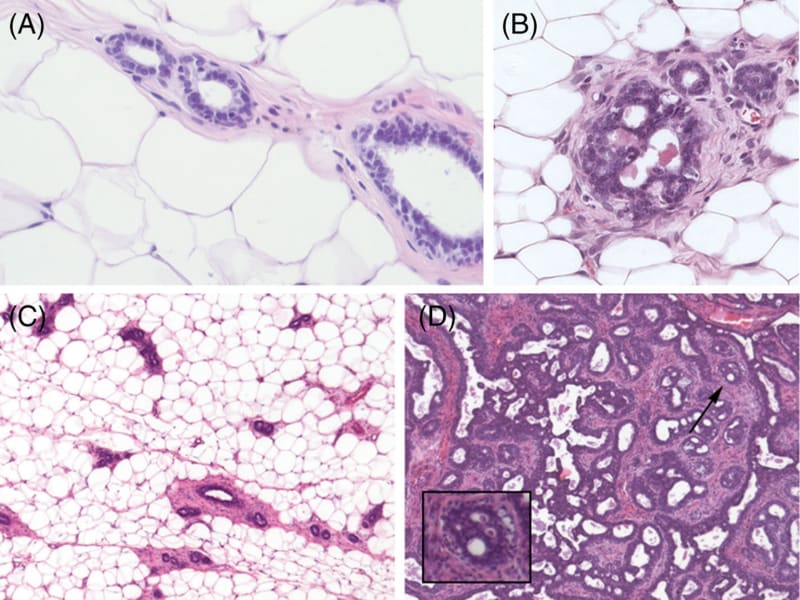
Generating phenotypes from a single cell, be it LUCA (Last Common Universal Ancestor) (Steele and Penny 2010) or a zygote, is an essential component of phylogenesis and ontogenesis. Organisms, be they unicellular or multicellular, are a consequence of the inherent variability generated by proliferation, motility and self-organization (Mossio and Moreno 2010), all of which operate within the framing principle we propose: life phenomena are non-identical iterations of a morphogenetic process by which organization is iterated and maintained (Table 1). For example, branching morphogenesis is a ubiquitous process that generates a repetitive, yet non-identical pattern whereby length of branches and branching angles vary (Figure 3).
4.4 Complexity versus organization
5.Implications for biological research
What are the benefits of adopting the principles for a theory of organisms delineated above? First, the proposed principles would help to move away from operational definitions. From the notion of gene to that of growth factor, the use of operational definitions has resulted in contradictions and ambiguities that hinder the establishment of general and stable concepts (Moss 2003;Sonnenschein and Soto 1999). Additionally, the proposed principles enable alternative explanations to the mechanistic ones inherent to the molecular biology revolution. The latter do not represent an explicit theoretical frame, but mostly refer metaphorically to common sense notions, such as “information” and “program”., The use of these metaphors forces explanations to be molecular and to follow predictable causal chains (Longo et al. 2012a). Instead, by insisting on the search of constraints to the default state, multilevel biomechanical and bioelectrical explanations become as legitimate as molecular ones.
Second, our principles radically change both observables and determination vis a vis the theoretical frames proposed by physical theories. Such a change enables us to anchor reasoning and modelization on robust biological principles. Indeed, as implied by Turing, there is an epistemological gap between modelization and imitation (Turing 1950;Turing 1952). While the former is based on a theory concerning the object of knowledge, the latter is not. For example, individuation becomes the result of non-identical morphogenetic iterations. This principle excludes a Platonic conception of ideal- or perfect organs or structures which would be determined as an optimal solution of an equation.
Third, the principles we propose enable the construction and discussion of mathematical models on the bases of biologically relevant assumptions. For example, in ecology the commonly used equations addressing population size are not theory-based. Taking into consideration the default state and the notion of constraint it is feasible to obtain theoretically meaningful equations in which the food term is not a cause per se: this constraint becomes relevant only when there is scarcity of food. In an ecological context there are numerous parameters that enable the population to grow in number, however, those parameters actually play a role on growth (i.e., the growth rate) only when they are limiting the increase of the population. Food superabundance will not make the population grow faster.
Fourth, we are proposing an alternative to the use of the notions of program, information, and signal specificity in biology. In particular, biological variation is not noise as in those information-based theories (Huang 2009). Rather than as a priori determination as presupposed by the notion of developmental program, the two proposed principles lead to a conception of biological specificity that is defined directly with respect to the trajectory of organisms and their cells in time and space as a cascade of symmetry changes.
6.Conclusions
Research on organismal biology is being conducted in the absence of a global theory. Instead, its conceptual framework is loosely based on the mathematical theories of information and on operational definitions. This combination of notions has generated contradictions and hindered progress. In spite of a few successful outcomes, the application of physical principles without proper analysis of the differences between biological and physical situations has also contributed to the current crisis. O ur analysis of the differences between the physics of inanimate and living matter provides a sound perspective for the construction of a much needed theory of organisms while providing founding principles adequate for framing experiments and mathematical modeling.
Acknowledgements:
This work was conducted as part of the research project “Addressing biological organization in the post-genomic era” which is supported by the International Blaise Pascal Chairs, Region Ile de France. AMS is the incumbent Blaise Pascal Chair of Biology at the École Normale Supérieure and GL is the Chair’s host. Additional support was provided by grants from the Avon Foundation, the Italian Space Agency and the National Institute of Environmental Health Sciences of the NIH (ES08314 and U01-ES020888). The content does not necessarily represent the official views of the funding agencies including the National Institute of Environmental Health Sciences or the National Institutes of Health. MM was supported by a grant from the Région Île-de-France, DIM "Problématiques transversales aux Systèmes Complexes”. CS is a Fellow of the Institut d’ Études Avancées de Nantes. GL's work is part of the project “Les lois des Dieux, des hommes et de la nature” in that Institute. The authors are grateful to Paul-Antoine Miquel, Matteo Mossio, Cheryl Schaeberle and Michael Sweeney for their critical input. The authors have no competing financial interests to declare.
Reference List
- Alberts B 2010 Model organisms and human health; Science 330 1724
- Alberts B, Bray D, Lewis J G, Raff M, Roberts K, and Watson J D 1994 Molecular Biology of the Cell (New York, NY: Garland Publishing Inc.)
- Alberts B, Johnson A, Lewis J, Raff M, Roberts K, and Walter P 2008 Molecular Biology of the Cell (London: Garland Science)
- Aon M A, Cortassa S, and O'Rourke B 2004 Percolation and criticality in a mitochondrial network; Proc. Nat. Acad. Sci. USA 101 4447-4452
- Bailly F and Longo G 2009 Biological organization and anti-entropy; Journal of Biological Systems 17 63-96
- Bailly F and Longo G 2011 Mathematics and Natural Sciences: the Physical Singularity of Life (London: Imperial College Press)
- Bak P and Sneppen K 1993 Punctuated equilibrium and criticality in a simple model of evolution; Phys. Rev. Lett. 71 4083-4086
- Barnes C, Speroni L, Quinn K, Montevil M, Saetzler K, Bode-Animashaun G, McKerr G, Georgakoudi I, Downes S, Sonnenschein C, Howard C V, and Soto A M 2014 From single cells to tissues: interactions between the matrix and human breast cells in real time; PLoS ONE 9 e93325
- Bizzarri M, Giuliani A, Cucina A, D'Anselmi F, Soto A M, and Sonnenschein C 2011 Fractal analysis in a systems biology approach to cancer; Semin. Cancer Biol. 21 175-182
- Buss L W 1987 The Evolution of Individuality (Princeton, NJ: Princeton University Press)
- Cardamone L, Laio A, Torre V, Shahapure R, and DeSimone A 2011 Cytoskeletal actin networks in motile cells are critically self-organized systems synchronized by mechanical interactions; Proc. Nat. Acad. Sci. USA 108 13978-13983
- Cottrell A 1979 The natural philosophy of engines; Contemp. Physics 20 1-10
- Darwin C 1909 The Origin of Species (New York: P.F. Collier & Son)
- Elsasser W M 1987 Reflections on a Theory of Organisms (Quebec: Orbis Publishing)
- Huang S 2009 Non-genetic heterogeneity of cells in development: more than just noise; Development 136 3853-3862
- Huh D and Paulsson J 2011 Non-genetic heterogeneity from stochastic partitioning at cell division; Nat. Genet. 43 95-100
- Jacob F 1974 The Logic of Life (New York, NY: Pantheon Books)
- Kauffman S A 1993 The Origins of Order (Oxford: Oxford University Press)
- Kupiec J J 1983 A probabilistic theory for cell differentiation, embryonic mortality and DNA C-value paradox; Specul Sci Technol 6 471-478
- Kupiec J J 2010 On the lack of specificity of proteins and its consequences for a theory of biological organization; Prog. Biophys. Mol. Biol. 102 45-52
- Leitch H G, Blair K, Mansfield W, Ayetey H, Humphreys P, Nichols J, Surani M A, and Smith A 2010 Embryonic germ cells from mice and rats exhibit properties consistent with a generic pluripotent ground state; Development 137 2279-2287
- Lenoir T 1982 The Strategy of Life: Teleology and Mechanics in Nineteenth-Century Biology (Dordrecht, Holland: D. Reidel Publishing)
- Lesne A 1998 Renormalization Methods: Critical Phenomena, Chaos, Fractal Structures (New York: Wiley)
- Longo G, Miquel P-A, Sonnenschein C, and Soto A M 2012a Is information a proper observable for biological organization?; Prog. Biophys. Mol. Biol. 109 108-14
- Longo G and Montevil M 2012 The inert vs. the living state of matter: Extended criticality, time geometry,anti-entropy - an overview; Frontiers in Physiology 3 39
- Longo G and Montevil M 2013 Extended criticality, phase spaces and enablement in biology; Chaos, Solitons & Fractals 55 64-79
- Longo G and Montevil M 2014 Perspectives on Organisms: Biological Time, Symmetries and Singularities (Berlin: Springer)
- Longo G, Montevil M, and Kauffman S 2012b No entailing laws, but enablement in the evolution of the biosphere; in Genetic and Evolutionary Computation Conference (Philadelphia: ACM)
- Luria S E 1975 36 Lectures in Biology (Cambridge: MIT Press)
- Marinov G K, Williams B A, McCue K, Schroth G P, Gertz J, Myers R M, and Wold B J 2014 From single-cell to cell-pool transcriptomes: stochasticity in gene expression and RNA splicing; Genome Res. 24 496-510
- Martin G M, Ogburn C E, Colgin L M, Gown A M, Edland S D, and Monnat R J, Jr. 1996 Somatic mutations are frequent and increase with age in human kidney epithelial cells; Hum. Mol. Genet. 5 215-221
- Minelli A 2011 Development, an open-ended segment of life; Biological Theory 6 4-15
- Montevil, M. and Mossio, M. Biological organisation as closure of constraints. Journal of Theoretical Biology. In Press 2015.
- Moore A 2012 Life defined; BioEssays 34 253-254
- Mora T and Bialek W 2011 Are biological systems poised at criticality?; J. Stat. Phys. 144 268-302
- Moss L 2003 What Genes Can't Do (Cambridge, MA: MIT Press)
- Mossio M and Moreno A 2010 Organisational closure in biological organisms; Hist. Phil. Life Sci. 32 269-288
- Muller G B 2003 Embryonic motility: environmental influences and evolutionary innovation; Evol. Dev. 5 56-60
- Nicolis G and Prigogine I 1977 Self-organization in Non-equilibrium Systems (New York: Wiley)
- Nykter M, Price N D, Aldana M, Ramsey S A, Kauffman S A, Hood L E, Yli-Harja O, and Scmulevich I 2008 Gene expression dynamics in the macrophage exhibit criticality; Proc. Nat. Acad. Sci. USA 105 1897-1900
- O'Malley M A and Dupre J 2005 Fundamental issues in systems biology; BioEssays 27 1270-1276
- Rehen S K, McConnell M J, Kaushal D, Kingsbury M A, Yang A H, and Chun J 2001 Chromosomal variation in neurons of the developing and adult mammalian nervous system; Proc. Natl. Acad. Sci U. S. A. 98 13361-13366
- Rot-Nikcevic I, Downing K J, Hall B K, and Kablar B 2007 Development of the mouse mandibles and clavicles in the absence of skeletal myogenesis; Histol. Histopathol. 22 51-60
- Rubin H 1988 Can we speak of a mechanism for malignant transformation?"; in Theories of Carcinogenesis: Facts, Fashion or Fiction? (Washington, DC: Taylor and Francis) pp 31-43
- Rubin H and Hatie C 1968 Increase in the size of chick embryo cells upon cultivation in serum-containing medium; Dev. Biol. 17 603-616
- Saçlioglu C, Pekcan Ö, and Nanjundiah V 2014 Group behaviour in physical, chemical and biological systems; J. Biosci. 39 177-189
- Salam A 1990 Unification of Fundamental Forces (Cambridge: Cambridge University Press)
- Shyer A E, Tallinen T, Nerukar N L, Wei Z, Gil E S, Kaplan D L, Tabin C J, and Mahadevan L 2013 Villification: how the gut gets its villi; Science 342 212-218
- Sonnenschein C and Soto A M 1999 The Society of Cells: Cancer and Control of Cell Proliferation (New York: Springer Verlag)
- Sonnenschein C, Soto A M, and Michaelson C L 1996 Human serum albumin shares the properties of estrocolyone-I, the inhibitor of the proliferation of estrogen-target cells; J. Steroid Biochem. Molec. Biol. 59 147-154
- Soto A M and Sonnenschein C 1985 The role of estrogens on the proliferation of human breast tumor cells (MCF-7); J. Steroid Biochem. 23 87-94
- Soto A M and Sonnenschein C 2010 Environmental causes of cancer: endocrine disruptors as carcinogens; Nat. Rev. Endocrinol. 6 363-370
- Soto A M and Sonnenschein C 2011 The tissue organization field theory of cancer: A testable replacement for the somatic mutation theory; BioEssays 33 332-340
- Soto A M and Sonnenschein C 2012 Is systems biology a promising approach to resolve controversies in cancer research?; Cancer Cell Int. 12 12
- Stebbings, H. Cell Motility. Encyclopedia of Life Sciences. 2001. Nature Publishing Group. www.els.net
- Steele M and Penny D 2010 Origins of life: Common ancestry put to the test; Nature 465 168-169
- Taniguchi Y, Choi P J, Li G W, Chen H, Babu M, Hearn J, Emili A, and Xie X S 2010 Quantifying E. coli proteome and transcriptome with single-molecule sensitivity in single cells; Science 329 533-538
- Turing A M 1950 Computing machinery and intelligence; Mind 59 433-460
- Turing A M 1952 The chemical basis of Morphogenesis; Philos Trans R Soc London [Biol] 237 37-72
- Tyagi S 2010 Genomics. E. coli, what a noisy bug; Science 329 518-519
- Ueda H, Yokota E, Kutsuna N, Shimada T, Tamura K, Shimmen T, Hasezawa S, Dolja W, and Hara-Nishimura I 2010 Myosin-dependent endoplasmic reticulum motility and F-actin organization in plant cells; Proc. Nat. Acad. Sci. USA 107 6894-6899
- van Doorn W G and van Meeteren U 2003 Flower opening and closure: a review; J. Exp. Bot. 54 1801-1812
- van Fraassen B C 1989 Laws and Symmetry (Oxford: Oxford University Press)
- Varela F G, Maturana H R, and Uribe R 1974 Autopoiesis: The organization of living systems, its characterization and a model; Biosystems 5 187-196
- Werner G 2007 Metastability, criticality and phase transitions in brain and its models; Biosystems 90 496-508
- Ying Q L, Wray J, Nichols J, Batlle-Morera L, Doble B, Woodgett J, Cohen P, and Smith A 2008 The ground state of embryonic stem cell self-renewal; Nature 453 519-523