The biological default state of cell proliferation with variation and motility, a fundamental principle for a theory of organisms
Progress in Biophysics and Molecular Biology
We propose a biological default state of proliferation with variation and motility by analogy with physics inertia. Then, quiescence requires an explanation.
Abstract
Abstract The principle of inertia is central to the modern scientific revolution. By postulating this principle Galileo at once identified a pertinent physical observable (momentum) and a conservation law (momentum conservation). He then could scientifically analyze what modifies inertial movement: gravitation and friction. Inertia, the default state in mechanics, represented a major theoretical commitment: there is no need to explain uniform rectilinear motion, rather, there is a need to explain departures from it. By analogy, we propose a biological default state of proliferation with variation and motility. From this theoretical commitment, what requires explanation is proliferative quiescence, lack of variation, lack of movement. That proliferation is the default state is axiomatic for biologists studying unicellular organisms. Moreover, it is implied in Darwin’s “descent with modification”. Although a “default state” is a theoretical construct and a limit case that does not need to be instantiated, conditions that closely resemble unrestrained cell proliferation are readily obtained experimentally. We will illustrate theoretical and experimental consequences of applying and of ignoring this principle.
Keywords: Default state, Theory, Organicism, Emergence, Mathematical symmetries, Biological organization
Table of contents
Reading time: ~42 min
- 1 Introduction
- 2 Existing biological theories
- 3 The biological default state
- 4 The usefulness of the concept of inertia and default state in biology
- 5 From inertia to operational definitions
- 6 The biological default state links ontogenesis to phylogenesis
- 7 Conclusions
- Acknowledgements:
- References
- Footnotes
The biological default state of cell proliferation with variation and motility, a fundamental principle for a theory of organisms
Abstract
The principle of inertia is central to the modern scientific revolution. By postulating this principle Galileo at once identified a pertinent physical observable (momentum) and a conservation law (momentum conservation). He then could scientifically analyze what modifies inertial movement: gravitation and friction. Inertia, the default state in mechanics, represented a major theoretical commitment: there is no need to explain uniform rectilinear motion, rather, there is a need to explain departures from it. By analogy, we propose a biological default state of proliferation with variation and motility. From this theoretical commitment, what requires explanation is proliferative quiescence, lack of variation, lack of movement. That proliferation is the default state is axiomatic for biologists studying unicellular organisms. Moreover, it is implied in Darwin’s “descent with modification”. Although a “default state” is a theoretical construct and a limit case that does not need to be instantiated, conditions that closely resemble unrestrained cell proliferation are readily obtained experimentally. We will illustrate theoretical and experimental consequences of applying and of ignoring this principle.
Keywords: default state, theory, organicism, emergence, mathematical symmetries, biological organization
1 Introduction
Biologists and philosophers have long pondered the differences between inert matter and living entities. Rather than concentrating on this type of comparison, we will mention some compelling characteristics of the living that should be taken into consideration when addressing biological phenomena. They are: agency (the capacity to initiate action[1]), normativity (the capacity of generating their own rules), individuation (the ability to change one’s own organization), the propensity to become sick, and the return to health. In this regard, Bichat referring to physical deformities stated: “Whereas monsters are still living beings, there is no distinction between normal and pathological in physics and mechanics[2]”. The distinction between the normal and the pathological holds for living beings alone”. Inspired by Canguilhem, we will add that the opposite of pathological is not “normal” but “healthy” (Canguilhem 1991). This is illustrated by the fact that individuals experiencing situs inversus totalis (heart in the right side, liver in the left side) may be perfectly healthy without being normal.
There are differences between the inert and the alive, and thus between the sciences that study them (Longo and Soto, this issue). In this regard, it is pointless to try to fit biology into physics, as one would when thinking that because a prebiotic world preceded the advent of life, life would represent a particular case of the physical “world”. In fact, scientists do not directly deal with the “real world” but with scientific disciplines constructed by the human mind to understand such a world. Hence, when we refer to the physical or biological, we are referring to the disciplines that address inert and living matter, respectively. Thus, we can only talk about the coherence between the two disciplines. That is, living matter “obeys” the laws of physics, but additional principles and observables may be necessary to understand organisms. When biology is interpreted as “extended physics” the inert state of matter can be considered as a special case or a singularity of the living state of matter. In this case, physics is biology when all organisms are ignored or dead. In science, similar conceptual transitions already exist: after Riemann, Euclidian Geometry instead of being considered the ultimate foundation of mathematics has been viewed as a special case, a singularity: Riemann’s geometry on space of no curvature (that is, curvature 0).
Before the 20th century, biologists often explicitly stated the philosophical bases for their observations, experiments and theories. Two examples of this practice are Blumenbach’s correspondence with Kant about a “formative force” (Lenoir 1982) and Darwin’s explicit mention of being influenced by Whewell (Ruse 1975). In the preceding articles of this issue we have addressed the role of theory on the choice of the observables and the construction of objectivity, particularly the founding role of Galileo’s inertia in classical mechanics. This principle represents a limit case: if no cause (a force) modifies the properties of an object, the object conserves its properties. In the rigorous mathematical sense, this is a limit or asymptotic case since there are always frictions and gravitational forces and no physical body can be exactly identified to a point-mass moving on a Euclidean straight line. For didactic purposes we use the term “default state” (borrowed from computer science) to denote a state that applies when “no action is taken”. In short, the default state is what happens when nothing is done to the intended object or system in question. Galileo’s choice of inertia as a fundamental theoretical postulate was counter-intuitive because objects present in our immediate surroundings are subject to forces that hinder the manifestation of such a state. The counter-intuitiveness of Galilean inertia is illustrated by the fact that Kepler and Leibnitz thought that the opposite was true, namely, that “The globe [meaning a planet] has a natural inertia or stillness, for which it remains at rest in every place, where it is posed alone [quoted in: (Bussotti 2015)].
The crucial point is that accepting inertia as a postulate implies that we do not need to explain uniform rectilinear motion, rather, we need to explain departures from it. The usefulness of this postulate remains uncontested in classical mechanics. In fact, 300 years after Galileo, this counter-intuitive postulate was buttressed by E Noether’s theorems; they provided a deeper understanding of inertia by justifying conservation properties of energy and momentum on the basis of time and space symmetries, respectively (van Fraassen 1989). Ever since, symmetries (and their breaking) acquired an even more fundamental role in physics.
In short, the conservation of these symmetries is based on the idea that the ‘laws’ of physics are the same at different positions and times. In spite of the advance due to Noether’s theorem, the notion of symmetries is already used in Archimedes’ law of the lever: equal weights at equal distances are in equilibrium. This article proposes a biological default state which would play a comparable useful role in organismal biology.
2 Existing biological theories
Biology has one comprehensive theory, the theory of evolution which encompasses the time-scale of phylogenesis and is based on two principles, i) reproduction with modification, and ii) natural selection. In contrast, a theory of organisms encompassing the time-scale of a life cycle has yet to be formulated. The theoretical wealth of biology is manifested by the various theories that address important but more restricted areas of biology, such as the cell theory, the chromosome theory, the germ theory of disease, etc. Among those, the one relevant to this chapter is cell theory, which postulates that cells i) are the basic unit of life, ii) are made from pre-existing cells, and iii) that organisms are made up of one or more cells and extracellular matrices, which are made by cells.
The cell theory is central to both ontogenesis and phylogenesis. Regarding the former, multicellular organisms develop from a zygote, that is at the same time a cell and an organism (Soto et al. 2008). Regarding phylogenesis, all existing living organisms are believed to have a common unicellular ancestor. Using cell theory as a starting point we postulate a biological default state as a step towards building a theory of organisms and their ontogenesis.
3 The biological default state
Let’s assume for the sake of argument that we could observe the moment that life emerged from the pre-biotic soup…. What would have been the properties of this first cell? Is it reasonable to infer that it would do pretty much the same as unicellular organisms do today? Indeed, microbiologists agree that unicellular organisms spontaneously proliferate as long as their milieu provides sufficient nutrients and appropriate ranges of pH, temperature and pressure. They would also agree that motility is commonplace in unicellular prokaryotes and eukaryotes; by motility we mean the ability to initiate movement. Motility is perhaps the most obvious instantiation of agency, i.e., the characteristic that makes the intuitive distinction between alive and inert[3].
In biology, we propose a default state of proliferation with variation and motility, which is common to all prokaryotic and eukaryotic cells, meaning all those that are unicellular organisms and those that form part of multicellular ones. In other words, paralleling the concept of inertia in classical mechanics, proliferation, variation and motility, require no explanation in biology. On the contrary, hindrances to the expression of default state, namely, proliferative quiescence, lack of variation, and lack of movement require an explanation . There is, however, a fundamental difference between the default state in mechanics and in biology. While the former is about invariance (of momentum in particular) and conservation of symmetries (of space-time), the latter is about symmetry changes.[4] These differences between theories of the inert and of the living are discussed in greater detail in Longo and Soto, this issue, and (Longo et al. 2015).
3.1 Proliferation
As mentioned above, a “default state” is a theoretical construct, a limit case, and thus does not require experimental confirmation. However, this fact does not mean that it lacks an experimental correlate. Galileo conceptualized the principle of inertia through experimentation using ramps. He gave sufficient evidence to justify the hypothesis that the Aristotelian ideas where every motion requires a moving force and where the tendency of objects is to remain at rest were wrong. Based on the experimental observations whereby Galileo was changing the influence of gravity and friction on the motion of an object, he dared to imagine a “limit” case where no forces were acting upon the object. Inertia is not a figment of the imagination; we can experience it when riding a vehicle that suddenly and forcefully stops. Similarly, in biology there are natural and experimental conditions that closely resemble unrestrained cell proliferation; these are instantiated in prokaryotes and unicellular eukaryotes, like yeast, when growing in a nutrient-rich environment, and by cells from multicellular eukaryotes when placed in culture conditions in a nutrient-rich medium. We posit that from LUCA (the Last Universal Common Ancestor) on, proliferation has been retained as the default state with the advent of multicellular organisms (metaphyta and metazoa). This conclusion is supported by the conservation of cell cycle components throughout eukaryotes (Sonnenschein and Soto 1999) and by experimental evidence (Sonnenschein and Soto 1999; Soto and Sonnenschein 1985; Sonnenschein et al. 1996; Leitch et al. 2010; Ying et al. 2008).
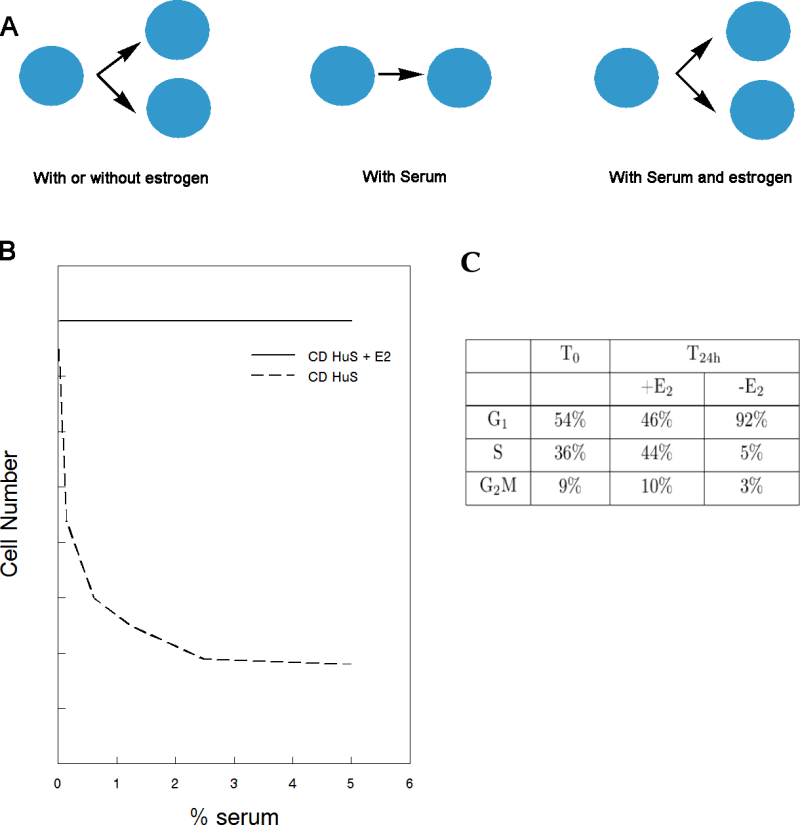
Panel A: Schematic view. Left, the blue estrogen-target cells proliferate in serumless medium regardless of the presence of estrogen. Middle, cells are constrained from proliferating by serum. Right, estrogen cancels the serum inhibition and cells proliferate.
Panel B: Schematic representation of serum inhibition. Cells proliferate maximally in the absence of serum supplement when similar numbers of estrogen-target cells are cultured in a defined medium containing nutrients. The addition of estrogen-free human serum resulted indose-dependent inhibition of cell proliferation. Addition of estrogen does increase cell numbers in serumless conditions; instead it neutralizes the inhibitory effect of serum ( ____ with estrogen, ———- without estrogen).
Panel C: Effect of serum inhibitor (recombinant serum albumin) on the cell cycle profile of estrogen target MCF7 cells at 24h. Cells in medium containing HAS are predominately arrested in G1. Almost half of the cells in media containing HSA and estrogen are undergoing DNA synthesis (S phase of the cycle).
The default state is exemplified by the behavior of estrogen-responsive cells like those in the mammary gland. When given to a sexually immature animal, estrogen will induce the growth of the ductal tree of the mammary gland. This effect was interpreted as evidence that estrogen induces the proliferation of the epithelial cells that form the ductal tree. However, when removed from the organism, these cells proliferate maximally in the absence of estrogen. Also, when estrogen-free blood serum is added to the culture medium, it induces a dose-dependent inhibition of cell proliferation, which is manifested as a cell cycle arrest in the Go-G1 phase of the cell cycle. Only after this inhibition takes place, is estrogen necessary to overcome such inhibition (Figure 1) (Sonnenschein et al. 1996); indeed, estrogen neutralizes the action of the serum-borne inhibitor. The default state of proliferation has been adopted advantageously as a fundamental principle in theories of carcinogenesis and of development (Sonnenschein and Soto 1999; Soto and Sonnenschein 2010; Minelli 2011).
3.2 Variation
Variation, an integral part of the biological default state, is readily generated with each cell division. It manifests itself as the unequal distribution of macromolecules and organelles following cell division, and it is related to the low number of these intracellular components (Huh and Paulsson 2011). Additional variation is generated by the inherent stochasticity of gene expression which leads to intrinsic cell-to-cell variation of mRNA and protein levels (Kupiec 1983; Taniguchi et al. 2010; Tyagi 2010; Marinov et al. 2014; Raj and Oudenaarden 2008). Another source of variation is generated by somatic mutations and aneuploidy, that, contrary to conventional wisdom suggesting that these events only occur in cells in a neoplastic state, were described in cells of normal mammalian organs, like kidney, liver and brain (Martin et al. 1996; Rehen et al. 2001). In this new context, aneuploidy is seen as a common and advantageous outcome; near 50% of liver cells are aneuploid and probably because of it livers are better adapted to toxic injury (Duncan et al. 2012; Rehen et al. 2005). Variation is also generated at supracellular levels of organization (Montévil et al, this issue), like during branching morphogenesis. We have referred to this supracellular source of variation when positing the framing principle of non-identical iteration of morphogenetic processes (Longo et al. 2015); Montévil et al, this issue; Montévil, Speroni and Soto, this issue).
3.3 Motility
Motility, the third component of the biological default state, encompasses intracellular, cellular, tissue and organismic non-random movements (Stebbings 2001). From gliding to swarming or swimming, the motility of microorganisms immediately suggests the idea of agency, and in fact, the organism uses these movements to migrate to more suitable environments (Jarrell and McBride 2008). To do so, they use sensors for attractants and repellents. Motility is not synonymous with locomotion. For example, plants that are attached to the ground by their roots cannot move from one location to another one, but they can make their parts move, as when growing towards a source of light. Flowers and leaves open and close in response to light (van Doorn and van Meeteren 2003), and like animal cells, can move organelles using actin and myosin (Ueda et al. 2010). In summary, like the mechanical default state, the biological one is a limit case which is theoretically derived from actual experimental observations.
4 The usefulness of the concept of inertia and default state in biology
4.1 The Hardy-Weinberg equilibrium
The introduction of inertia by Galileo, a simple and universal principle which applies to both celestial bodies like planets and stars and to terrestrial ones, like apples and cannon balls, was reformulated by Newton as the first law of motion. In addition to the indisputable founding theoretical value of such a principle in its realm of classical mechanics, it inspired evolutionary biologists to develop their own founding principle. Indeed, early in the 20th century population geneticists formulated a principle that allowed them to study the effect of several “forces”, namely mutation, selection, mate choice, on the allelic frequencies of target populations. This is the Hardy-Weinberg equilibrium principle which states “that allele and genotype frequencies in a population will remain constant from generation to generation in the absence of other evolutionary influences”. In other words, Hardy–Weinberg equilibrium describes an ideal condition against which the effects of these forces can be analyzed (Edwards 1977).
Unlike Newton’s law, the Hardy-Weinberg equilibrium does not constitute a founding principle of biology, but an epistemic tool to study the factors that will negate such equilibrium, like selection. Loosely related to this use, epidemiologists who as population geneticists deal with large populations and statistics, took from the latter the idea of a null hypothesis representing the possible outcome that chance is only responsible for the observed results. Again, the epistemic value of these tools is that it fixes a “no-change” hypothetical condition against which to study change.
4.2 The Zero Force Evolutionary Law
Quite recently, some evolutionary biologists criticized the Hardy-Weinberg equilibrium when taken as a founding principle. More precisely, Brandon and McShea stated that quite to the contrary of the stasis represented by Hardy-Weinberg, their view of “the zero-force evolutionary law” is the constitutive tendency for diversity and complexity to increase (Brandon and McShea 2012). In contraposition to the Hardy-Weinberg equilibrium, by adopting the zero-force evolutionary law what requires explanation is stasis. By claiming that the “…default condition of evolutionary systems is change, and change of a particular sort—increase of diversity and complexity”, these authors elevate their “zero-force evolutionary law” to a natural condition, that is, a situation for which there is empirical evidence (Brandon and McShea 2012; Gouvêa 2015). We are now full circle back to the point where we described inertia as a limit case derived from empirical evidence. Additionally, this zero-force evolutionary law, like the biological default state, is about change.
4.3 The Zero Force Evolutionary Law: a consequence of the default state
We consider that the “zero-force evolutionary law” is not the biological first law. Instead, the “zero-force evolutionary law” is the consequence of the biological default state, which is the generator of intrinsic variation[5]. The general tendency of biological evolution towards an increase of the average complexity is compatible with the fact that some species have lost appendages, structures or organs and become less complex under various complexity measurements. We consider this fact as a consequence of a more general phenomenon, which was proposed by S.-J. Gould (Gould 1996) and closely analyzed in (Bailly and Longo 2009) and (Longo and Montévil 2014). Gould proposed a “left wall” of minimal organismal complexity, such as that of bacteria, beyond which life is not possible (Figure 2).
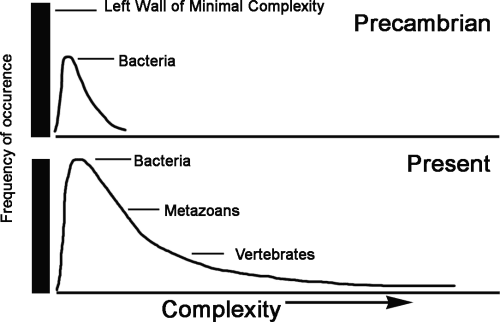
From this initial stage (proliferation with variation), the expression of the default state results in the increase of the biomass while creating diversity. Like a gas exploding against a wall, the diffusion of the biomass generated by the default state is asymmetric, resulting in increased average complexity. This means that there is no need for any sort of evolutionary pressure towards higher complexity. Indeed, the curve proposed by Gould as a preliminary mathematical description of this spreading of life may be fully reconstructed with a diffusion equation that includes the dynamics of asymmetric boundary conditions (the left wall)(Bailly and Longo 2009; Longo and Montévil 2014). This is done by assuming that evolution follows a variability law, which is a consequence of the default state.. As a consequence of the original asymmetry and the default state, complexity can only increase on average, with no need to assume this increase as a principle. In this way, two very simple assumptions produce a strong consequence..[6] Indeed, this structure of reasoning also applies to the evolution of other organismal quantities, such as body mass, as long as the ancestor organism has a low value for this quantity when compared to their descendants. Thus, the “diffusion” following from the instantiation of the default state will result in an average increase of the considered quantity over evolution. In particular, the default state justifies the diffusion equation used to model the evolution (and overall increase) of the mass of mammals in combination with a selective pressure against this increase (Clauset and Redner 2009). It follows that the same reasoning would apply mutatis mutandis to different measures of complexity, provided they follow the above assumptions. Again, the default state principle has more generality than the “zero-force evolutionary law”; meaning that the latter may be understood as a consequence of the former.
5 From inertia to operational definitions
Given that evolutionary biologists used the principle of inertia in the first decade of the 20th century, why is it that organismal biologists have yet to develop comparable theoretical constructs? We attribute this lack of theoretical thinking in organismal biology to the belief expressed by many biologists in the first half of the 20th century that facts “speak for themselves” (see Perret et al in this issue), and later, to the adoption of the mathematical theory of information without critical examination. This brought the metaphorical use of the concepts of information, program and signal to biology hindering its progress (Longo et al. 2012). Regarding the former, organismal biologists tend to believe that they observe the “real world” and thus that data are objective. Contrary to this belief, data are theory laden, and thus one should examine the hidden philosophical content of “data”. Another important factor in this discussion is that, lacking global theories, operational thinking plus dubious common-sense beliefs become the substitute for theories. In operationalism, scientific terms are defined by the experimental operations which determine their applicability (Hull 1968).
5.1 The operational origins of hormones and growth factors
Surgical removal of the gonads results in atrophy of the accessory sex organs (uterus, prostate). This non-controversial fact prompted the search for “factors” secreted by gonads that made the accessory organs grow in size, due to an increase of their cell number and in the deposition of extracellular matrix. Administration of gonadal extracts resulted in the reversal of this atrophy and in due turn, the substances that produced these trophic effects were identified. They were named “hormones”, and were defined operationally as the substances that, in their bioassays, induced the growth of the target organs. The operational nature of this definition was soon forgotten and it became a “fact” that hormones directly stimulate proliferation., Despite evidence to the contrary, this notion remains engrained among specialists (Sonnenschein and Soto 1999).
The concept of “growth factor” appeared in the early 20th century when biologists, having succeeded in propagating bacteria in medical laboratories using meat broth and other complex extracts and body fluids, turned to the study of bacterial nutrition. Any substance that improved bacterial propagation was called a “growth factor”. In modern microbiology textbooks, growth factors are defined as substances required in small amounts by unicellular organisms because they fulfill specific roles in the biosynthesis of the organism’s own components. A growth factor is necessary when a metabolic pathway is missing or is blocked. In this context growth factors are purines and pyrimidines, amino acids and vitamins.
At the time when several groups attempted to develop methods to culture cells isolated from metazoan organisms, research on bacterial metabolism and nutrition was flourishing. Among those groups, Margaret and Warren H. Lewis at Johns Hopkins University empirically created artificial conditions of life while wishing to have control over these cells. For the Lewises, cells were not agents. Instead, they thought that in order to grow the cells needed to be “stimulated” to proliferate as if they were as passive as inert objects. In hindsight, we now know that when freshly isolated cells fail to thrive it is not due to them being quiescent but because they die. Slowly but inexorably, the operational concept of “growth factor” became established within the field of tissue culture as a specific “signal” to induce a passive cell to proliferate (Sonnenschein et al. 2013).
The idea of a “program” in biology reinforced the view that cells need to receive “information” or “signals” in order to proliferate and to move. When applying this thinking to the initial cell at the beginning of life what or who would be the purveyor of such stimuli? From our perspective, cell culture represents a state of de-emergence, whereby the cells that form part of an organism are “liberated” from the constraints imposed by that organism. Under extra-organismic (in culture) conditions, these cells regain properties that mimic those of the unicellular organisms from which the multi-celled organism eventually evolved. This brings up the relevance of placing cell and tissue culture under an evolutionary perspective. The pioneers of tissue culture failed to apply evolutionary theory when venturing into quasi-artificial life (Maienschein 1983). In hindsight, this was a squandered opportunity to recognize that in the quasi-artificial life of the culture flask, metazoan cells behave as unicellular organisms, and thus exert their constitutive ability to proliferate and move, properties that enabled the LUCA to generate all the diversity of life on earth that we recognize today.
5.2 From operational definitions to “the law of the land”
As mentioned above, microbiologists accept as fact that unicellular organisms constitutively proliferate in the presence of nutrients (proliferation is their default state). Obviously, cells in multicellular organisms do not exhibit unconstrained cell proliferation. Below we transcribe the standard explanation for this difference from a widely used textbook. “Unicellular organisms tend to grow and divide as fast as they can, and their rate of proliferation depends largely on the availability of nutrients in the environment. The cells of a multicellular organism, however, divide only when the organism needs more cells. Thus, for an animal cell to proliferate, it must receive stimulatory extracellular signals, in the form of mitogens, from other cells, usually its neighbors. Mitogens overcome intracellular braking mechanisms that block progress through the cell cycle.”(Alberts et al. 2014)
From the above analysis about inertia and a biological default state, what exactly is objectionable in the just quoted textbook account of this difference? The quotation acknowledges that unicellular organisms have proliferation as their default state. Next, it moves to multicellular organisms and, it states the obvious: that cells in multicellular organisms do not proliferate despite plenty of nutrients being available. From there, while using common sense, the sense that Galileo systematically disregarded, the quotation claims as a fact that animal cells are quiescent and need stimuli, i.e. signals to proliferate. This option implies a reversal of the default state taking place with the advent of multicellularity. However, no explanation is given about the acknowledged fact that metaphyta conserved proliferation as the default state, or that the cell cycle components are conserved through evolution; altogether, these pieces of evidence strongly suggest that there was no change of default state in the cells of multicellular organisms. The concept that the default state could be constrained in animals, namely, that an additional layer of regulation emerged during the advent of multicellularity, was not contemplated by the authors of the textbook referred to above.
Since the introduction of the concept of a biological default state operating in all cells (Soto and Sonnenschein 1991), researchers dealing with the phenomenon of lymphocyte quiescence found that quiescence is an induced state, namely that proliferation is actively constrained. Separately, other researchers concluded that embryonic stem cells proliferate constitutively, a phenomenon they called “ground state” (Ying et al. 2008; Leitch et al. 2010). In both cases, proliferation as a default state was interpreted as a peculiarity of the particular experimental model being investigated. The absence of a bold attempt to generalize these findings to all cells is probably due to a dominant perception among biologists that there are neither laws nor rules in biology. Finally, and most fundamentally, in the absence of a global theoretical framework that constructs objectivity and determines the proper observables, organismal biology appears as less intelligible given that new results create more contradictions that happily coexist and are never discarded.
6 The biological default state links ontogenesis to phylogenesis
The biological default state is a founding principle upon which a theory of organisms and of their ontogenesis can be constructed. It takes into consideration the agency of organisms manifested as the constitutive ability to reproduce and generate movement. Equally important, the biological default state ties the source of variation together with its transmission at each proliferative event. Each cell division thus represents a symmetry change that generates two non-identical daughter cells.
A founding principle for a theory of organisms that addresses ontogenesis needs to be compatible with the theory of evolution, which addresses phylogenesis. Below we address three points in common between these theories, namely, constitutive reproduction/ proliferation, variation and historicity.
6.1 Darwin’s limit case and the default state
In the Origin of Species, Darwin stated: “…There is no exception to the rule that every organic being naturally increases at so high a rate, that, if not destroyed, the earth would soon be covered by the progeny of a single pair” (Darwin 1859). According to Darwin’s theory, reproduction is linked to modification: in his own words, “descent with modification”. Reproduction with variation is intrinsic to organisms regardless of whether they are unicellular or multicellular (Sonnenschein and Soto 1999; Soto and Sonnenschein 2011). Darwin’s narrative implies that reproduction with variation is a default state and he describes it as a limit case. In fact, because reproduction and proliferation are the same event in asexual reproduction of unicellular organisms, this default state represents a common postulate for the theories of evolution and organisms.
6.2 Change, symmetry breaks, and historicity
The theory of evolution addresses the generation of incessant change (variation in our words, modification in Darwin’s) upon which natural selection operates; the result is phenotypic diversity. The incessant changes of life processes may be analyzed as extended critical transitions (Bailly and Longo 2011; Longo and Montévil 2014). Under our theoretical approach, throughout its ontogeny, an organism may be understood as being in a permanent transition with all the main signatures of criticality, such as changes of symmetries and the formation of a new global structure (Longo et al. 2015). In an organism, each cell division changes local symmetries because each of those divisions forces new local and global correlations. These changes yield variability and adaptability to organisms. In the context of evolution, the advent of new functions and organs are additional examples of symmetry changes.
Far-from-equilibrium, self-organizing physical systems have been used as a starting point to understand complex biological organization. These physical systems are understood by the analysis of their instantaneous flows. Indeed, the shape of a flame can be calculated from the flows of matter that go through it, whereas the shape of an organism cannot. Far from equilibrium systems appear spontaneously and can be analyzed independently. In contrast, organisms are not spontaneous but historical; that is, they are a consequence of the reproductive activity of a pre-existing organism. Organization cannot be deduced from flows operating within and upon organisms; instead, understanding biological organization requires a historical analysis, and this applies to the time-scale of ontogenesis as well as the one of phylogenesis (Longo et al. 2015).
Finally, the recently proposed “zero-force evolutionary law” (Brandon and McShea 2012; Gouvêa 2015), namely the constitutive tendency for diversity and complexity to increase throughout evolution is not a default state or principle, but a derived property of the biological default state. The zero-force evolutionary law stresses increasing complexity and diversity. As we mentioned above in reference to Gould’s work, this tendency may be seen as a consequence of i) the agency of living matter instantiated by the biological default state of proliferation with variation and motility, and of ii) natural selection, once this increase of diversity and complexity is analyzed in the global terms of an asymmetric diffusion from the least (bacterial) complexity.
7 Conclusions
The view proposed herein is anchored in the radical materiality of the living, whereby it is impossible to dissociate the actual materials from which living organisms are made of from the functions these organisms fulfill. This view is inimical to the strong dualism implied by the notion of program and information which manifests itself in the independence of the software from its material substrate, the hardware. On the contrary, cells can only be obtained by the proliferation of pre-existing cells which are made up of chemicals of a precise composition. Paraphrasing the epigraph by Paul Weiss, a theory of organisms should be based on the notions that all cells come from pre-existing cells, and that every biological organization comes from preexisting organization. These tenets rule out both the spontaneous generation of living matter and of biological organization. Instead, the cell is an agent and an individual endowed with normative capacity, even when residing in a multicellular organism. Indeed, every organism was once a cell, and in multicellular organisms undergoing embryonic development, the zygote resulting from the union of a female and male gamete is both a cell and an organism. Thus, organisms are the consequence of the inherent variability generated by proliferation, motility and self-organization. Their morphogenesis would then be the result of the default state plus physical constraints, like gravity, and those generated and imposed by the organism itself, such as physical ones like muscular tension, tissue rigidity and compliance, and chemical ones such as the molecular particularities of amino-acids, proteins and nucleic acids.
Acknowledgements:
This work was conducted as part of the research project “addressing biological organization in the post-genomic era” which is supported by the International Blaise pascal Chairs, Région Île-de-France. Additional support to AMS was provided by Grant R01ES08314 (P.I. AMS) from the U. S. National Institute of Environmental Health Sciences. Maël Montévil is supported by Labex Who am I?, laboratory of Excellence No. ANR-11-LABX-0071. The funders had no role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript. The authors are grateful to Cheryl Schaeberle for her critical input. The authors have no competing financial interrests to declare.
References
- Alberts, B., Johnson, A., Lewis, J., Morgan, D., Raff, M., Roberts, K., Walter, P. 2014. Molecular Biology of the Cell. 6th ed. Garland Science, New York.
- Bailly, F., Longo, G. 2009. Biological organization and anti-entropy. Journal of Biological Systems 17, 63-96.
- ——— 2011. Mathematics and Natural Sciences: the Physical Singularity of Life. Imperial College Press, London.
- Brandon, R.N., McShea, D.W. 2012. Four solutions to four puzzles. Biology and Philosophy 27, 737-744.
- Burge, T. 2009. Primitive agency and natural norms. Philosophy and Phenomenological Research 79, 251-278.
- Bussotti, P. 2015. The complex itinerary of Leibniz’s planetary theory: physical convictions, metaphysical principles and Keplerian inspiration. Birkhäuser, Basel Switzerland.
- Canguilhem, G. 1991. The Normal and the Pathological. Zone Books, New York.
- ——— 2008. Knowledge of Life. Fordham University Press, New York.
- Clauset, A., Redner, S. 2009. Evolutionary model of species body mass diversification. Phys. Rev. Lett. 102, 038103.
- Darwin, C. 1859. On the Origin of Species. 1st ed. Clowes and Sons, London.
- Duncan, A.W., Hanlon Newell, A.E., Bi, W., Finegold, M.J., Olson, S.B., Beaudet, A.L., Grompe, M. 2012. Aneuploidy as a mechanism for stress-induced liver adaptation. J. Clin. Invest. 122, 3307-3315.
- Edwards, A.W.F. 1977. Foundations of Mathematical Genetics. Cambridge University Press, Cambridge.
- Gould, S.J. 1996. Full House. Three Rivers Press, New York.
- Gouvêa, D.Y. 2015. Explanation and the evolutionary first law(s). Philosophy of Science 82, 363-382.
- Huh, D., Paulsson, J. 2011. Non-genetic heterogeneity from stochastic partitioning at cell division. Nat. Genet. 43, 95-100.
- Hull, D.L. 1968. The operational imperative: sense and nonsense in operationism. Systemic Zoology 17, 438-457.
- Jarrell, K.F., McBride, M.J. 2008. The surprisingly diverse ways that prokaryotes move. Nat. Rev. Microbiol. 6, 466-476.
- Kupiec, J.J. 1983. A probabilistic theory for cell differentiation, embryonic mortality and DNA C-value paradox. Specul Sci Technol 6, 471-478.
- Leitch, H.G., Blair, K., Mansfield, W., Ayetey, H., Humphreys, P., Nichols, J., Surani, M.A., Smith, A. 2010. Embryonic germ cells from mice and rats exhibit properties consistent with a generic pluripotent ground state. Development 137, 2279-2287.
- Lenoir, T. 1982. The Strategy of Life: Teleology and Mechanics in Nineteenth-Century Biology. D. Reidel Publishing, Dordrecht, Holland.
- Longo, G., Miquel, P.-A., Sonnenschein, C., Soto, A.M. 2012. Is information a proper observable for biological organization? Prog. Biophys. Mol. Biol. 109, 108-14.
- Longo, G., Montévil, M. 2014. Perspectives on Organisms: Biological Time, Symmetries and Singularities. Springer, Berlin.
- Longo, G., Montévil, M., Sonnenschein, C., Soto, A.M. 2015. In search of principles for a theory of organisms. J. Biosci. 40, 955-968.
- Longo, G. & Soto, A.M. 2016, this issue, Why do we need theories?, Progress in Biophysics and Molecular Biology, Available online 4 July 2016, ISSN 0079-6107, doi: 10.1016/j.pbiomolbio.2016.06.005
- Maienschein, J. 1983. Experimental biology in transition: Harrison’s Embryology 1885-1910. Stud. Hist. Bio. 107-127.
- Marinov, G.K., Williams, B.A., McCue, K., Schroth, G.P., Gertz, J., Myers, R.M., Wold, B.J. 2014. From single-cell to cell-pool transcriptomes: stochasticity in gene expression and RNA splicing. Genome Res. 24, 496-510.
- Martin, G.M., Ogburn, C.E., Colgin, L.M., Gown, A.M., Edland, S.D., Monnat, R.J., Jr. 1996. Somatic mutations are frequent and increase with age in human kidney epithelial cells. Hum. Mol. Genet. 5, 215-221.
- Minelli, A. 2011. Development, an open-ended segment of life. Biological Theory 6, 4-15.
- Miquel, P.-A., Hwang, S.-Y 2016, this issue. From physical to biological individuation, Progress in Biophysics and Molecular Biology, Available online 16 July 2016, ISSN 0079-6107, doi: 10.1016/j.pbiomolbio.2016.07.002
- Montévil, M., Mossio, M., Pocheville, A. & Longo, G. 2016, this issue. Theoretical principles for biology: Variation, Progress in Biophysics and Molecular Biology, Available online 13 August 2016, ISSN 0079-6107, doi: 10.1016/j.pbiomolbio.2016.08.005
- Montévil, M., Speroni, L., Sonnenschein, C., Soto, A.M. 2016, this issue. Modeling mammary organogenesis from biological first principles: Cells and their physical constraints, Progress in Biophysics and Molecular Biology, Available online 18 August 2016, ISSN 0079-6107, doi: 10.1016/j.pbiomolbio.2016.08.004
- Moreno, A., Mossio, M. 2015. Biological Autonomy: A Philosophical and Theoretical Enquiry. Springer, New York.
- Perret, N. & Longo, G. 2016, this issue. Reductionist perspectives and the notion of information, Progress in Biophysics and Molecular Biology, Available online 22 July 2016, ISSN 0079-6107, doi: 10.1016/j.pbiomolbio.2016.07.003
- Raj, A., Oudenaarden, A. 2008. Nature, nurture, or chance: stochastic gene expression and its consequences. Cell 135, 216-226.
- Rehen, S.K., McConnell, M.J., Kaushal, D., Kingsbury, M.A., Yang, A.H., Chun, J. 2001. Chromosomal variation in neurons of the developing and adult mammalian nervous system. Proc. Natl. Acad. Sci U. S. A. 98, 13361-13366.
- Rehen, S.K., Yung, Y.C., McCreight, M.P., Kaushal, D., Yang, A.H., Almeida, B.S., Kingsbury, M.A., Cabral, K.M., McConnell, M.J., Anliker, B., Fontanoz, M., Chun, J. 2005. Constitutional aneuploidy in the normal human brain. J. Neurosci. 25, 2176-2180.
- Ruse, M. 1975. Darwin’s debt to philosophy: an examination of the influence of the philosophical ideas of John F.W. Hershel and William Whewell on the development of Charles Darwin’s theory of evolution. Stud. Hist. Phil. Sci. 6, 159-181.
- Sonnenschein, C., Lee, D., Nguyen, J., Soto, A.M. 2013. Unanticipated trends stemming from the history of cell culture: Vitalism in 2012?, in: Vitalism and the Scientific Image in Post-Enlightenment Life Science, 1800-2010 Normandin, S., Wolfe, C., (Eds.),Springer, pp. 293-310.
- Sonnenschein, C., Soto, A.M. 1999. The Society of Cells: Cancer and Control of Cell Proliferation. Springer Verlag, New York.
- Sonnenschein, C., Soto, A.M., Michaelson, C.L. 1996. Human serum albumin shares the properties of estrocolyone-I, the inhibitor of the proliferation of estrogen-target cells. J. Steroid Biochem. Molec. Biol. 59, 147-154.
- Soto, A.M., Sonnenschein, C. 1985. The role of estrogens on the proliferation of human breast tumor cells (MCF-7). J. Steroid Biochem. 23, 87-94.
- ——— 1991. Regulation of cell proliferation: the negative control perspective. Ann. NY Acad. Sci. 628, 412-418.
- ——— 2010. Environmental causes of cancer: endocrine disruptors as carcinogens. Nat. Rev. Endocrinol. 6, 363-370.
- ——— 2011. The tissue organization field theory of cancer: A testable replacement for the somatic mutation theory. BioEssays 33, 332-340.
- Soto, A.M., Sonnenschein, C., Miquel, P.-A. 2008. On physicalism and Downward Causation in Developmental and Cancer Biology. Acta Biotheoretica 56, 257-274.
- Stebbings, H. 2001. Cell Motility. Encyclopedia of Life Sciences. Nature Publishing Group. Ref Type: Electronic Citation
- Taniguchi, Y., Choi, P.J., Li, G.W., Chen, H., Babu, M., Hearn, J., Emili, A., Xie, X.S. 2010. Quantifying E. coli proteome and transcriptome with single-molecule sensitivity in single cells. Science 329, 533-538.
- Tyagi, S. 2010. Genomics. E. coli, what a noisy bug. Science 329, 518-519.
- Ueda, H., Yokota, E., Kutsuna, N., Shimada, T., Tamura, K., Shimmen, T., Hasezawa, S., Dolja, W., Hara-Nishimura, I. 2010. Myosin-dependent endoplasmic reticulum motility and F-actin organization in plant cells. Proc. Nat. Acad. Sci. USA 107, 6894-6899.
- van Doorn, W.G., van Meeteren, U. 2003. Flower opening and closure: a review. J. Exp. Bot. 54, 1801-1812.
- van Fraassen, B.C. 1989. Laws and Symmetry. Oxford University Press, Oxford.
- Ying, Q.L., Wray, J., Nichols, J., Batlle-Morera, L., Doble, B., Woodgett, J., Cohen, P., Smith, A. 2008. The ground state of embryonic stem cell self-renewal. Nature 453, 519-523.
Footnotes
-
These definitions of agency, normativity and individuality are chosen because they are brief and broadly useful. They have been discussed more extensively (Burge 2009; Moreno and Mossio 2015) and PA Miquel this issue) ↩
-
Quoted by (Canguilhem 2008) page 90↩
-
Inert definition: having no inherent power of action, motion, or resistance (http://dictionary.reference.com/browse/inert). ↩
-
Theoretical symmetries are transformations that do not change the intended aspect of an object (or mathematically of an equation). For example, the equation of classical gravitation does not depend on the time or location of the objects considered, only their mass and relative distance matter. Theoretical symmetries have a fundamental role in physics making possible its formalization by using mathematical tools and concepts (van Fraassen 1989; Bailly and Longo 2011; Montevil et al. this issue).↩
-
It is worth noting that the authors of this Chapter independently arrived at the conclusion that the “zero force evolutionary law” is not a principle. While Soto and Sonnenschein proposed that the generation of variation by the default state is the condition of possibility for the zero-force evolutionary law, Longo and Montévil derived the increasing diversity and complexity in evolution from the asymmetric random diffusion principle they postulated (Longo and Montévil 2014), p229).”↩
-
In (Bailly and Longo 2009) a detailed, yet preliminary, measure of organismal complexity is formalized, which refines Gould’s informal scheme, and set the basis for the proposal of a “hallmark” of cancer in (Longo et al. 2015). As a matter of fact, cancer seems to be the only pathology where decreasing functionality (of organs) is correlated to increasing complexity (of tissues: folding, fractal structures, increasing number of lumena). ↩